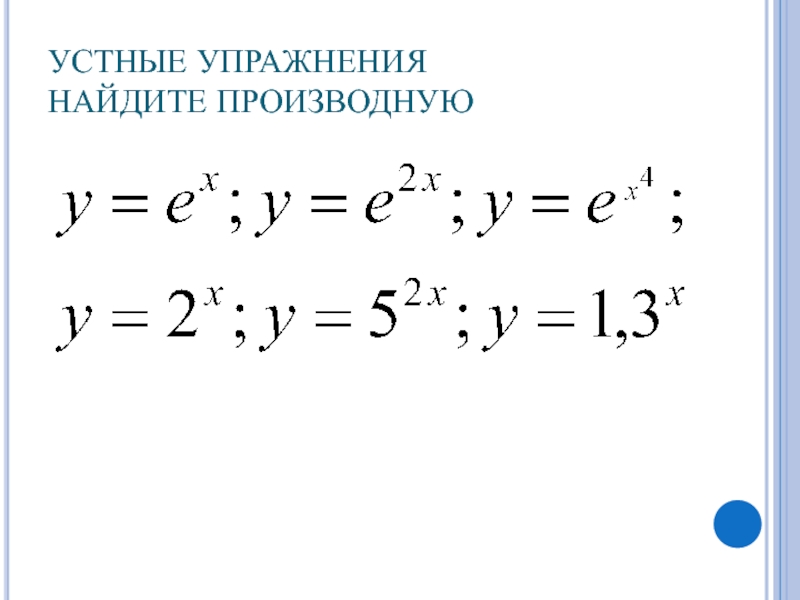Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная и первообразная показательной, логарифмической и степенной функции
Содержание
- 1. Производная и первообразная показательной, логарифмической и степенной функции
- 2. НАЧИНАТЬ ИССЛЕДОВАНИЯ МОЖНО ПО-РАЗНОМУ... ЕСТЬ ИСТИНЫ… НАИБОЛЕЕ
- 3. ЦЕЛЬ УРОКАПОВТОРИТЬ ОБОБЩИТЬЗАКРЕПИТЬ ЗНАНИЯ ПОДГОТОВИТЬСЯ К КОНТРОЛЬНОЙ РАБОТЕ
- 4. ПОВТОРЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА1.Что такое число е? 2.
- 5. ВЫБРАТЬ ИЗ ПРЕДЛОЖЕННЫХ ФУНКЦИЙ 1.ПОКАЗАТЕЛЬНЫЕ 2.ЛОГАРИФМИЧЕСКИЕ 3.СТЕПЕННЫЕ
- 6. ПОКАЗАТЕЛЬНЫЕ 1,3,4,10,12,15. ЛОГАРИФМИЧЕСКИЕ 6,9,11,13. СТЕПЕННЫЕ
- 7. Нам знакомы функцииПрямаяПараболаКубическая параболаГипербола
- 8. Показатель р = 2n – четное натуральное
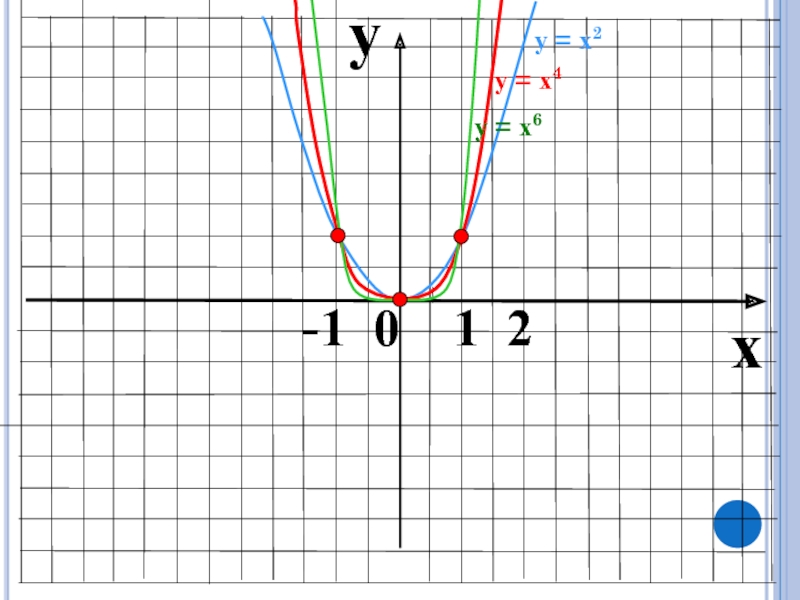
- 9. yx -1 0 1 2у = х2 у = х6у = х4
- 10. Показатель р = 2n-1 – нечетное
- 11. yx -1 0 1 2у = х3 у = х7у = х5
- 12. Показатель р = – (2n-1), где n
- 13. 0Показатель р – положительное действительное нецелое число1хуу
- 14. yx -1 0 1 2у = х0,5
- 15. yx -1 0 1 2
- 16. 0Показатель р – отрицательное действительное нецелое число1хуу
- 17. yx -1 0 1 2
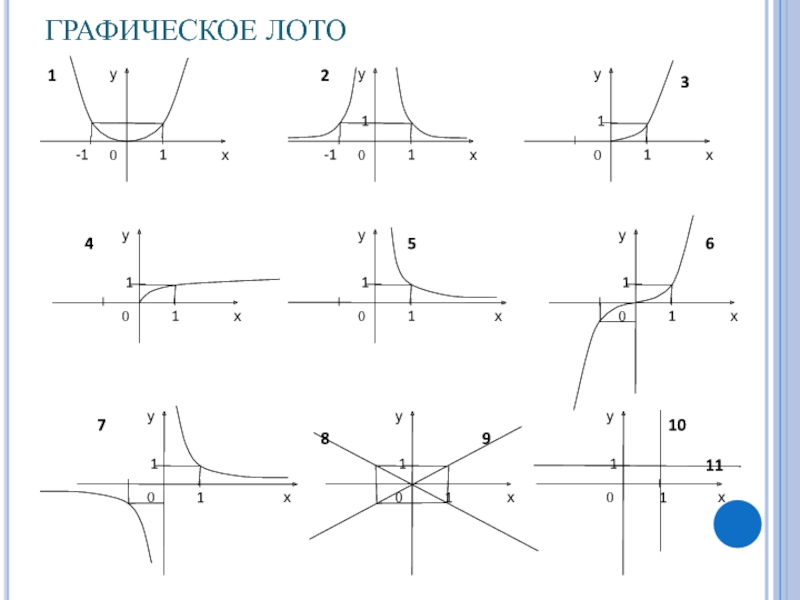
- 18. ГРАФИЧЕСКОЕ ЛОТО
- 19. ГРАФИЧЕСКОЕ ЛОТО. ОТВЕТЫ. 1 вариант9, 5, 3,
- 20. ТАБЛИЦА ПРОИЗВОДНЫХ И ПЕРВООБРАЗНЫХ
- 21. УСТНЫЕ УПРАЖНЕНИЯ НАЙДИТЕ ПРОИЗВОДНУЮ
- 22. УСТНЫЕ УПРАЖНЕНИЯ НАЙДИТЕ ПРОИЗВОДНУЮ
- 23. УСТНЫЕ УПРАЖНЕНИЯ НАЙДИТЕ ПЕРВООБРАЗНУЮ
- 24. САМОСТОЯТЕЛЬНАЯ РАБОТА1 вариант2 вариант
- 25. ОТВЕТЫ 1 вариант2 вариантШкала оценок«5» - 6 заданий«4» - 5 заданий«3» - 4 заданий«2» - 0-3заданий
- 26. НАЙДИТЕ ТАНГЕНС УГЛА НАКЛОНА ГРАФИКА ФУНКЦИИ В ТОЧКЕ Х=0.
- 27. АЛГОРИТМ НАХОЖДЕНИЯ ПРОМЕЖУТКОВ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ
- 28. НАЙДИТЕ ПРОМЕЖУТКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ
- 29. НАЙДИТЕ ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ, ОГРАНИЧЕННОЙ ЛИНИЯМИ. 1. 2.
- 30. СОСТАВЬТЕ УРАВНЕНИЕ КАСАТЕЛЬНОЙ В ТОЧКЕ Х=1
- 31. ТЕСТ.
- 32. ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА
- 33. ИТОГ УРОКА
- 34. Скачать презентанцию
НАЧИНАТЬ ИССЛЕДОВАНИЯ МОЖНО ПО-РАЗНОМУ... ЕСТЬ ИСТИНЫ… НАИБОЛЕЕ УДОБНЫЙ ПУТЬ К КОТОРЫМ СТАНОВИТСЯ ИЗВЕСТНЫМ ЛИШЬ ПОСЛЕ ТОГО, КАК МЫ ИСПРОБУЕМ ВСЕ ПУТИ. НА ПУТИ К ИСТИНЕ МЫ ПОЧТИ ВСЕГДА ОБРЕЧЕНЫ СОВЕРШАТЬ ОШИБКИ
Слайды и текст этой презентации
Слайд 1ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ:
«Производная и первообразная показательной, логарифмической и степенной
функции»
Слайд 2НАЧИНАТЬ ИССЛЕДОВАНИЯ МОЖНО ПО-РАЗНОМУ...
ЕСТЬ ИСТИНЫ…
НАИБОЛЕЕ УДОБНЫЙ ПУТЬ К
КОТОРЫМ СТАНОВИТСЯ ИЗВЕСТНЫМ ЛИШЬ ПОСЛЕ ТОГО, КАК МЫ ИСПРОБУЕМ ВСЕ
ПУТИ.НА ПУТИ К ИСТИНЕ МЫ ПОЧТИ ВСЕГДА ОБРЕЧЕНЫ СОВЕРШАТЬ ОШИБКИ
Денни Дидро
ЭПИГРАФ К УРОКУ
Denis Diderot
1713 - 1784
«УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В ЗНАНИИ, НО И В УМЕНИИ ПРИМЕНЯТЬ ЗНАНИЯ НА ПРАКТИКЕ»
АРИСТОТЕЛЬ
Слайд 4ПОВТОРЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
1.Что такое число е?
2. Какая функция называется
показательной?
3.Какая функция называется логарифмической?
4.Какая функция называется степенной?
Слайд 6ПОКАЗАТЕЛЬНЫЕ
1,3,4,10,12,15.
ЛОГАРИФМИЧЕСКИЕ
6,9,11,13.
СТЕПЕННЫЕ
2,8,14,16.
Шкала оценок
«5» - без ошибок
«4» - 1-2 ошибки
«3» - 3-4
ошибки
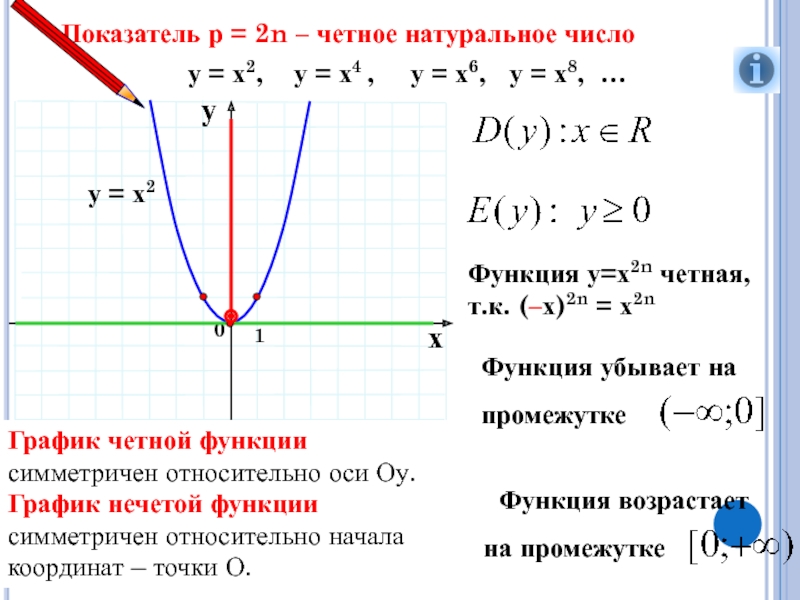
Слайд 8Показатель р = 2n – четное натуральное число
1
0
х
у
у = х2,
у = х4 , у =
х6, у = х8, …у = х2
Функция у=х2n четная,
т.к. (–х)2n = х2n
Область определения функции –
значения, которые может принимать переменная х
Область значений функции –
множество значений,
которые может принимать
переменная у
График четной функции симметричен относительно оси Оу.
График нечетой функции симметричен относительно начала координат – точки О.
Слайд 10Показатель р = 2n-1 – нечетное натуральное число
1
х
у
у =
х3, у = х5, у =
х7, у = х9, …у = х2
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
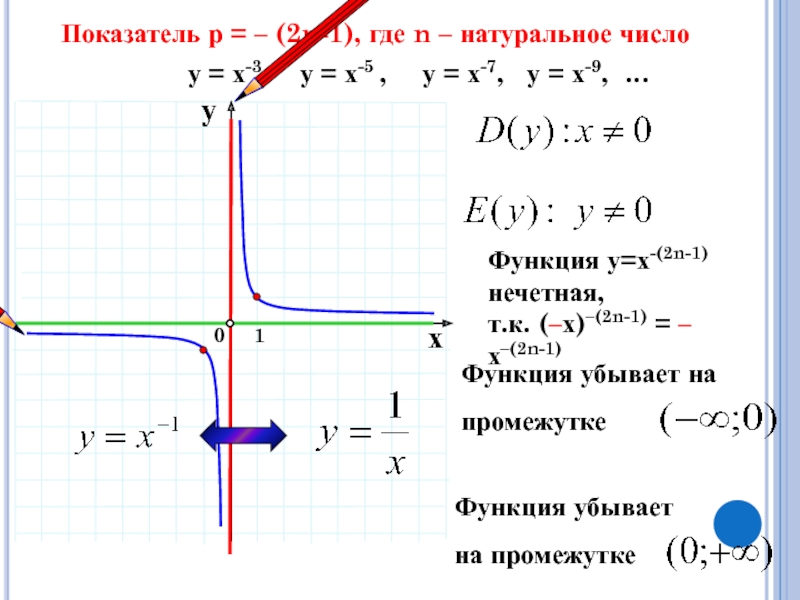
Слайд 12Показатель р = – (2n-1), где n – натуральное число
1
0
х
у
у
= х-3, у = х-5 ,
у = х-7, у = х-9, …Функция у=х-(2n-1) нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Слайд 130
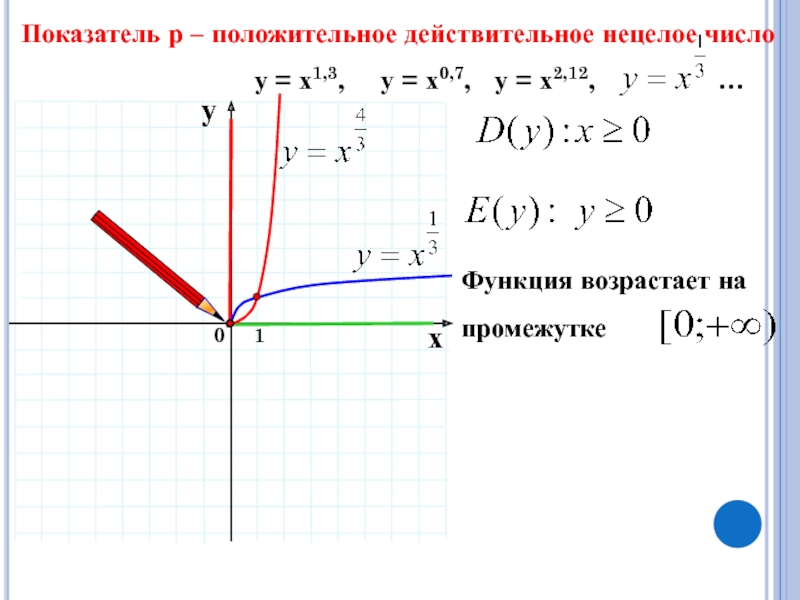
Показатель р – положительное действительное нецелое число
1
х
у
у = х1,3,
у = х0,7, у = х2,12,
…
Слайд 160
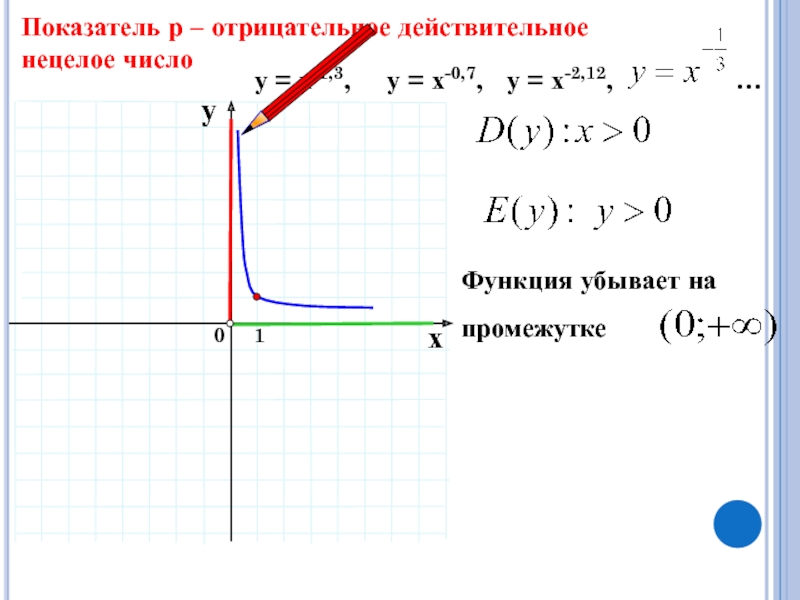
Показатель р – отрицательное действительное
нецелое число
1
х
у
у = х-1,3,
у = х-0,7, у = х-2,12,
…
Слайд 19ГРАФИЧЕСКОЕ ЛОТО. ОТВЕТЫ.
1 вариант
9, 5, 3, 4, 2, 1, 6,
7, 1, 11, 4, 3.
2 вариант
8, 5, 4, 3,
1, 2, 7, 6, 3, 10, 4, 6.Шкала оценок
«5» - 11-12 заданий
«4» - 8-10 заданий
«3» - 6-7 заданий
«2» - 0-5заданий
Слайд 25ОТВЕТЫ
1 вариант
2 вариант
Шкала оценок
«5» - 6 заданий
«4» - 5
заданий
«3» - 4 заданий
«2» - 0-3заданий
Слайд 27АЛГОРИТМ НАХОЖДЕНИЯ ПРОМЕЖУТКОВ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ
1. Найти производную функции.
2.
Приравнять производную к нулю.
3. Исследовать производную на промежутках.
4. Сделать вывод.
