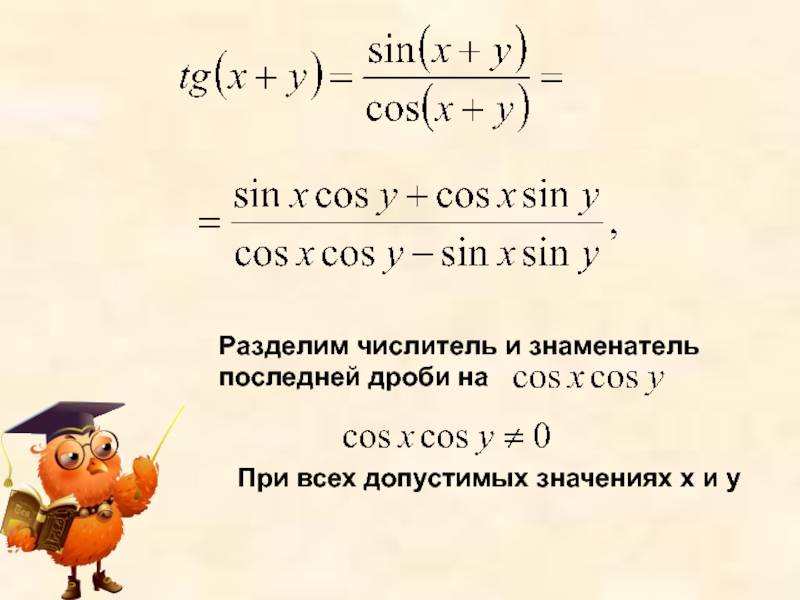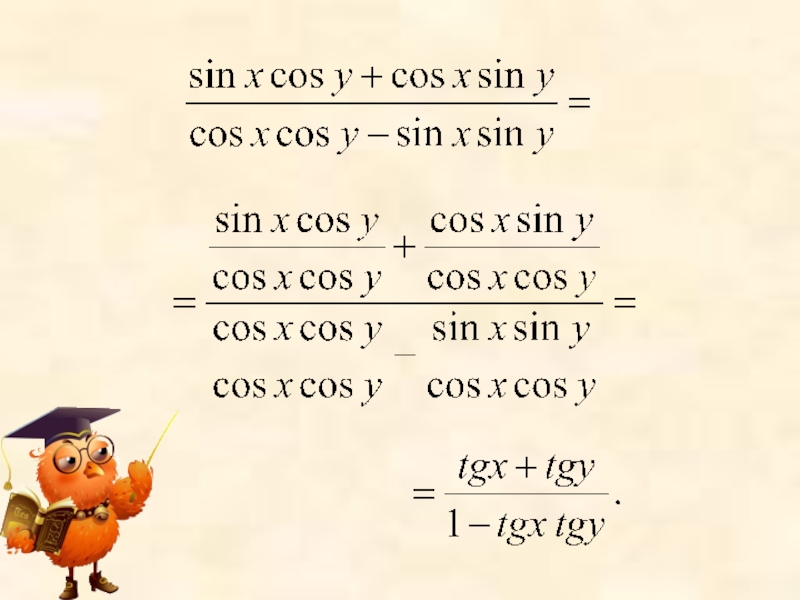Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тангенс суммы и разности аргументов 10 класс УМК А.Г. Мордкович
Содержание
- 1. Тангенс суммы и разности аргументов 10 класс УМК А.Г. Мордкович
- 2. ЦелиИзучить формулы тангенса суммы и разности аргументов.Рассмотреть практическое применение данных формул.
- 3. ПовторимСинус суммы двух аргументов равен произведению синуса
- 4. ПовторимКосинус суммы двух аргументов равен произведению косинусов этих аргументов минус произведение синусов этих аргументов.
- 5. ПовторимСинус разности двух аргументов равен произведению синуса
- 6. ПовторимКосинус разности двух аргументов равен произведению косинусов этих аргументов плюс произведение синусов этих аргументов.
- 7. Выведем формулу тангенса суммы двух аргументовПо определению
- 8. Разделим числитель и знаменатель последней дроби наПри всех допустимых значениях х и у
- 9. Слайд 9
- 10. Получили:Аналогично можно доказать, что
- 11. Пример 1.Вычислить:Решение.
- 12. Пример 2.Вычислить:Решение.
- 13. Пример 3.Вычислить:Решение.
- 14. Историческая страничка
- 15. Замена хорд синусами стала главным достижением средневековой
- 16. Тригонометрия необходима для астрономических расчётов, которые оформляются
- 17. Южноиндийские математики в XVI веке добились больших
- 18. Так, ряды для синуса и косинуса вывел Исаак
- 19. Джеймс ГрегориДата рождения: 1638Место рождения: Драмоук, ШотландияГотфрид Вильгельм ЛейбницДата
- 20. С VIII века учёные стран Ближнего и
- 21. После того как трактаты мусульманских ученых были
- 22. Решите из учебника№ 20.1, 20.3, 20.5, 20.7
- 23. Задание на дом§ 20 выучить№ 20.2, 20.4, 20.6
- 24. Список используемых источниковАлгебра и начала математического анализа.
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тангенс суммы и разности аргументов урок алгебры, 10 класс, УМК А.Г.
Мордкович
Енский Ковдорского района Мурманской областиСлайд 2Цели
Изучить формулы тангенса суммы и разности аргументов.
Рассмотреть практическое применение данных
формул.
Слайд 3Повторим
Синус суммы двух аргументов равен произведению синуса первого аргумента на
косинус второго плюс произведение косинуса первого аргумента на синус второго.
Слайд 4Повторим
Косинус суммы двух аргументов равен произведению косинусов этих аргументов минус
произведение синусов этих аргументов.
Слайд 5Повторим
Синус разности двух аргументов равен произведению синуса первого аргумента на
косинус второго минус произведение косинуса первого аргумента на синус второго.
Слайд 6Повторим
Косинус разности двух аргументов равен произведению косинусов этих аргументов плюс
произведение синусов этих аргументов.
Слайд 7Выведем формулу тангенса суммы двух аргументов
По определению тангенс есть отношение
синуса к косинусу одного и того же аргумента
По изученным формулам
синуса и косинуса суммы, получимСлайд 15Замена хорд синусами стала главным достижением средневековой Индии. Такая замена
позволила вводить различные функции, связанные со сторонами и углами прямоугольного
треугольника. В Индии было положено начало тригонометрии как учению о тригонометрических величинах.Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как
Средневековая Индия
Слайд 16
Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц.
Первая таблица синусов имеется в «Сурья-сиддхантеТригонометрия необходима для астрономических расчётов,
которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у АриабхатыТригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.Статуя Ариабхаты. Индийский межуниверситетский центр астрономии и астрофизики (IUCAA)
Слайд 17Южноиндийские математики в XVI веке добились больших успехов в области
суммирования бесконечных числовых рядов. В анонимном трактате «Каранападдхати» («Техника вычислений»)
даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв.Слайд 18Так, ряды для синуса и косинуса вывел Исаак НьютонТак, ряды для
синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был
найден Дж. ГрегориТак, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.Исаак Ньютон
Слайд 19Джеймс Грегори
Дата рождения: 1638
Место рождения:
Драмоук, Шотландия
Готфрид Вильгельм Лейбниц
Дата рождения:
21 июня (1
июля) 1646
Место рождения: Лейпциг, Саксония, Германия, Священная Римская империя
Слайд 20С VIII века учёные стран Ближнего и Среднего Востока развили
тригонометрию своих предшественников. В середине IX века среднеазиатский учёный аль-ХорезмиС VIII
века учёные стран Ближнего и Среднего Востока развили тригонометрию своих предшественников. В середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте».Аль-Хорезми
Имя при рождении: Мухаммад ибн Муса аль-Хорезми аль-Маджуси
Дата рождения:
не позднее 799 или 780
Слайд 21После того как трактаты мусульманских ученых были переведены на латынь,
многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской,
а затем и мировой науки.Слайд 24Список используемых источников
Алгебра и начала математического анализа. 10 – 11
классы. В 2ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений
(базовый уровень)/А.Г.Мордкович. – 11-е изд., стер. – М.: Мнемозина, 2010. – 399 с. : ил.http://gruzdoff.ru/wiki/http://gruzdoff.ru/wiki/Тригонометрия
http://gruzdoff.ru/wiki/http://gruzdoff.ru/wiki/Тригонометрия#.http://gruzdoff.ru/wiki/Тригонометрия#.D0.A1.D1.80.D0.B5.D0.B4.D0.BD.D0.B5.D0.B2.D0.B5.D0.BA.D0.BE.D0.B2.D0.B0.D1.8F_.D0.98.D0.BD.D0.B4.D0.B8.D1.8F