Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение прототипов В 8
Содержание
- 1. Решение прототипов В 8
- 2. Задание B8 (№ 40131)На рисунке изображен график
- 3. Задание B8 (№ 119971)На рисунке изображен график
- 4. Задание B8 (№ 27485)Прямая
- 5. Задание B8 (№ 27487)На рисунке изображен график
- 6. Задание B8 (№ 27488)На рисунке изображен график
- 7. Задание B8 (№ 27489)На рисунке изображен график
- 8. Задание B8 (№ 27490)На рисунке изображен график
- 9. Задание B8 (№ 27491)На рисунке изображен график
- 10. Задание B8 (№ 27492)На рисунке изображен график
- 11. Задание B8 (№ 27494)На рисунке изображен график
- 12. Задание B8 (№ 27496)На рисунке изображен график
- 13. Задание B8 (№ 27497)На рисунке изображен график
- 14. Задание B8 (№ 27500)На рисунке изображен график
- 15. Задание B8 (№ 27501)На рисунке изображен график
- 16. Задание B8 (№ 27503)На рисунке изображён график
- 17. Задание B8 (№ 119975)Материальная точка движется прямолинейно
- 18. Задание B8 (№ 119978)Материальная точка движется прямолинейно
- 19. Задание B8 (№ 119972)Прямая
- 20. Задание B8 (№ 119974)Прямая y=3x+4 является касательной
- 21. Задание B8 (№ 119973)Прямая y= - 5x+8
- 22. Так как по условию >0, то b= - 33. Ответ: - 33
- 23. Задание B8 (№ 27504)На рисунке изображён график
- 24. Задание B8 (№ 40129)На рисунке изображен график
- 25. Слайд 25
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
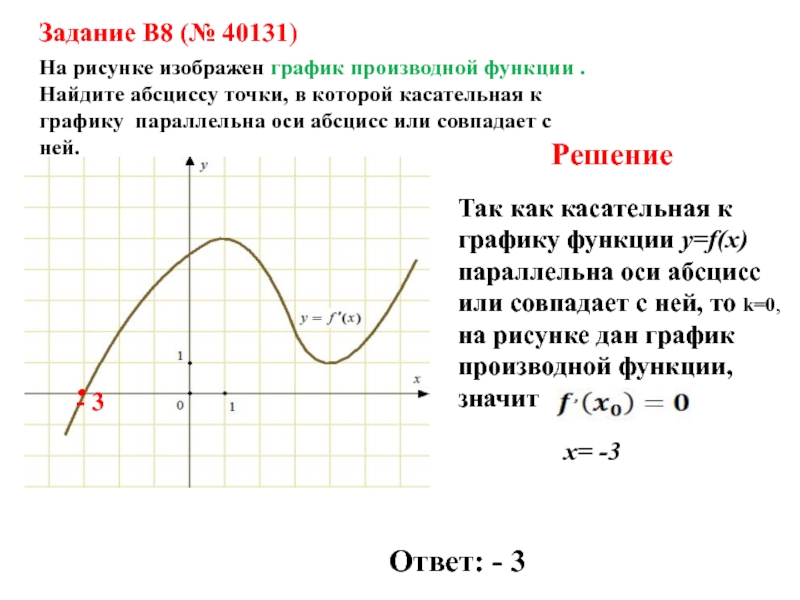
Задание B8 (№ 40131)
На рисунке изображен график производной функции .
Найдите абсциссу точки, в которой касательная к графику параллельна оси
абсцисс или совпадает с ней.Решение
Так как касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней, то k=0, на рисунке дан график производной функции, значит
x= -3
Ответ: - 3
.
- 3
Слайд 3
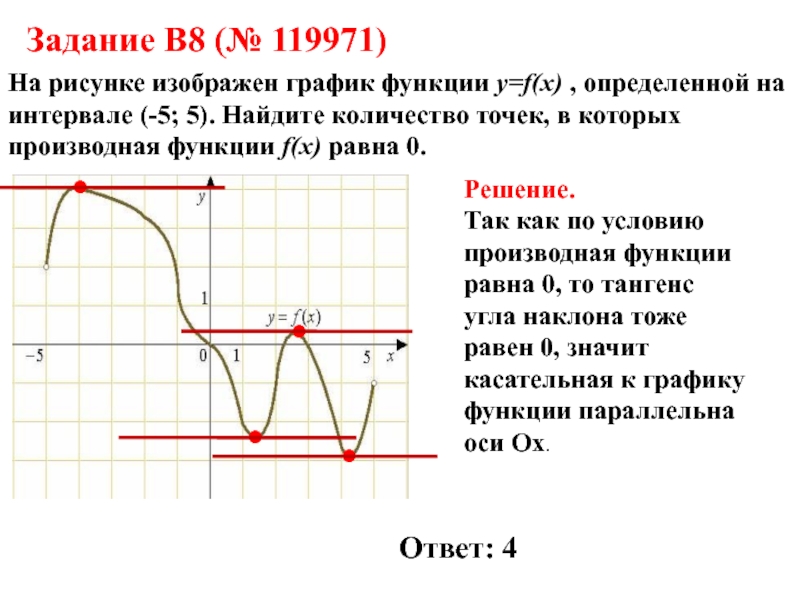
Задание B8 (№ 119971)
На рисунке изображен график функции y=f(x) ,
определенной на интервале (-5; 5). Найдите количество точек, в которых
производная функции f(x) равна 0.Решение.
Так как по условию производная функции равна 0, то тангенс угла наклона тоже равен 0, значит касательная к графику функции параллельна оси Ох.
.
.
.
.
Ответ: 4
Слайд 4
Задание B8 (№ 27485)
Прямая
параллельна касательной к графику функции
. Найдите абсциссу точки касания.Решение.
1).Так как прямая параллельна касательной, то их угловые коэффициенты равны, то есть k=7.
2). По геометрическому смыслу производной
где - абсцисса точки касания.
3). Ищем производную функции:
4). Решаем уравнение: 2 +6=7, =0,5.
Ответ: 0,5
Слайд 5
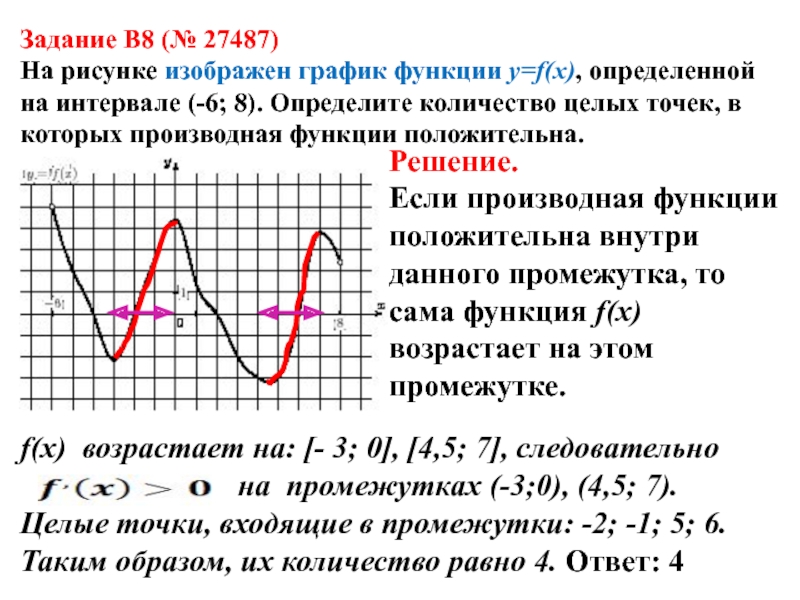
Задание B8 (№ 27487)
На рисунке изображен график функции y=f(x), определенной
на интервале (-6; 8). Определите количество целых точек, в которых
производная функции положительна.Решение.
Если производная функции положительна внутри данного промежутка, то сама функция f(x) возрастает на этом промежутке.
f(x) возрастает на: [- 3; 0], [4,5; 7], следовательно
на промежутках (-3;0), (4,5; 7).
Целые точки, входящие в промежутки: -2; -1; 5; 6.
Таким образом, их количество равно 4. Ответ: 4
Слайд 6
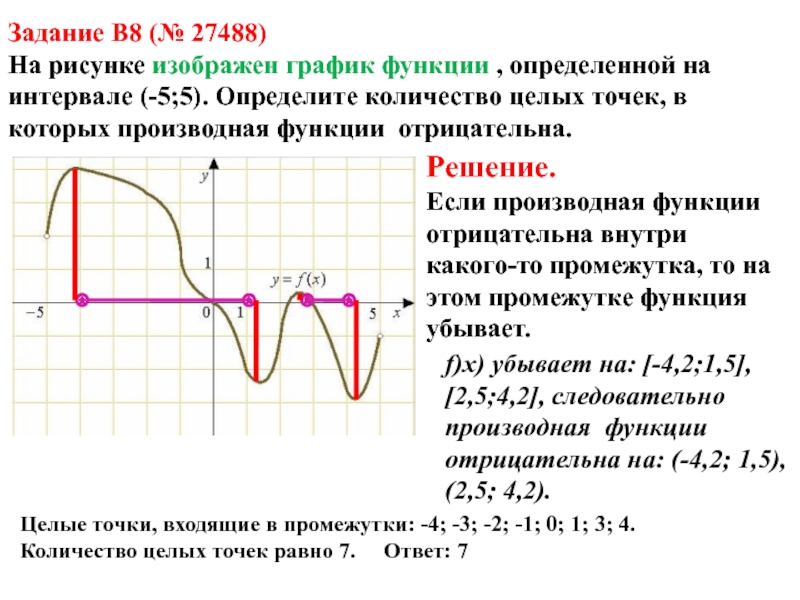
Задание B8 (№ 27488)
На рисунке изображен график функции , определенной
на интервале (-5;5). Определите количество целых точек, в которых производная
функции отрицательна.Решение.
Если производная функции отрицательна внутри какого-то промежутка, то на этом промежутке функция убывает.
f)x) убывает на: [-4,2;1,5],
[2,5;4,2], следовательно
производная функции отрицательна на: (-4,2; 1,5),
(2,5; 4,2).
Целые точки, входящие в промежутки: -4; -3; -2; -1; 0; 1; 3; 4.
Количество целых точек равно 7. Ответ: 7
Слайд 7
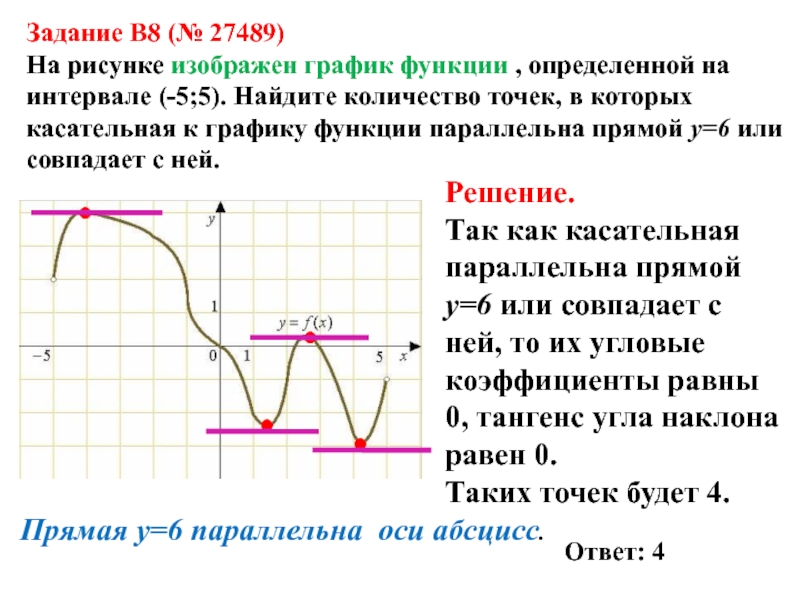
Задание B8 (№ 27489)
На рисунке изображен график функции , определенной
на интервале (-5;5). Найдите количество точек, в которых касательная к
графику функции параллельна прямой y=6 или совпадает с ней.Решение.
Так как касательная параллельна прямой y=6 или совпадает с ней, то их угловые коэффициенты равны 0, тангенс угла наклона равен 0.
Таких точек будет 4.
Ответ: 4
.
.
.
.
Прямая y=6 параллельна оси абсцисс.
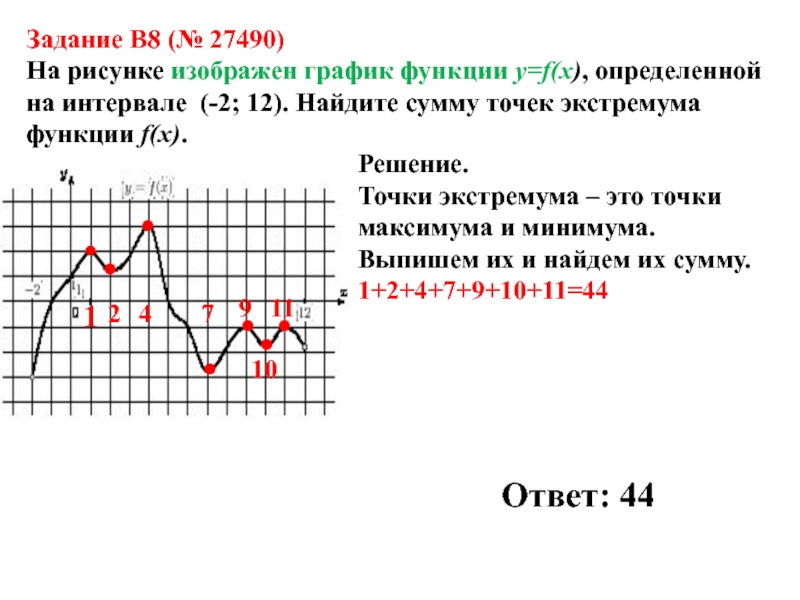
Слайд 8Задание B8 (№ 27490)
На рисунке изображен график функции y=f(x), определенной
на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).
Решение.
Точки
экстремума – это точки максимума и минимума.Выпишем их и найдем их сумму.
1+2+4+7+9+10+11=44
.
.
.
.
.
.
1
2
.
4
7
9
10
11
Ответ: 44
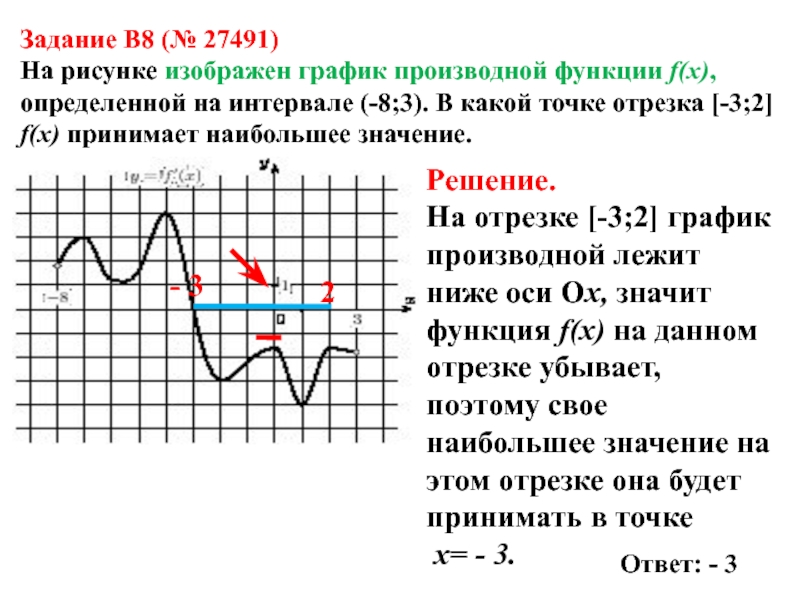
Слайд 9Задание B8 (№ 27491)
На рисунке изображен график производной функции f(x),
определенной на интервале (-8;3). В какой точке отрезка [-3;2] f(x)
принимает наибольшее значение.Решение.
На отрезке [-3;2] график производной лежит ниже оси Ох, значит функция f(x) на данном отрезке убывает, поэтому свое наибольшее значение на этом отрезке она будет принимать в точке
x= - 3.
Ответ: - 3
- 3
2
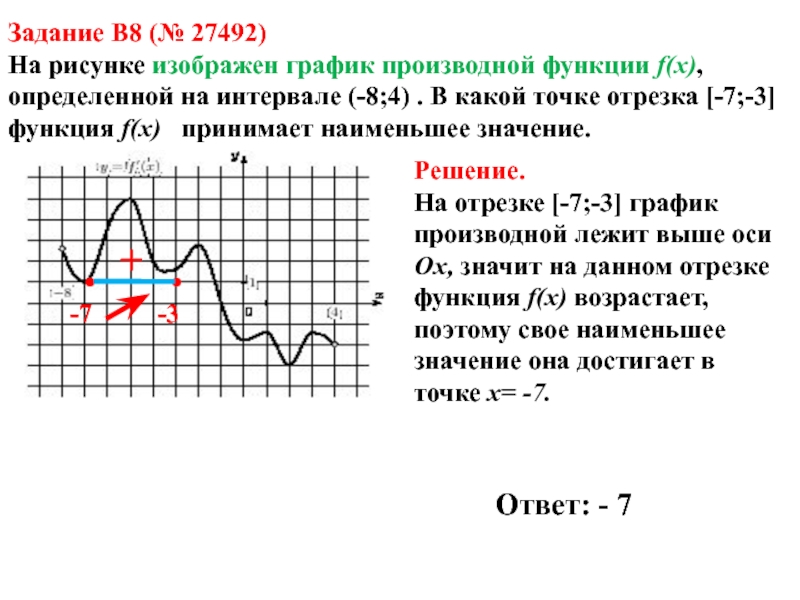
Слайд 10Задание B8 (№ 27492)
На рисунке изображен график производной функции f(x),
определенной на интервале (-8;4) . В какой точке отрезка [-7;-3]
функция f(x) принимает наименьшее значение.Решение.
На отрезке [-7;-3] график производной лежит выше оси Ох, значит на данном отрезке функция f(x) возрастает, поэтому свое наименьшее значение она достигает в точке x= -7.
-7
-3
+
.
.
Ответ: - 7
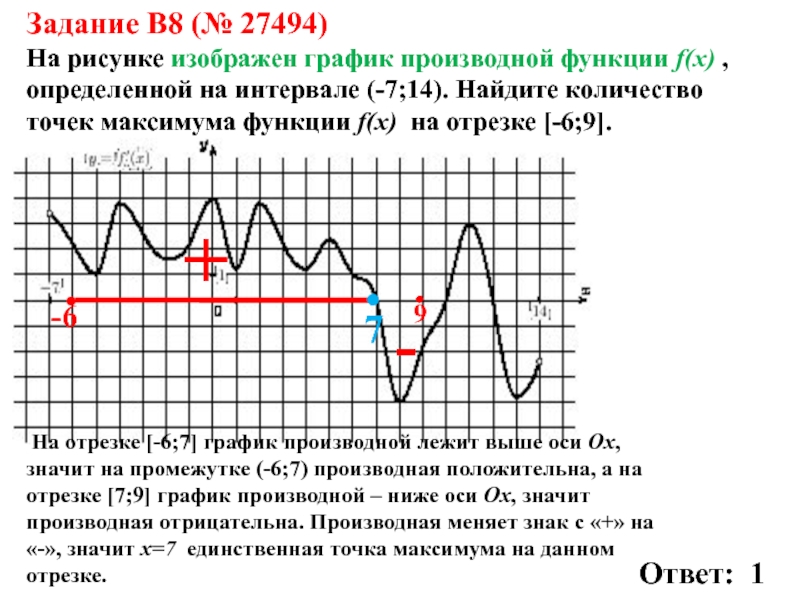
Слайд 11Задание B8 (№ 27494)
На рисунке изображен график производной функции f(x)
, определенной на интервале (-7;14). Найдите количество точек максимума функции
f(x) на отрезке [-6;9].-6
.
9
.
.
+
7
-
На отрезке [-6;7] график производной лежит выше оси Ох, значит на промежутке (-6;7) производная положительна, а на отрезке [7;9] график производной – ниже оси Ох, значит производная отрицательна. Производная меняет знак с «+» на «-», значит х=7 единственная точка максимума на данном отрезке.
Ответ: 1
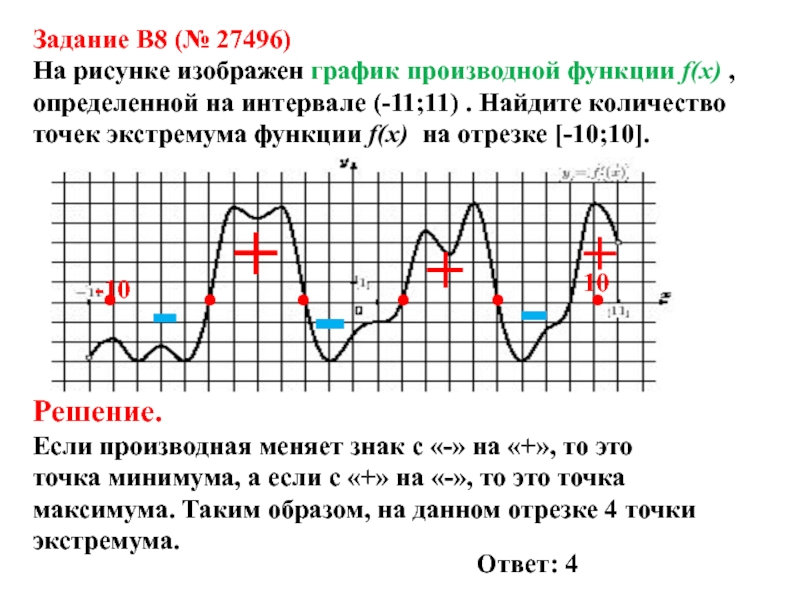
Слайд 12Задание B8 (№ 27496)
На рисунке изображен график производной функции f(x)
, определенной на интервале (-11;11) . Найдите количество точек экстремума
функции f(x) на отрезке [-10;10].-10
10
.
.
.
.
.
.
-
-
-
+
+
+
Решение.
Если производная меняет знак с «-» на «+», то это точка минимума, а если с «+» на «-», то это точка максимума. Таким образом, на данном отрезке 4 точки экстремума.
Ответ: 4
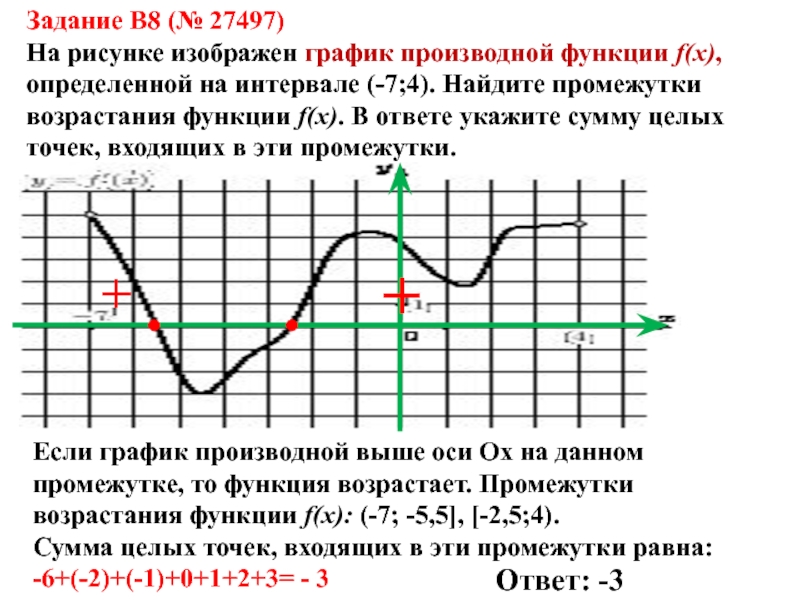
Слайд 13Задание B8 (№ 27497)
На рисунке изображен график производной функции f(x),
определенной на интервале (-7;4). Найдите промежутки возрастания функции f(x). В
ответе укажите сумму целых точек, входящих в эти промежутки.+
+
.
.
Если график производной выше оси Ох на данном промежутке, то функция возрастает. Промежутки возрастания функции f(x): (-7; -5,5], [-2,5;4).
Сумма целых точек, входящих в эти промежутки равна:
-6+(-2)+(-1)+0+1+2+3= - 3
Ответ: -3
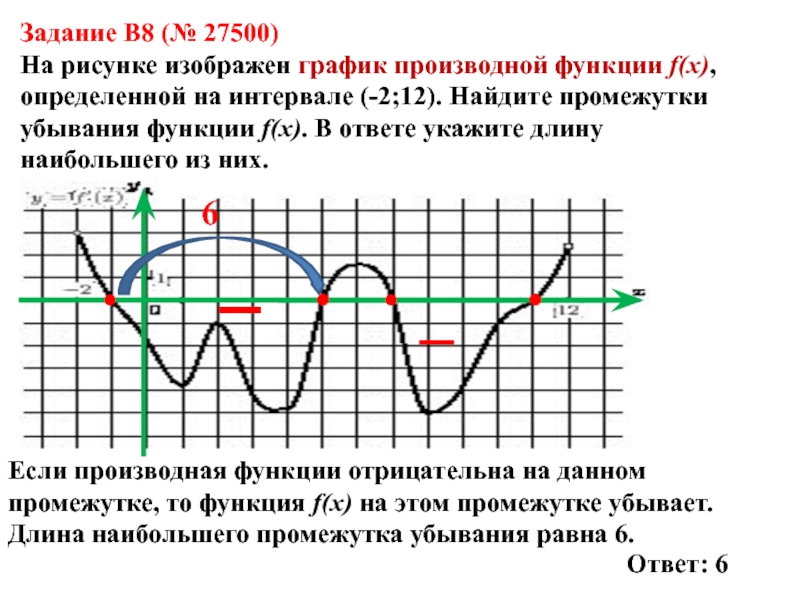
Слайд 14Задание B8 (№ 27500)
На рисунке изображен график производной функции f(x),
определенной на интервале (-2;12). Найдите промежутки убывания функции f(x). В
ответе укажите длину наибольшего из них..
.
.
_
_
Если производная функции отрицательна на данном промежутке, то функция f(x) на этом промежутке убывает.
Длина наибольшего промежутка убывания равна 6.
.
Ответ: 6
6
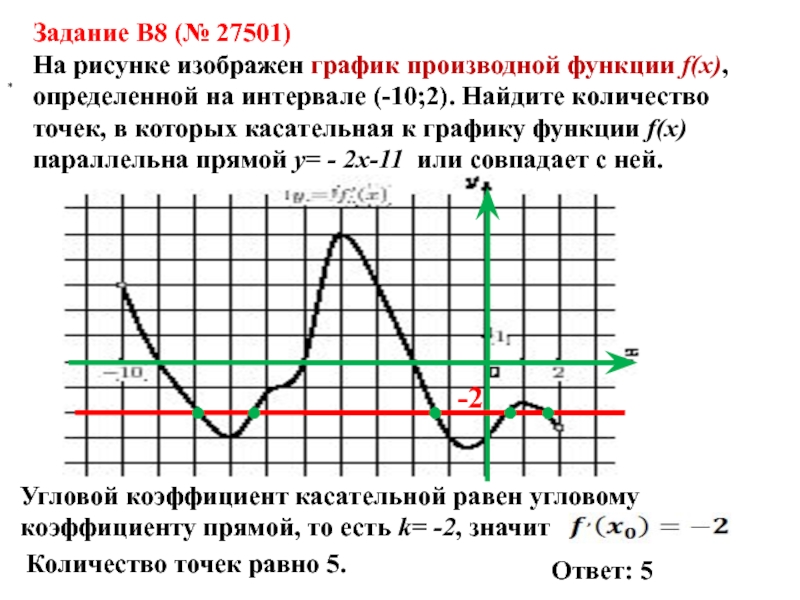
Слайд 15Задание B8 (№ 27501)
На рисунке изображен график производной функции f(x),
определенной на интервале (-10;2). Найдите количество точек, в которых касательная
к графику функции f(x) параллельна прямой y= - 2x-11 или совпадает с ней..
.
.
.
.
Угловой коэффициент касательной равен угловому коэффициенту прямой, то есть k= -2, значит
*
Количество точек равно 5.
Ответ: 5
-2
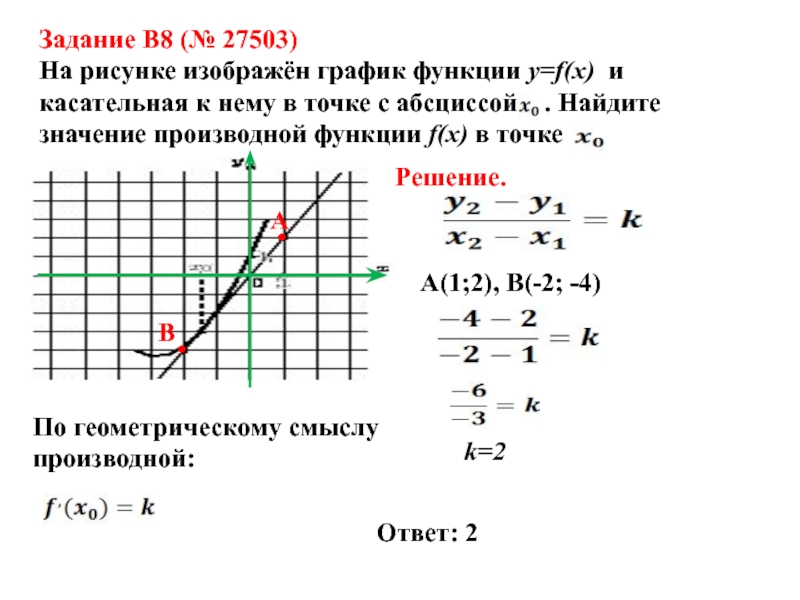
Слайд 16Задание B8 (№ 27503)
На рисунке изображён график функции y=f(x) и
касательная к нему в точке с абсциссой . Найдите
значение производной функции f(x) в точкеРешение.
А
.
.
В
А(1;2), В(-2; -4)
k=2
По геометрическому смыслу
производной:
Ответ: 2
Слайд 17Задание B8 (№ 119975)
Материальная точка движется прямолинейно по закону
(где x — расстояние от точки
отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t=9 с.Решение.
Так как t=9, то
Ответ: 60
Слайд 18Задание B8 (№ 119978)
Материальная точка движется прямолинейно по закону
(где x —
расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?Решение:
Ответ: 8
Слайд 19Задание B8 (№ 119972)
Прямая
является касательной к графику функции
. Найдите a.Решение:
Так как точка касания принадлежит графику функции, то ее координаты удовлетворяют уравнению:
Ответ: 0,125.
Слайд 20Задание B8 (№ 119974)
Прямая y=3x+4 является касательной к графику функции
Найдите c.
Решение:
Так как точка касания принадлежит графику функции, то ее координаты удовлетворяют уравнению:
Ответ: 7
Слайд 21Задание B8 (№ 119973)
Прямая y= - 5x+8 является касательной
к графику функции
. Найдите b, учитывая, что абсцисса точки касания больше 0.Решение:
Подставим координаты точки касания в функцию и найдем b.
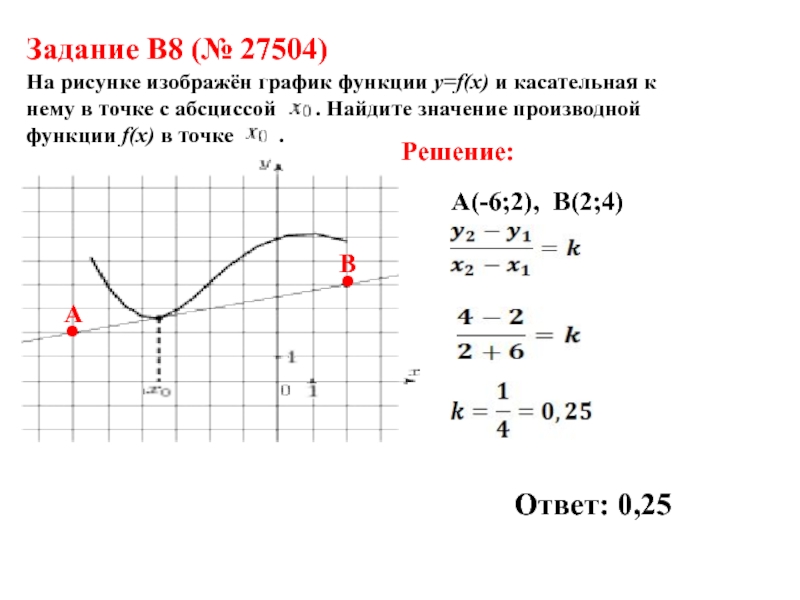
Слайд 23Задание B8 (№ 27504)
На рисунке изображён график функции и
касательная к нему в точке с абсциссой . Найдите
значение производной функции в точке .Задание B8 (№ 27504)
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
Решение:
А(-6;2), В(2;4)
Ответ: 0,25
.
.
А
В
Слайд 24Задание B8 (№ 40129)
На рисунке изображен график функции y=f(x). Прямая,
проходящая через начало координат, касается графика этой функции в точке
с абсциссой 8. Найдите .Решение.
Так как прямая проходит через начало координат и касается графика функции в точке с абсциссой 8, и учитывая, что
Найдем из прямоугольного треугольника .
8
10
Ответ: 1,25