Разделы презентаций

Бесконечно убывающая геометрическая прогрессия

Содержание

Рациональное число – это число, которое может быть записано в виде а/в, где ……..Всякое рациональное число может быть представлено в виде ……1) Закончите предложение:2 вариант1 вариант2)Как называются числа, представляемые бесконечными непериодическими

Слайды и текст этой презентации

Слайд 1АЛГЕБРА и начала анализа 10 класс Ш.А.Алимов, ю.м.колягин и др. 15

изд. М.: Просвещение, 2007
Учитель математики Пивоваренок Н.Н. ГОУ Школа №247
Глава I.

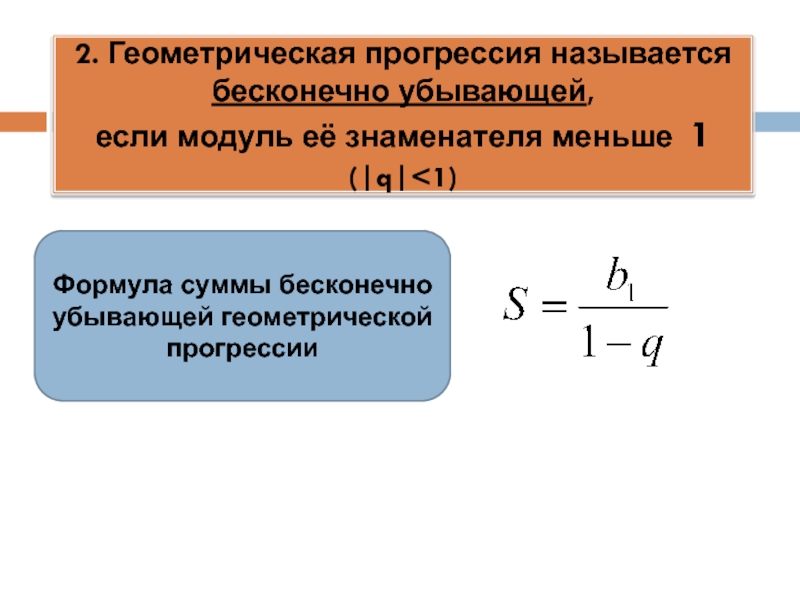
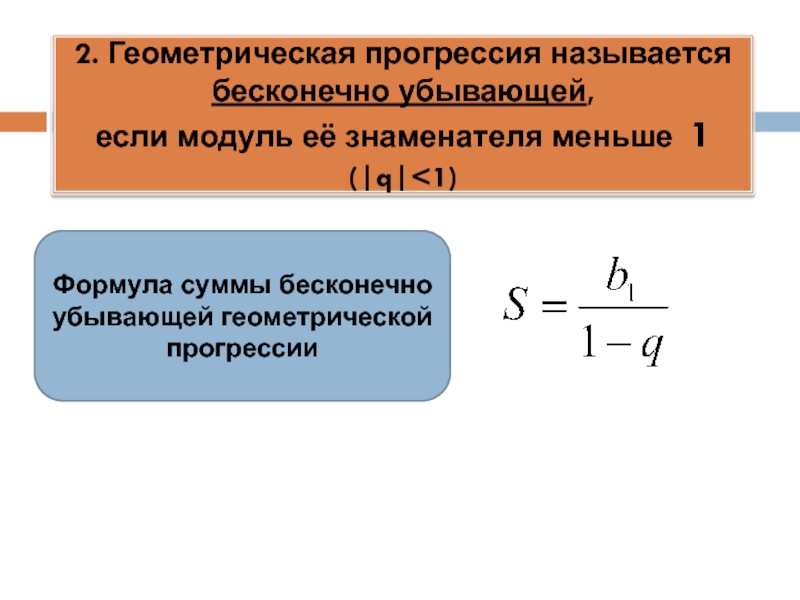
§3 Бесконечно убывающая геометрическая прогрессия Уроки 3-4

«Алгебра есть не что иное, как математический язык, приспособленный для обозначения отношений между количествами».
И. Ньютон

АЛГЕБРА и начала анализа 10 класс Ш.А.Алимов, ю.м.колягин и др. 15 изд. М.: Просвещение, 2007Учитель

Слайд 2Рациональное число – это число, которое может быть записано в

виде а/в, где ……..
Всякое рациональное число может быть представлено в

виде ……

1) Закончите предложение:

2 вариант

1 вариант

2)

Как называются числа, представляемые бесконечными непериодическими десятичными дробями?

Запиши какое-нибудь иррациональное число

3) Представьте число в виде периодической дроби:

4) Определите знак числа:

Рациональное число – это число, которое может быть записано в виде а/в, где ……..Всякое рациональное число может

Слайд 3 знать :
определение геометрической прогрессии;
определение бесконечно

убывающей геометрической прогрессии;
формулу суммы бесконечно убывающей геометрической прогрессии;

уметь применять формулу суммы бесконечно убывающей геометрической прогрессии ( в частности при записи бесконечной периодической десятичной дроби в виде обыкновенной)

§3 Бесконечно убывающая геометрическая прогрессия

Знания и навыки учащихся:

знать : определение геометрической прогрессии; определение бесконечно убывающей геометрической прогрессии; формулу суммы бесконечно

Слайд 41. Определение
Геометрическая прогрессия – такая числовая последовательность b1, b2,

b3, …, bn , …, что для всех натуральных n

выполняется равенство bn+1 = bnq , где bn≠0, q≠0
1. ОпределениеГеометрическая прогрессия – такая числовая последовательность b1, b2, b3, …, bn , …, что

Слайд 5Формула n-го члена геометрической последовательности:

Формула n-го члена геометрической последовательности:

Слайд 6Формула суммы первых n членов:

Формула суммы первых n членов:

Слайд 72. Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя

меньше 1 (|q|

2. Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше 1 (|q|

Слайд 82. Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя

меньше 1 (|q|

2. Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше 1 (|q|

Слайд 9№9(1,3,5), №10, №11, №12

№9(1,3,5), №10, №11, №12

Слайд 10№9(1,3,5)
№10, №11, №12

№9(1,3,5)№10, №11, №12

Слайд 11№10
№11, №12

№10№11, №12

Слайд 12§3, разобрать задачу 3 (стр.6);
№9 (2, 4, 6),
№11 (2),
№93 ,
№5

(2).
Домашнее задание

§3, разобрать задачу 3 (стр.6);№9 (2, 4, 6),№11 (2),№93 ,№5 (2).Домашнее задание

Слайд 13Итоги урока №3
Глава1 , §3
Самоанализ урока
10 класс

Итоги урока №3Глава1 , §3Самоанализ урока10 класс

Похожие презентации

"Стандартный вид числа". 310
Уравнения Уравнения 499
Построение графиков тригонометрических функций Построение графиков тригонометрических функций 301
Предел переменной величины Предел переменной величины 455
Тренажёр Тренажёр "Самоцветы для гнома" 2 класс 311
Одночлены и их особенности Одночлены и их особенности 553
Статистическое определение вероятности Статистическое определение вероятности 527
Тригонометрические функции Тригонометрические функции 447
Площадь криволинейной трапеции ИНТЕГРАЛ Площадь криволинейной трапеции ИНТЕГРАЛ 389
Решение задач по теории вероятностей Решение задач по теории вероятностей 440
Показательные уравнения и неравенства - урок в 11 классе Показательные уравнения и неравенства - урок в 11 классе 581
Свойства корней степени N Свойства корней степени N 455
Функция у = kx?, ее свойства и график Функция у = kx?, ее свойства и график 800
Возрастание и убывание функции 9 класс Возрастание и убывание функции 9 класс 515
Подготовка к ЕГЭ. Задачи В 10 Подготовка к ЕГЭ. Задачи В 10 385
Действия с рациональными числами 6 класс Действия с рациональными числами 6 класс 385
Геометрическая прогрессия Формула n-го члена Геометрическая прогрессия Формула n-го члена 509
Тест Тест "Вынесение общего множителя за скобки" 7 класс 380
Сравнительная степень прилагательных 4 класс Сравнительная степень прилагательных 4 класс 299
Корень n-й степени и его свойства Корень n-й степени и его свойства 544

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика