Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Возведение в квадрат суммы и разности двух выражений
Содержание
- 1. Возведение в квадрат суммы и разности двух выражений
- 2. Образовательные: -вывести формулы квадратов суммы и разности
- 3. Организационный момент. Актуализация опорных знаний (устная работа).Изучение
- 4. Знание только тогда знание, когда оно приобретено усилиямисвоей мысли, а не памятью. (Л.Н.Толстой)Эпиграф урока:
- 5. Слайд 5
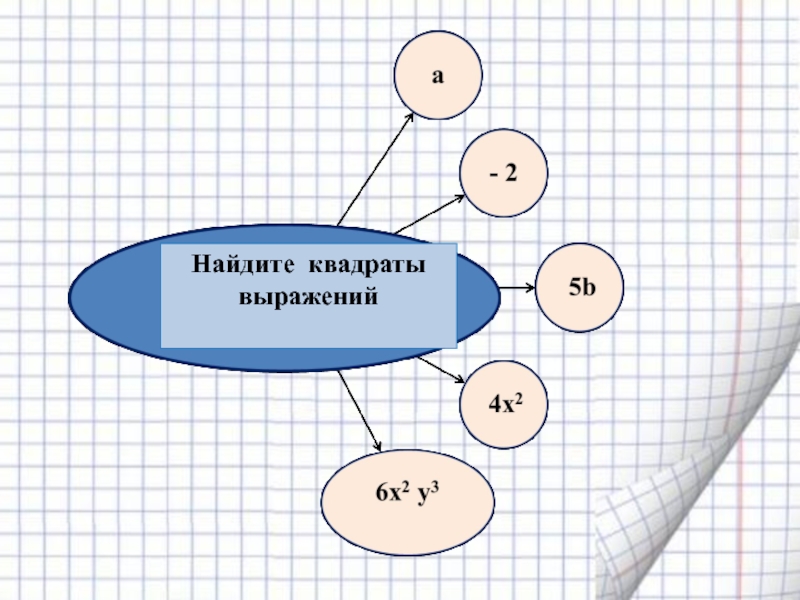
- 6. Найдите квадраты выражений
- 7. Слайд 7
- 8. Слайд 8
- 9. (x +2) · (y - 1) ( 3 – c) · (4 + b)Перемножьте многочлены
- 10. Слайд 10
- 11. 1 вариант(y + b) (y +b)
- 12. ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
- 13. ((6х + y) 2 = 36х2 +
- 14. Слайд 14
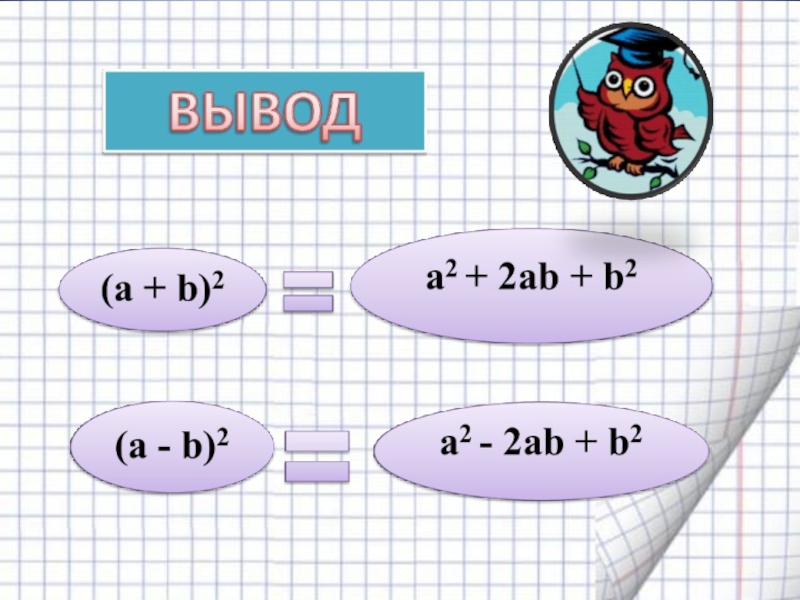
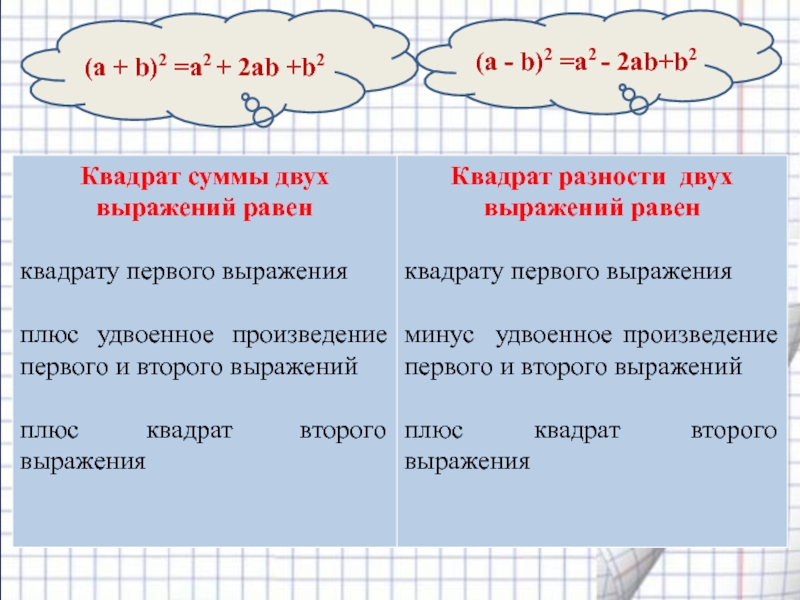
- 15. (а + b)2 =а2 + 2аb +b2(а - b)2 =а2 - 2аb+b2
- 16. ПРИМЕРЫ
- 17. Заполнить таблицу
- 18. , 4253х6
- 19. Геометрическая интерпретация формулы(a + b)2= a+ba+b
- 20. ФизминуткаВстали дружно, улыбнулись.Руки в стороны и
- 21. 1. № 862 (а, г, е, з)
- 22. ПРОВЕРКА= 302 + 2 · 30· 1
- 23. (а - b)2 = (b - а)2 (-а - b)2 =(а + b)2
- 24. 25²+250+5²=(25+5) ²=30²=90013²- 78+3² =(13-3)²=10²=100ПРОВЕРКА
- 25. Соедините пары тождественно равных выражений
- 26. Выбрать правильный ответ
- 27. 612 =(60+1) 2=602+2·60·1+12 = 3600+120+1=3721592=(60-1) 2=602-2·60·1+12=3600-120+1=3481
- 28. п. 31, доказать геометрический смысл формулы (a-b)2;№863(а, б, в, д); 866, №869(д, е). Домашнее задание.
- 29. -С какими формулами мы познакомились сегодня на
- 30. Скачать презентанцию
Образовательные: -вывести формулы квадратов суммы и разности двух чисел;-сформировать умение учащихся практически применять эти формулы для упрощения выражений, рационального вычисления числовых выражений.Развивающие : -развивать логическое мышление, внимание, память, сообразительность, культуру математической
Слайды и текст этой презентации
Слайд 2
Образовательные:
-вывести формулы квадратов суммы и разности двух чисел;
-сформировать умение
учащихся практически применять эти формулы для упрощения выражений, рационального вычисления
числовых выражений.Развивающие :
-развивать логическое мышление, внимание, память, сообразительность, культуру математической речи и культуру общения.
Воспитывающие:
-воспитывать ответственное отношение к деятельности, высокой познавательной активности и самостоятельности;
-воспитывать интерес к математике как учебному предмету через современные технологии преподавания;
- воспитывать чувство ответственности.
Цели урока:
Слайд 3
Организационный момент.
Актуализация опорных знаний (устная работа).
Изучение нового материала (исследовательская
работа)Изучение нового материала (исследовательская работа).
Первичное закрепление.
Геометрический смысл формул квадрата суммы.
Физминутка
(упражнения).Закрепление изученного материалаЗакрепление изученного материала.
Проверка усвоения изученного материала (первичный контроль знаний).
Домашнее задание.
Подведение итога урока.
План урока
Слайд 4
Знание только тогда знание,
когда оно приобретено усилиями
своей мысли, а
не памятью.
(Л.Н.Толстой)
Эпиграф урока:
Слайд 11 1 вариант
(y + b) (y +b)
(с + d
) (c +d)
(х + 2) (х+2)
2 вариант
(x – y) (x
– y)(m - n) (m- n)
(a – 2) (a – 2)
Слайд 20
Физминутка
Встали дружно, улыбнулись.
Руки в стороны и вверх.
Потянулись, оглянулись.
Вы
присели, теперь встали.
Руки в стороны и вверх.
Потянулись, улыбнулись.
Вы конечно, лучше
всех.
Слайд 21
1. № 862 (а, г, е, з)
2. Вычислить:
(30+1) 2 512 (30-1) 2 492
3. Преобразуйте выражения:
(а-7) 2 ( 5+х) 2
(7-а) 2 (-5-х) 2
Закрепление
изученного
материала.
Слайд 22ПРОВЕРКА
= 302 + 2 · 30· 1 + 12 =
900 + 60 + 1= 961
= 302 - 2
· 30· 1 + 12 = 900 – 60 +1= 841 = (50 + 1)2 = 502 + 2 · 50· 1 + 12 = 2500 + 100 + 1 = 2601
= (50 - 1)2 = 502 - 2 · 50· 1 + 12 = 2500 - 100 + 1 = 2401
Слайд 28
п. 31, доказать геометрический смысл формулы (a-b)2;
№863(а, б, в, д);
866, №869(д, е).
Домашнее задание.
Слайд 29-С какими формулами мы познакомились сегодня на уроке?
-Почему эти
формулы называются формулами сокращенного умножения?
-Чему равен квадрат суммы двух
выражений? -Чему равен квадрат разности двух выражений?
-Как вы думаете, зачем нужны нам эти формулы и стоит ли их запоминать?
Понравился ли вам урок?
Выставление отметок.
