Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МЕТОД ИНТЕРВАЛОВ ДЛЯ НЕПРЕРЫВНЫХ ФУНКЦИЙ
Содержание
- 1. МЕТОД ИНТЕРВАЛОВ ДЛЯ НЕПРЕРЫВНЫХ ФУНКЦИЙ
- 2. Просмотреть необходимо все, особо обратить внимание на
- 3. Основные задачи урокаобобщить ранее изученный материал о
- 4. Проверка домашнего задания1.Решить неравенство2. Решить неравенство:3.Решить неравенство: 4.Решить неравенство:5.Решить неравенство:
- 5. Определение 1: Если lim f(x) = f(x0)
- 6. Метод решения неравенств с одной переменной (Метод
- 7. Алгоритм решения неравенств методом интерваловНайти область определения
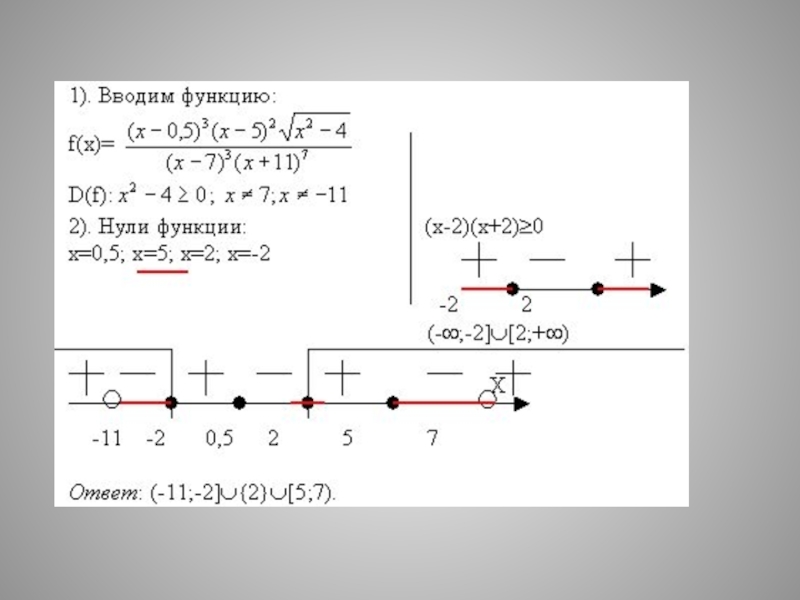
- 8. – Решим неравенство1) Найдем область определения неравенства:откуда3)
- 9. Решите неравенство1 вариант:2 вариант:Сделайте выводы о смене знака на интервалах, в зависимости от степени кратности корня.
- 10. выводы:
- 11. Решение уравнений и неравенств требует от учащихся
- 12. Слайд 12
- 13. 1.Решить неравенство:2.Решить неравенство
- 14. Слайд 14
- 15. Слайд 15
- 16. Домашнее заданиеЗаполнить всю таблицу, решив остальные неравенства.
- 17. Скачать презентанцию
Просмотреть необходимо все, особо обратить внимание на приведенные решения.Самим решить задания из 15 № 4,5,6.С остальным разберемся на элективных занятиях
Слайды и текст этой презентации
Слайд 2
Просмотреть необходимо все, особо обратить внимание на приведенные решения.
Самим решить
задания из 15 № 4,5,6.
Слайд 3Основные задачи урока
обобщить ранее изученный материал о решении неравенств методом
интервалов;
закрепить умения и навыки в решении рациональных неравенств;
Показать
возможность применения метода интервалов для решения неравенств различного типа;выработка умений и навыков в решении неравенств различного типа методом интервалов;
выработать навыки самооценки своей работы;
повысить интерес учащихся к нестандартным задачам, сформировать у них положительный мотив учения.
Слайд 4Проверка домашнего задания
1.Решить неравенство
2. Решить неравенство:
3.Решить неравенство:
4.Решить неравенство:
5.Решить неравенство:
Слайд 5Определение 1: Если lim f(x) = f(x0) при х х0,
то функцию f(x) называют непрерывной в точке х0.
Определение №2:
Если функция непрерывна в каждой точке некоторого промежутка I , то ее называют непрерывной на промежутке I (промежуток I называют промежутком непрерывности функции). График функции на этом промежутке представляет собой непрерывную линию, о которой говорят, что ее можно «нарисовать, не отрывая карандаша от бумаги».Слайд 6Метод решения неравенств с одной переменной (Метод интервалов) основан на
свойстве непрерывных функций.
Свойство:
Если на интервале (a; b) функция f(х) непрерывна
и не обращается в нуль, то она на этом интервале сохраняет постоянный знак. Пусть функция f (х)непрерывна на интервале I и обращается в нуль в конечном числе точек этого интервала. По сформулированному выше свойству непрерывных функций этими точками I разбивается на интервалы, в каждом из которых непрерывная функция f(х) сохраняет постоянный знак. Чтобы определить этот знак, достаточно вычислить значение функции f в какой-либо одной точке из каждого такого интервала.
Слайд 7Алгоритм решения неравенств методом интервалов
Найти область определения функции f(x);
Найти
нули функции f(x);
На числовую прямую нанести область определения и
нули функции. Нули функции разбивают ее область определения на промежутки, в каждом из которых функция непрерывна и сохраняет постоянный знак;Найти знаки функции в полученных промежутках, вычислив значение функции в какой-либо одной точке из каждого промежутка;
Записать ответ.
Слайд 8
–
Решим неравенство
1) Найдем область определения неравенства:
откуда
3) Находим корни многочлена
и определяем их кратность:
х =1 (четная кратность), корни 3,
-1, 0, 5, -2 (нечетная кратность). 4) Определим знак многочлена при х = 10, и расставим остальные знаки с учетом кратности корней.