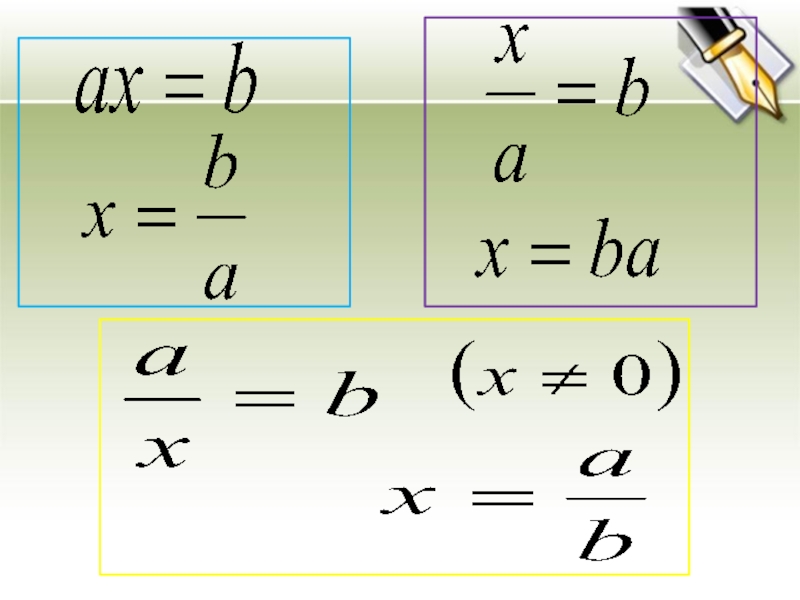Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Целое уравнение и его корни
Содержание
- 1. Целое уравнение и его корни
- 2. Целое уравнение и его корни1. Повторение. Схемы
- 3. Повторение: Линейные уравнения
- 4. Слайд 4
- 5. Решите уравнения:5 + х = 75 +
- 6. Поставь себе отметку!1 – 5 баллов6 – 9 баллов10 – 12 баллов13 баллов«2»«4»«5»«3»
- 7. Целое уравнение и его корниУравнения, в которых
- 8. Какова степень уравнения:А) Б)В)Г) 5652
- 9. Какова степень уравнения:Д) Е) 11
- 10. Что необходимо знать при решении уравнений?Формулы сокращённого умножения:Раскрытие скобок:
- 11. Что необходимо знать при решении уравнений?3. Раскрытие
- 12. Основные Методы решения целых уравнений1. Метод разложения
- 13. вынесения общего множителя за скобки способом группировкиПример.Разложить на множители можно с помощью
- 14. разложения квадратного трёхчлена на множители- корни квадратного трёхчленаРазложить на множители можно с помощью
- 15. 2. Метод введения новой переменнойСхема.Сделать
- 16. Пример.Введём замену:Тогда в новых переменных уравнение принимает вид:Вернёмся к замене:1)2) Ответ:
- 17. Биквадратное уравнение: Решение методом введения новой
- 18. 1. Алгебра. 9 класс: учеб.для общеобразова. учреждений/
- 19. Скачать презентанцию
Целое уравнение и его корни1. Повторение. Схемы решения простейших уравнений.2. Определение понятия целого уравнения.3. Справочный материал: Что необходимо знать при решении целых уравнений.4. Основные методы решения целых уравнений.
Слайды и текст этой презентации
Слайд 1МОУ «СОШ №12 ЗАТО Шиханы Саратовской области»
Шиханы, 2012
Целое уравнение
Учитель математики
МОУ «СОШ №12 ЗАТО Шиханы Саратовской области» Кондакова Татьяна Николаевна
Слайд 2Целое уравнение и его корни
1. Повторение. Схемы решения простейших
уравнений.
2.
Определение понятия целого уравнения.
3. Справочный материал: Что необходимо знать
при
решении целых уравнений.4. Основные методы решения целых уравнений.
Слайд 5Решите уравнения:
5 + х = 7
5 + х = 5
х
+ 3 = 7
5 + х = 2
х - 5
= 75 - х = 7
5 - х = 3
5 ∙ х = 7
х ∙ 5 = 5
х ∙ 5 = 1
5 ∙ х = 0
х = 2
х = -2
х = 2
х =
х = 1
х = 35
х =
х = 4
х = 12
х = -3
х = 0
х =
х = 0
Слайд 7Целое уравнение и его корни
Уравнения, в которых левая и правая
части
являются целыми выражениями, называются
целыми уравнениями.
многочлен стандартного вида
Степень уравнения
– это степень многочлена.Общая запись уравнения с одной переменной:
Решить уравнение – найти все корни многочлена Р(х) или установить, что их нет.
Слайд 11Что необходимо знать при решении
уравнений?
3. Раскрытие скобок:
4. Приведение
подобных слагаемых.
(Подобные слагаемые- слагаемые, имеющие
одинаковую буквенную часть)
Слайд 12Основные Методы решения
целых уравнений
1. Метод разложения на множители
Разложить на
множители можно с помощью
- применения формул сокращённого умножения
Слайд 13вынесения общего множителя
за скобки
способом группировки
Пример.
Разложить на множители можно
с помощью
Слайд 14разложения квадратного трёхчлена
на множители
- корни квадратного трёхчлена
Разложить на множители
можно с помощью
Слайд 152. Метод введения новой
переменной
Схема.
Сделать замену.
Решить уравнение в
новых
переменных.
3. Вернуться к замене.
4. Решить уравнения.
5. Ответ.
Слайд 16Пример.
Введём замену:
Тогда в новых переменных уравнение принимает вид:
Вернёмся к замене:
1)
2)
Ответ:
Слайд 17 Биквадратное уравнение:
Решение методом введения новой переменной:
Получим квадратное
уравнение:
-корни квадратного уравнения
Вернёмся к замене:
1)
2)
если
если
Ответ
Слайд 181. Алгебра. 9 класс: учеб.для общеобразова. учреждений/ Ю.Н. Макарычев, н,г,
Миндюк, к. И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского.17
–е изд. – М.: Просвещение, 2010. – 271с.Литература
2. 0M3158CAHR5URKCANWC03VCA2VOREACABKBYDECAEXFN5LCATHWDWCCAUS04I3CAE6397BCAZKKEWJCASJ88WVCAM07CL3CATY8OVKCATLGRIVCAEJUZQ3CAVRAEYKCA9F0EHUCAIH5CY7CAHBDH1YCA0URF07.jpg
