Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квадратичная функция, её свойства и график
Содержание
- 1. Квадратичная функция, её свойства и график
- 2. Цели урока:Повторить свойства квадратичной функции.Закрепить их знание
- 3. Учебно-воспитательные задачи:Образовательные: Приобретение знаний по применению графического
- 4. Оборудование: Геометрический инструмент.Компьютер Компьютерная презентация.Исторический материал.Метод: Словесный.Практический.Групповая
- 5. Ход урока1. Организационный момент.2. Вести с урока.1)
- 6. Определение.Функция вида у = ах2+bх+с,где
- 7. График квадратичной функции -Парабола Пара́бола (греч. παραβολή
- 8. Свойства Парабола — кривая второго порядка.Она имеет
- 9. ⮚Определить координаты вершины параболы.⮚ Уравнение оси симметрии
- 10. Вершина параболы:
- 11. Координаты точек пересечения параболы с осями координат.С
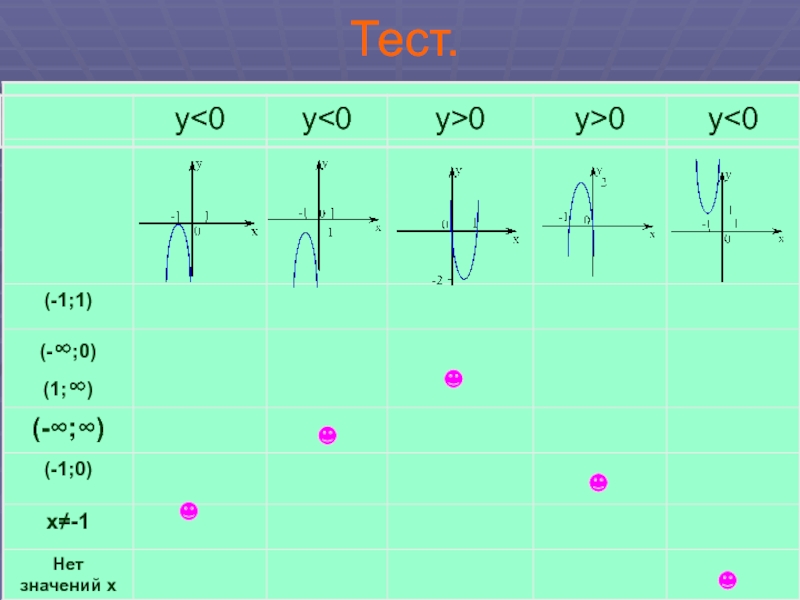
- 12. Тест
- 13. Построить график функции и по графику выяснить ее свойства.У = -х2-6х-8Свойства функции:у>0 на промежуткеу
- 14. Тест.
- 15. Скачать презентанцию
Цели урока:Повторить свойства квадратичной функции.Закрепить их знание при построении графиков квадратичной функции.Уметь определять свойства функции по графику.Показать связь квадратичной функции и её графика с реальным миром
Слайды и текст этой презентации
Слайд 2Цели урока:
Повторить свойства квадратичной функции.
Закрепить их знание при построении графиков
квадратичной функции.
и её графика с реальным миромСлайд 3Учебно-воспитательные задачи:
Образовательные:
Приобретение знаний по применению графического изображения квадратичной функции.
Применение
приемов решения задач.
Развивающие:
Совершенствование умения строить параболу.
Применение свойств квадратичной функции
в других и их взаимосвязь с математикой.Воспитательные:
Пробудить интерес к истории математики.
Способствовать расширению кругозора через информационный материал, диалоги и совместные размышления.
Слайд 4Оборудование:
Геометрический инструмент.
Компьютер
Компьютерная презентация.
Исторический материал.
Метод:
Словесный.
Практический.
Групповая работа.
Защита проектов.
Тип урока:
заключительный по теме:
“Квадратичная функция” с использованием активных методов.
Слайд 5Ход урока
1. Организационный момент.
2. Вести с урока.
1) повторить определение квадратичной
функции, ее свойства и график. (Фронтальная работа).
2) понятие параболы.
(Ученик объясняет, используя компьютерную презентацию)3) различие параболы: по направлению ветвей, по координатам вершин, по коэффициенту а,
4) Применение параболы в физике, технике, архитектуре, вокруг нас.
Слайд 6Определение.
Функция вида у = ах2+bх+с,
где а, b, c
– заданные числа, а≠0,
х – действительная переменная, называется квадратичной функцией.
Примеры:
1)
у=5х+1 4) у=x3+7x-12) у=3х2-1 5) у=4х2
3) у=-2х2+х+3 6) у=-3х2+2х
Слайд 7График квадратичной функции -Парабола
Пара́бола (греч. παραβολή — приложение) —
геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы)
и данной точки (называемой фокусом параболы).Слайд 8Свойства
Парабола — кривая второго порядка.
Она имеет ось симметрии, называемой осью
параболы. Ось проходит через фокус и перпендикулярна директрисе.
Если фокус параболы
отразить относительно касательной, то его образ будет лежать на директрисе.Парабола является антиподерой прямой.
Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
Слайд 9
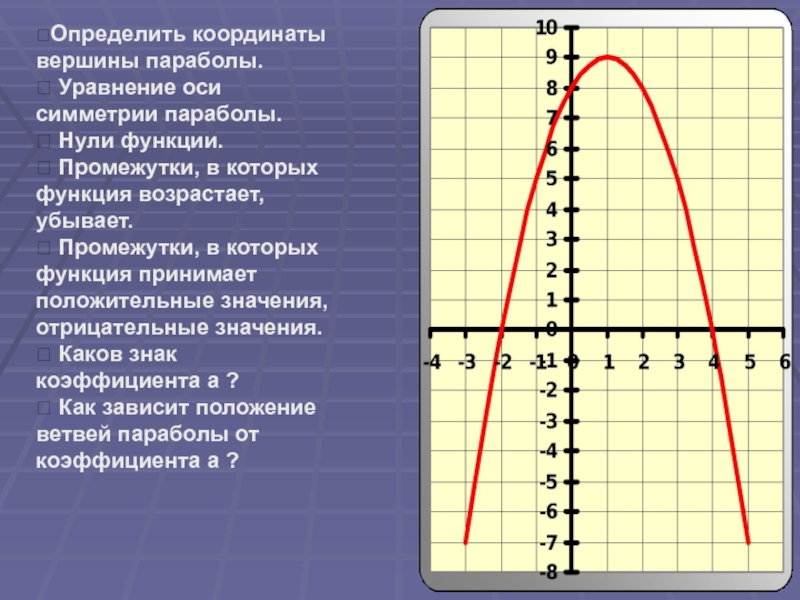
⮚Определить координаты вершины параболы.
⮚ Уравнение оси симметрии параболы.
⮚ Нули функции.
⮚
Промежутки, в которых функция возрастает, убывает.
⮚ Промежутки, в которых функция
принимает положительные значения, отрицательные значения.⮚ Каков знак коэффициента a ?
⮚ Как зависит положение ветвей параболы от коэффициента a ?
Слайд 10Вершина параболы:
Задание.
Найти
координаты вершины параболы:
1) у = х 2 -4х-5 2) у=-5х 2+3Ответ:(2;-9) Ответ:(0;3)
Уравнение оси симметрии: х=х0
Слайд 11Координаты точек пересечения параболы с осями координат.
С Ох: у=0
ах2+bх+с=0
С Оу: х=0
у=сЗадание.
Найти координаты точек пересечения параболы с осями координат:
1)у=х2-х; 2)у=х2+3; 3)у=5х2-3х-2
(0;0);(1;0) (0;3) (1;0);(-0,4;0);(0;2)
Слайд 13Построить график функции и по графику выяснить ее свойства.
У =
-х2-6х-8
Свойства функции:
у>0 на промежутке
у
на промежуткеНаибольшее значение функции равно
(-4;-2)
(-∞;-4);(-2;∞)
(-∞;-3]
[-3;∞)
1, при х=-3