Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества и операции над ними 9 класс
Содержание
- 1. Множества и операции над ними 9 класс
- 2. Задачи урока:Познакомиться с понятием множества и его
- 3. КАНТОР (Cantor) Георг (1845—1918) - немецкий
- 4. МНОЖЕСТВОМножество - одно из основных понятий современной
- 5. конечныебесконечныеВиды множеств
- 6. ЭЛЕМЕНТЫ МНОЖЕСТВАОбъекты, из которых образовано множество, называются
- 7. А = {1, 2, 3, 4, 5,
- 8. Два множества А и В называются равными ( А = В ), если
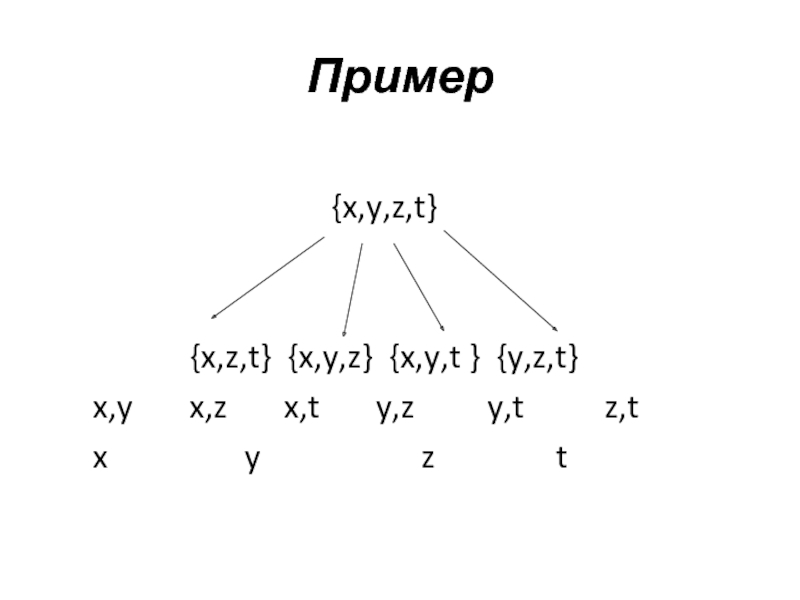
- 9. Пример{x,y,z,t}
- 10. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ Пересечением двух множеств А
- 11. Слайд 11
- 12. Разность множествА ВРазностью множеств А и В
- 13. ЗАДАНИЕ НА ДОМ§ 31, 1 уровень -
- 14. Понятие множества таит в себе опасность появления
- 15. Одному солдату было приказано брить тех и
- 16. Приведите примеры множества, элементами которого являются:а) животные;
- 17. Перечислите элементы множеств:а) частей света; б) деревьев; в) материков; г) цветов радуги.
- 18. Среди перечисленных ниже множеств укажите конечные и
- 19. Даны множества:А – множество фруктов в корзине;
- 20. БЛИЦ-ОПРОС
- 21. БЛИЦ-ОПРОСземноводные, млекопитающие, хладнокровные и т.п.Какие названия применяются для обозначения множеств животных?
- 22. БЛИЦ-ОПРОСрота, взвод, полк, дивизия и т.п.Какие названия применяются для обозначения множеств военно-служащих?
- 23. БЛИЦ-ОПРОСбукетКак называется множество цветов, стоящих в вазе?
- 24. БЛИЦ-ОПРОСфлотилия, эскадраКакие названия применяют для обозначения множеств кораблей?
- 25. БЛИЦ-ОПРОСдинастияКак называется множество царей (фараонов, императоров и т.д.) данной страны, принадлежащих одному семейству?
- 26. БЛИЦ-ОПРОСэкваторКак называется множество точек земной поверхности, равноудаленных от обоих полюсов?
- 27. БЛИЦ-ОПРОСдеревня, село, город, посёлокКак называется множество населённых людьми мест?
- 28. БЛИЦ-ОПРОСвыставка, галереяКак называется множество картин?
- 29. БЛИЦ-ОПРОСархивКак называется множество документов?
- 30. сегодня я узнал…было интересно…теперь я могу…меня удивило…я научился…мне захотелось…я приобрел…
- 31. БЛАГОДАРЮ ЗА УРОК
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Задачи урока:
Познакомиться с понятием множества и его элементами.
Виды множеств.
Способы задания
множеств.
Слайд 3КАНТОР (Cantor) Георг (1845—1918) -
немецкий математик, логик, теолог,
создатель теории бесконечных множеств, оказавшей определяющее влияние на развитие математических
наук на рубеже 19— 20 вв.Теория множеств появилась на свет 7 декабря 1873 года.
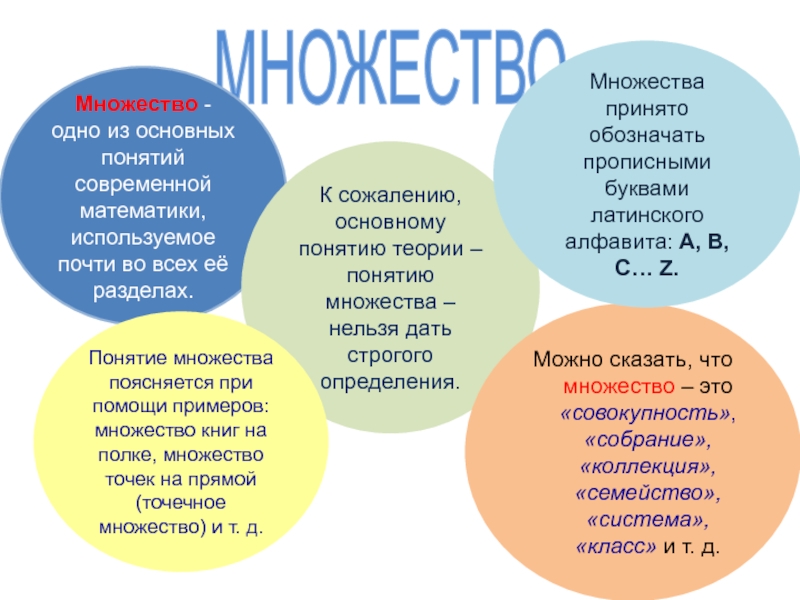
Слайд 4МНОЖЕСТВО
Множество - одно из основных понятий современной математики, используемое почти
во всех её разделах.
К сожалению, основному понятию теории – понятию
множества – нельзя дать строгого определения.Можно сказать, что множество – это «совокупность», «собрание», «коллекция», «семейство», «система», «класс» и т. д.
Понятие множества поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д.
Множества принято обозначать прописными буквами латинского алфавита: A, B, C… Z.
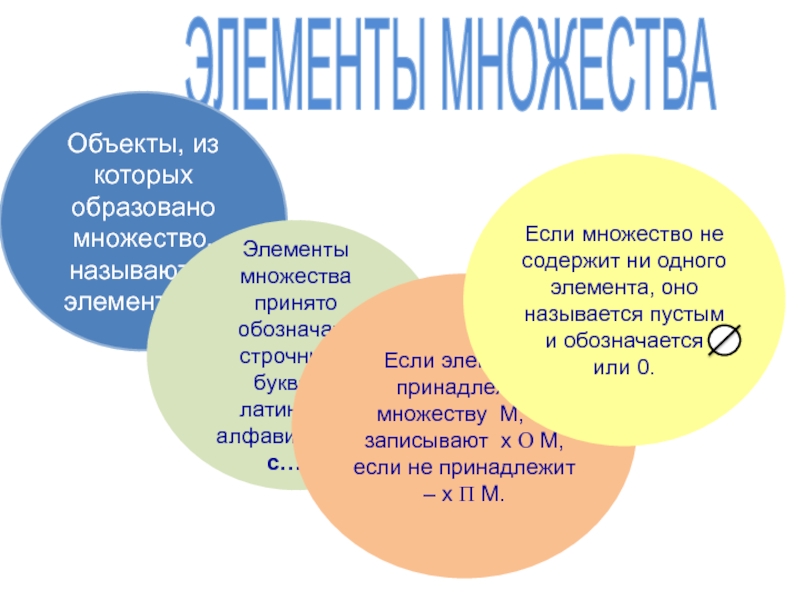
Слайд 6ЭЛЕМЕНТЫ МНОЖЕСТВА
Объекты, из которых образовано множество, называются элементами.
Элементы множества принято
обозначать строчными буквами латинского алфавита: a, b, c… z.
Если элемент
х принадлежит множеству М, то записывают х О М, если не принадлежит – x П M.Если множество не содержит ни одного элемента, оно называется пустым и обозначается
или 0.
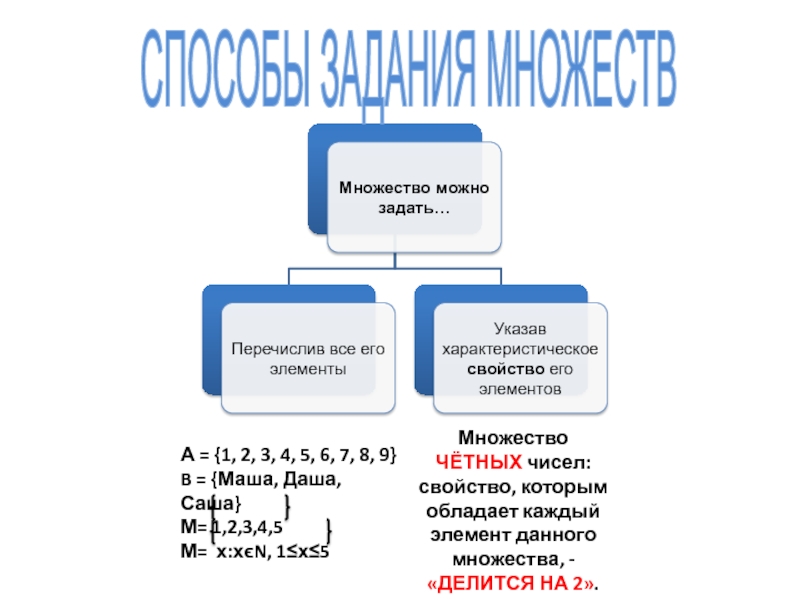
Слайд 7А = {1, 2, 3, 4, 5, 6, 7, 8,
9}
B = {Маша, Даша, Саша}
М= 1,2,3,4,5
М= х:хϵN, 1≤х≤5
Множество ЧЁТНЫХ чисел:
свойство, которым обладает каждый элемент данного множества, - «ДЕЛИТСЯ НА 2».СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ
Слайд 8Два множества А и В называются равными
( А = В ), если они состоят из
одних и тех же элементов, то есть каждый элемент множества А является
элементом множества В и наоборот, каждый элемент множества В является элементом множества А.Если каждый элемент множества А является
элементом множества В, то множество А называется подмножеством В.
Обозначение: А В.
Знак « » - знак включения.
Слайд 10ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
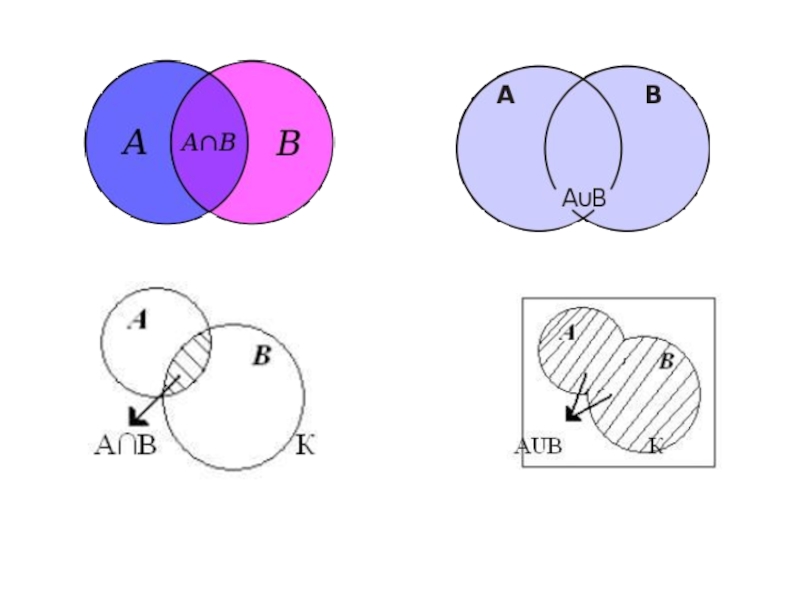
Пересечением
двух множеств А и В, называется
множество, которое состоит из всех элементов, лежащих одновременно в множестве
А и в множестве В.Объединением
двух множеств А и В называется множество, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств - или А или В.
АВ= {x xA и xB}
А В={x xA или xB}
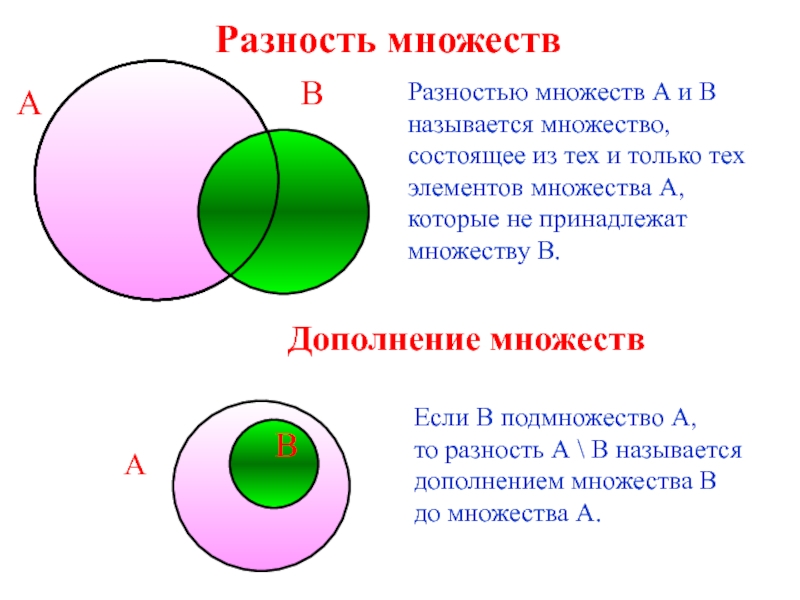
Слайд 12Разность множеств
А
В
Разностью множеств А и В
называется множество,
состоящее
из тех и только тех
элементов множества А,
которые не
принадлежат множеству В.
А
В
Если В подмножество А,
то разность А \ В называется
дополнением множества В
до множества А.
Дополнение множеств
Слайд 13ЗАДАНИЕ НА ДОМ
§ 31,
1 уровень - Параграф 31; №420(2;4),
№424(2;4), 429, тест.
2 уровень – Параграф 31, №429, выполнить тест.
Слайд 14Понятие множества таит в себе опасность появления противоречий или, как
ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко
не всякие конструкции и не всякие множества можно рассматривать.«Парадокс брадобрея»
Слайд 15Одному солдату было приказано брить тех и только тех солдат
его взвода, которые сами себя не бреют.
Неисполнение приказа в
армии, как известно, тягчайшее преступление. Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить.
Слайд 16Приведите примеры множества, элементами которого являются:
а) животные;
б) составные числа;
в) простые числа;
г) треугольники.
Слайд 18Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
а) множество
чисел, кратных 11; б) множество делителей числа 5; в) множество океанов; г) множество
натуральных чисел; д) множество рек Ростовской области; е) множество корней уравнения х - 3 = 10; ж) множество решений неравенства х + 2 < 3.Слайд 19Даны множества:
А – множество фруктов в корзине;
В – множество яблок
в этой корзине; С – множество груш в этой корзине; Д –
множество слив в этой корзине.Чем являются множества В, С и Д для множества А?