переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины
х сответсвует определенное значение другой величины у.Такое соответствие может быть задано различном образом , например : формулой, графически или таблицей.
С помощью функции математически выражаются многообразные количественные закономерности в природе.




![Обратные тригонометрические функции 10 класс у = arcsin x Функция y = sin x, рассматриваемая на у = arcsin x Функция y = sin x, рассматриваемая на промежутке [ -П/2 ; П/2] ,](/img/thumbs/cfc65701713930c29233f0e1c5b19aae-800x.jpg)
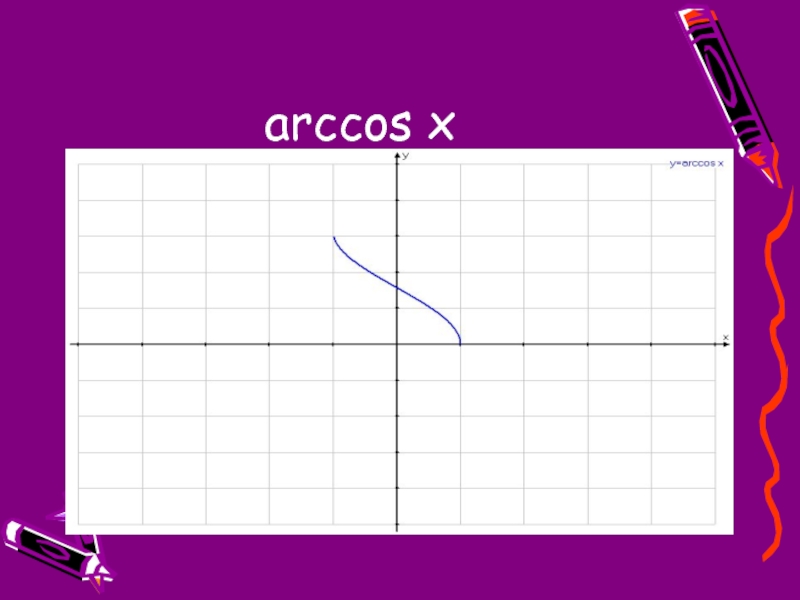
![Обратные тригонометрические функции 10 класс у = arccos xФункция у = cos x, рассматриваемая на промежутке у = arccos xФункция у = cos x, рассматриваемая на промежутке [0;П], имеет обратную функцию, которую называют](/img/tmb/4/382094/713e63d79f47559100341d3b88c931b8-800x.jpg)