Тригонометрические функции
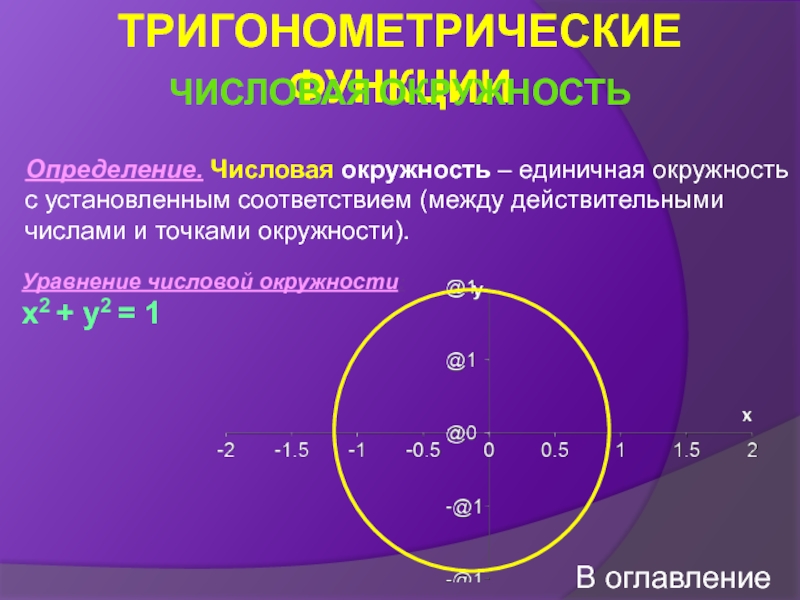
Числовая окружность
Синус и косинус
Тангенс и котангенс
Тригонометрические функции
числового аргументаФункция y = sin x
Свойства функции y = sin x
Функция y = cos x
Свойства функции y = cos x
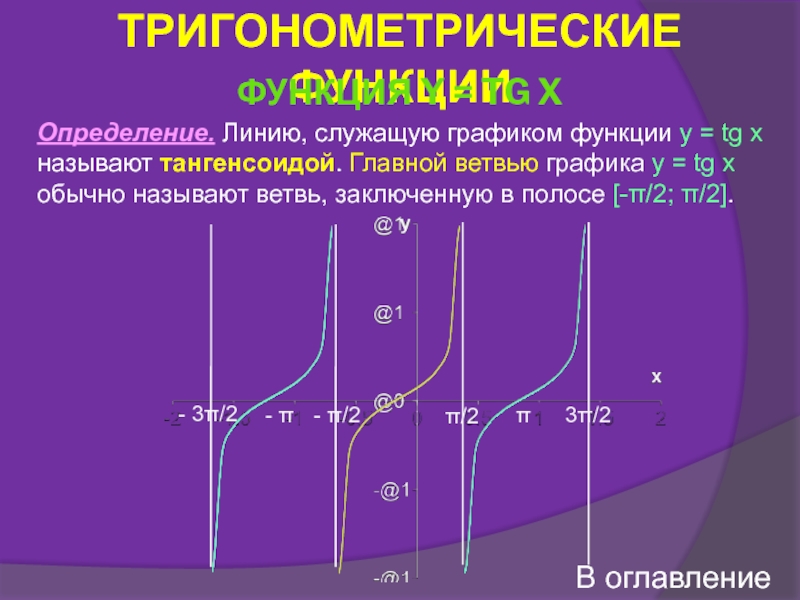
Функция y = tg x
Свойства функции y = tg x
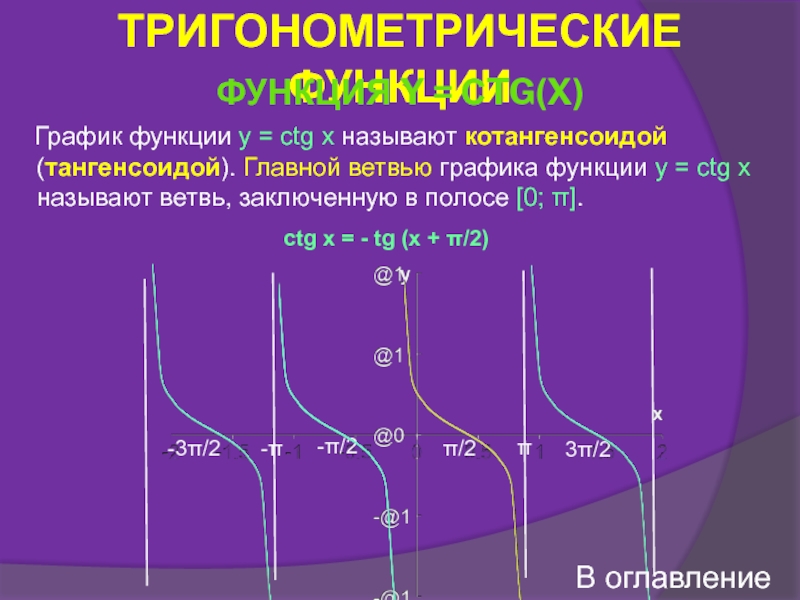
Функция y = ctg x
Свойства функции y = ctg x
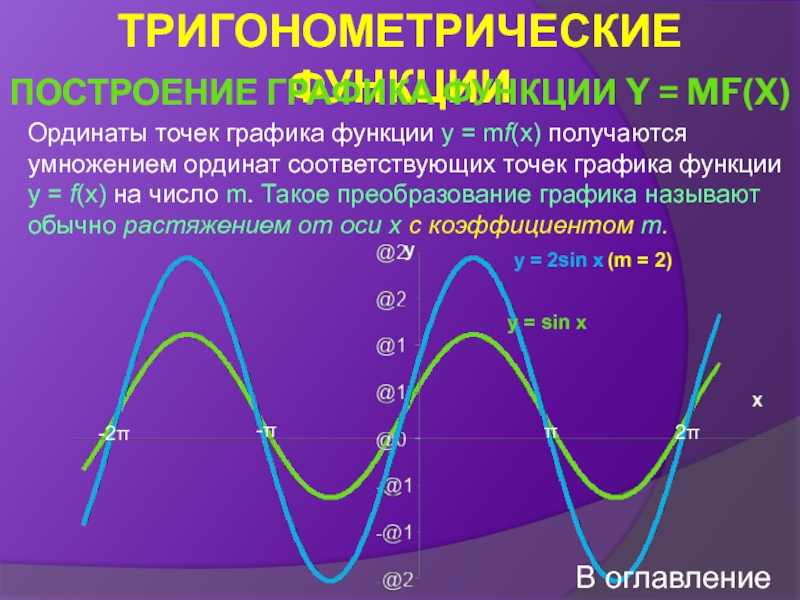
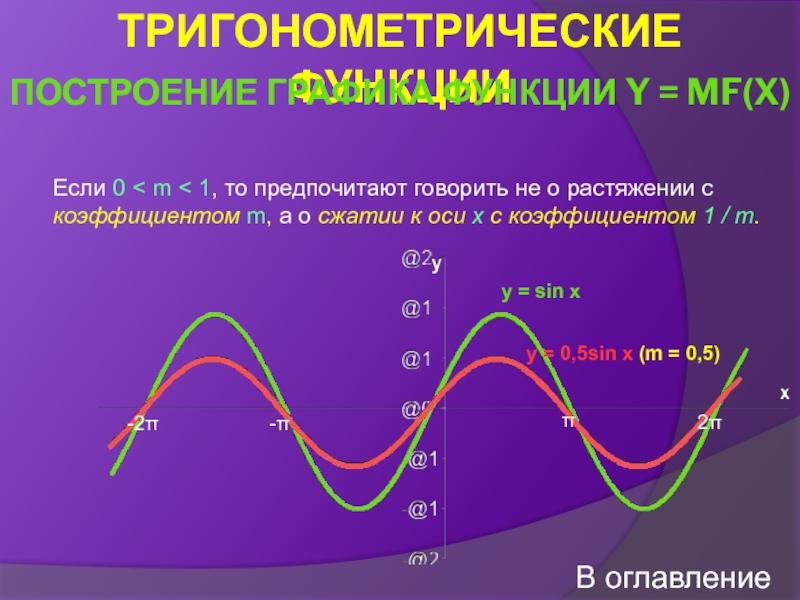
Построение графика функции y = mf(x)
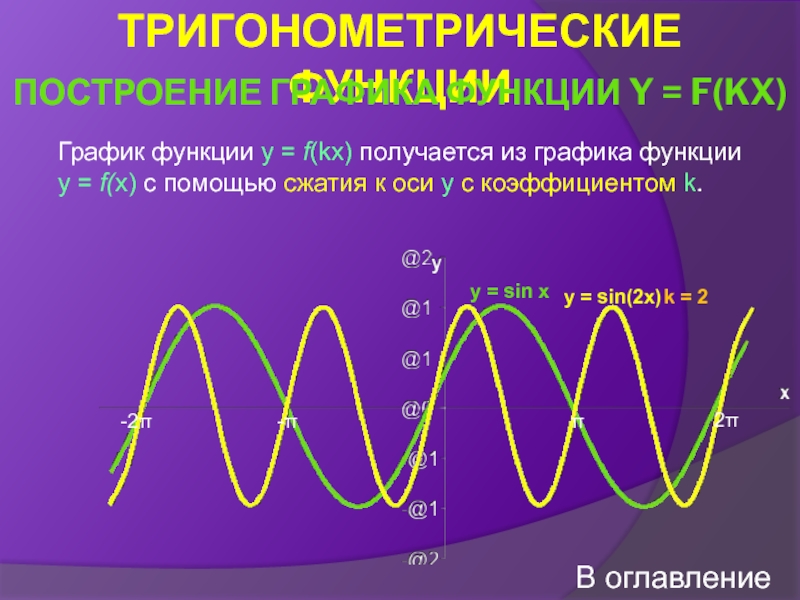
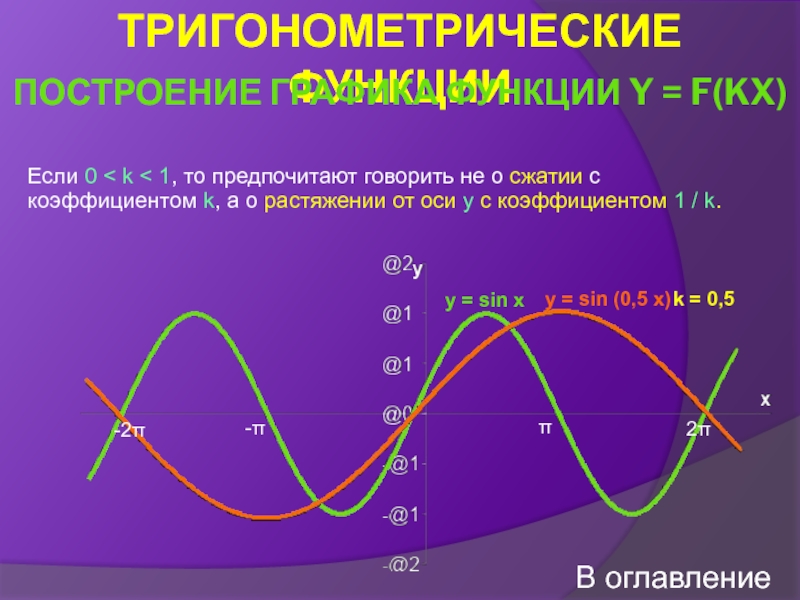
Построение графика функции y = f(kx)
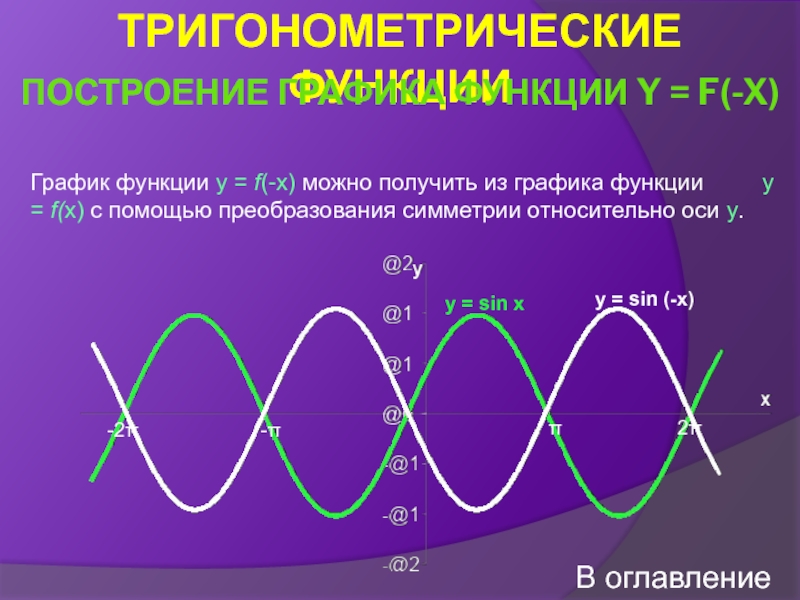
Построение графика функции y = f(-x)
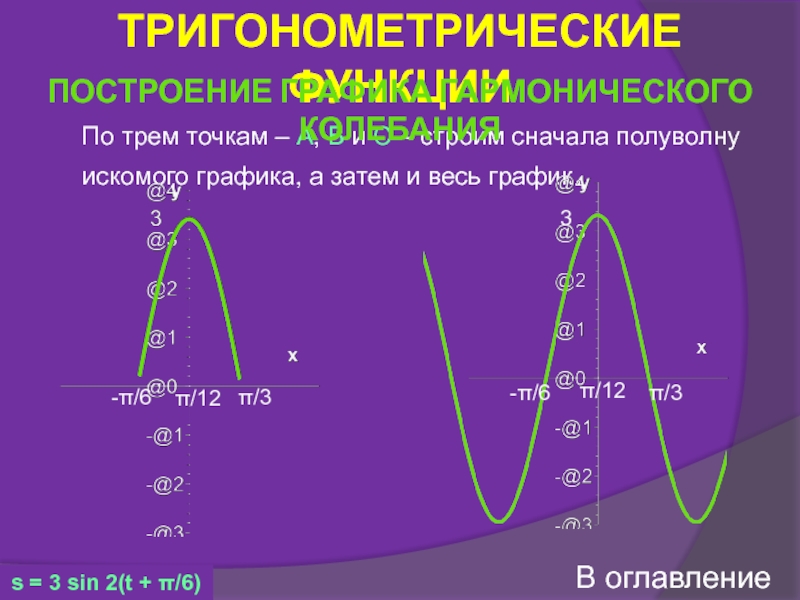
График гармонического колебания
Построение графика гармонического колебания
ОГЛАВЛЕНИЕ





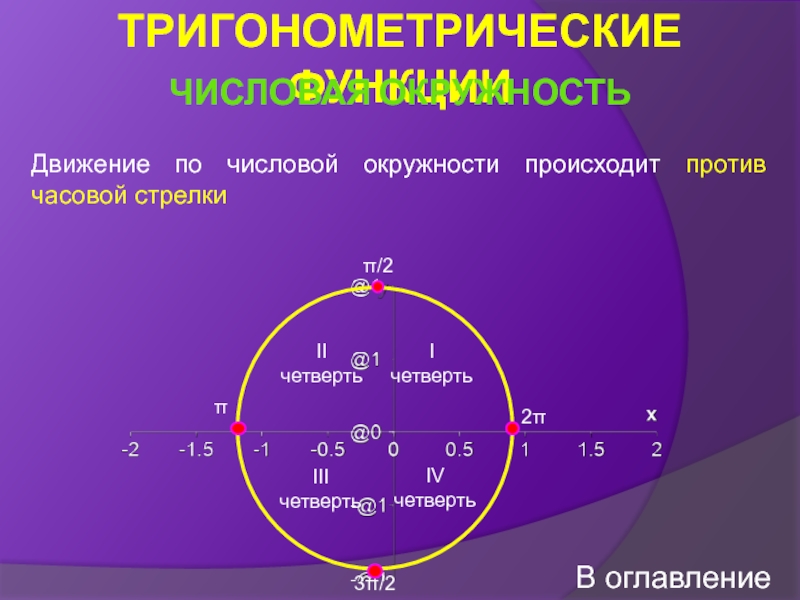
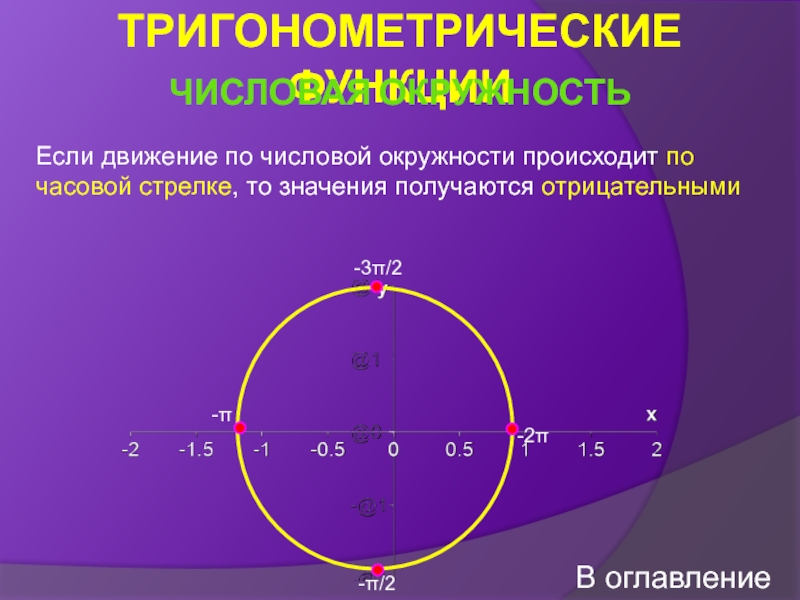






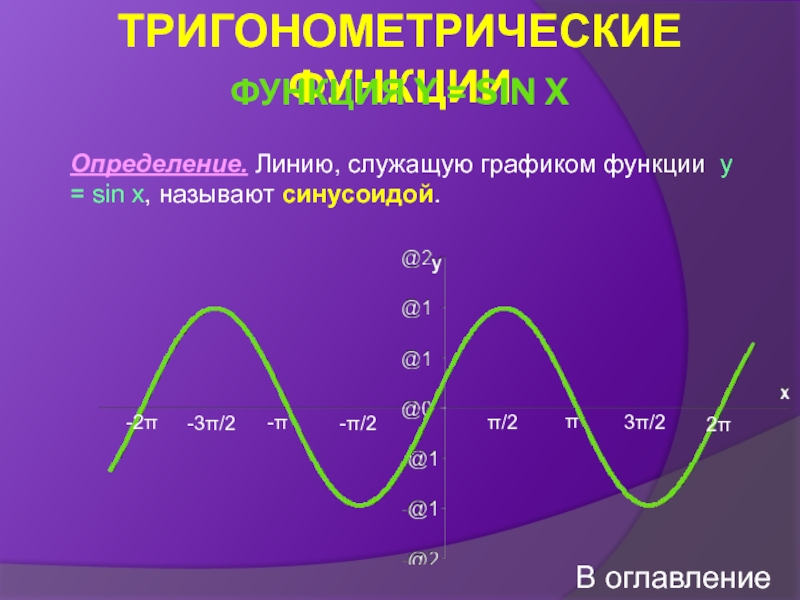


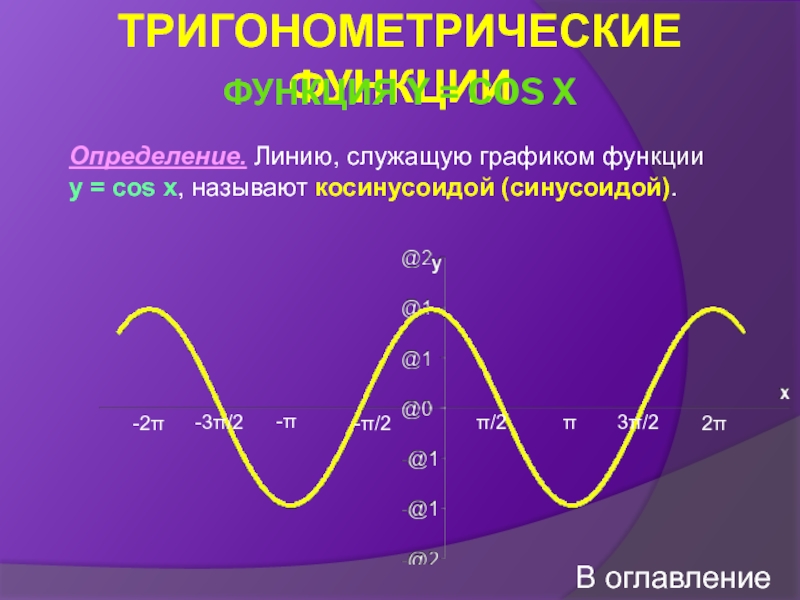












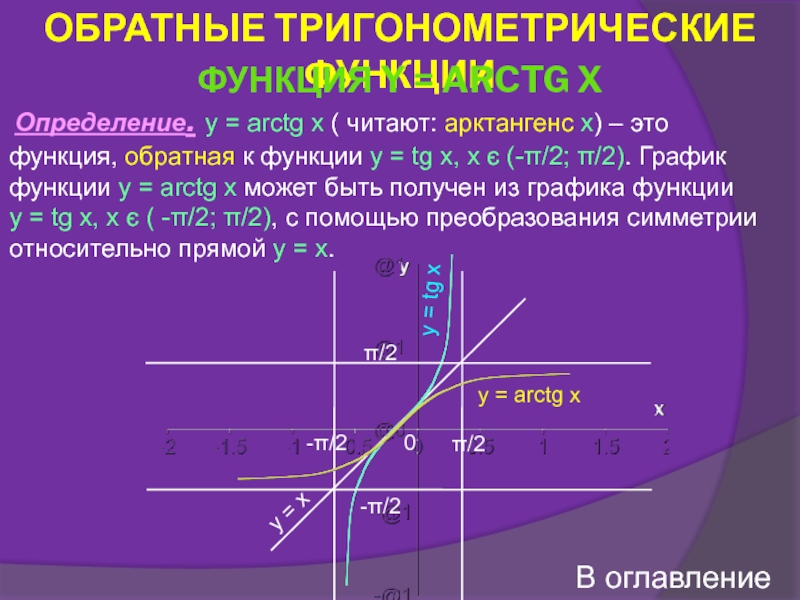
![Тригонометрические функции числового аргумента СВОЙСТВА ФУНКЦИИ Y = ARCSIN X. Свойство 1. D(f) СВОЙСТВА ФУНКЦИИ Y = ARCSIN X. Свойство 1. D(f) = [-1;1].Свойство 2.](/img/thumbs/28707e06c9773b9eac33f94570e30709-800x.jpg)
![Тригонометрические функции числового аргумента Определение. Если |a| ≤ 1, то arcsin a – это Определение. Если |a| ≤ 1, то arcsin a – это такое число из отрезка [-π/2; π/2],](/img/thumbs/72e688cae29655c2db7339c36709a7ba-800x.jpg)
![Тригонометрические функции числового аргумента СВОЙСТВА ФУНКЦИИ Y = ARCCOS X. Свойство 1. D(f) СВОЙСТВА ФУНКЦИИ Y = ARCCOS X. Свойство 1. D(f) = [-1;1].Свойство 2.](/img/thumbs/1af761c8d945c5c419237b10051802b9-800x.jpg)
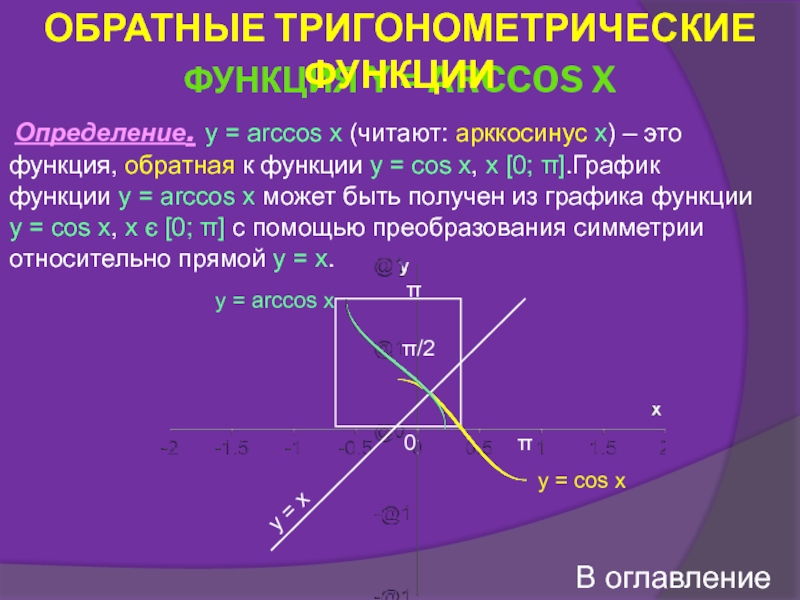
![Тригонометрические функции числового аргумента Определение. Если |a| ≤ 1, то arccos a – это Определение. Если |a| ≤ 1, то arccos a – это такое число из отрезка [0; π],](/img/thumbs/1c6f3a3b4f0d774e4c4db2bc6d627623-800x.jpg)
![Тригонометрические функции числового аргумента Теорема. Для любого a є [-1; 1] выполняется равенство arccos Теорема. Для любого a є [-1; 1] выполняется равенство arccos a + arccos (-a) = π.ОБРАТНЫЕ](/img/thumbs/c108757c1bfd5a74b8067cd7c2bb86be-800x.jpg)