Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение рациональных уравнений
Содержание
- 1. Решение рациональных уравнений
- 2. Проверка домашнего задания Решить уравнения 1-12.
- 3. Проверка домашнего задания Решить уравнения 1-12.
- 4. ВыводыУравнение с одним неизвестным называется запись вида
- 5. Классификация рациональных уравненийВиды уравненийЦелые рациональныеДробно-рациональные Линейные ax=bКвадратные
- 6. Тест
- 7. Тест
- 8. Тест
- 9. Два уравнения называются равносильными, если они имеют
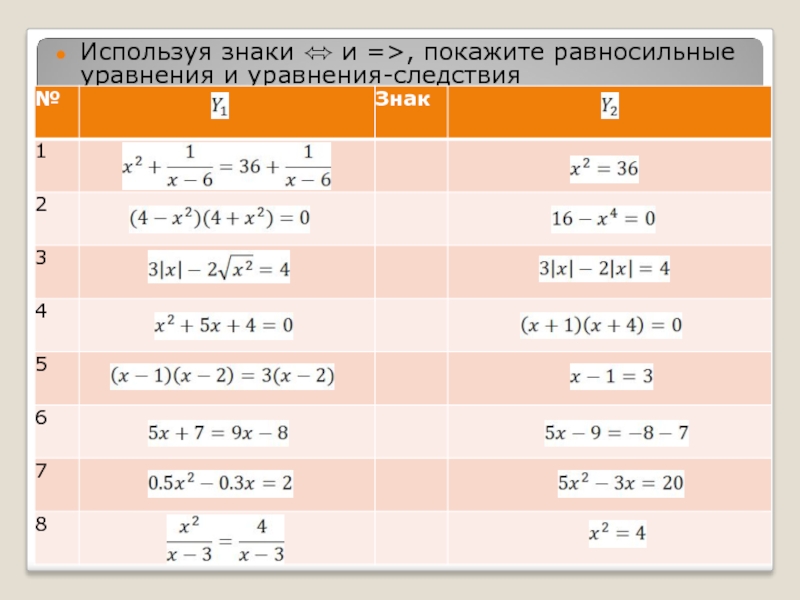
- 10. Используя знаки ⬄ и =>, покажите равносильные уравнения и уравнения-следствия
- 11. Ответы
- 12. ПреобразованияРавносильныеНеравносильныеПростейшие преобразования (6; 7)Преобразования, связанные с применением
- 13. Решить уравнение
- 14. РешениеСпособ 1. Применение преобразований, равносильных на множестве.Ответ: -4
- 15. РешениеСпособ 2. Переход к следствиям.Проверка: для найденных значений при выполнении условия1.2.Ответ: -4
- 16. Выводы:Если исходное уравнение преобразуется в равносильное уравнение,
- 17. Скачать презентанцию
Проверка домашнего задания Решить уравнения 1-12.
Слайды и текст этой презентации
Слайд 4Выводы
Уравнение с одним неизвестным называется запись вида A(x)=B(x), в которой
A(x) и B(x) – выражение от неизвестной x.
Областью определения уравнения
называется множество всех значений x, при которых определены обе части уравнения.Корнем или решением уравнения называется значение неизвестного, при подстановке которого в уравнение получается верное числовое равенство.
Решить уравнение –значит найти все корни или доказать, что их нет
Слайд 5
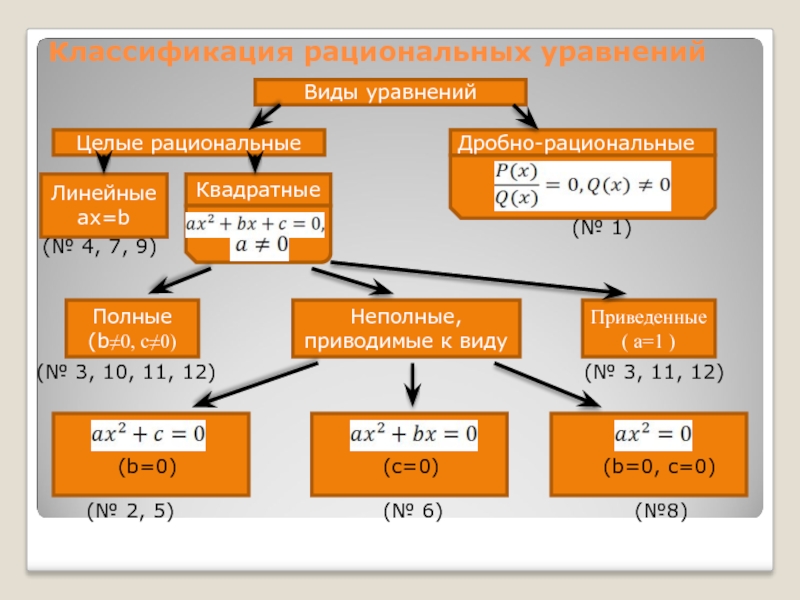
Классификация рациональных уравнений
Виды уравнений
Целые рациональные
Дробно-рациональные
Линейные ax=b
Квадратные
(№ 4, 7,
9)
(№ 1)
Полные (b≠0, c≠0)
(№ 3, 10, 11, 12)
Неполные, приводимые к
видуПриведенные( a=1 )
(№ 3, 11, 12)
(b=0)
(c=0)
(b=0, c=0)
(№ 2, 5)
(№ 6)
(№8)
Слайд 9Два уравнения называются равносильными, если они имеют одинаковые корни или
если оба уравнения не имеют корней
Уравнение называется следствием уравнения
, если любой корень является корнем
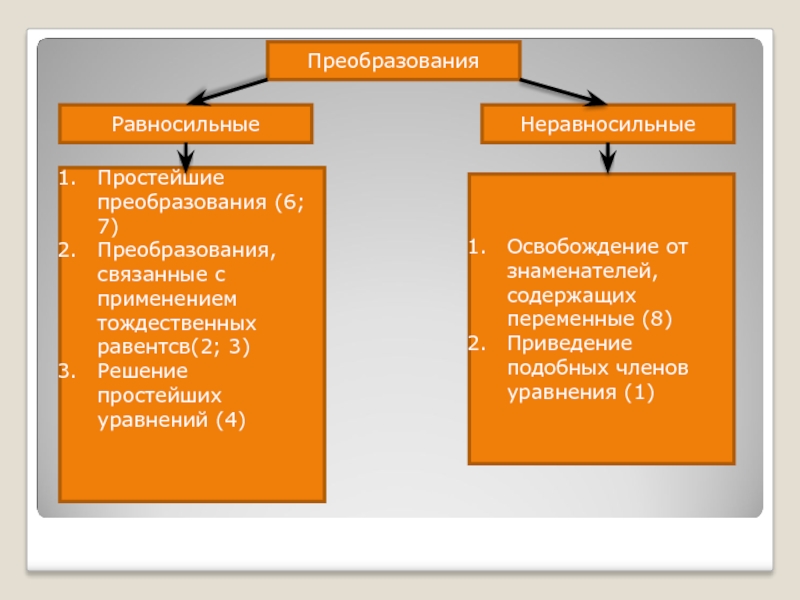
Слайд 12Преобразования
Равносильные
Неравносильные
Простейшие преобразования (6; 7)
Преобразования, связанные с применением тождественных равентсв(2; 3)
Решение
простейших уравнений (4)
Освобождение от знаменателей, содержащих переменные (8)
Приведение подобных членов
уравнения (1)Слайд 15Решение
Способ 2. Переход к следствиям.
Проверка: для найденных значений при выполнении
условия
1.
2.
Ответ: -4
Слайд 16Выводы:
Если исходное уравнение преобразуется в равносильное уравнение, то никакой особой
проверки решения уравнения не требуется.
Если же исходное уравнение преобразуется в
процессе решения уравнение-следствие, то обязательна проверка всех найденных уравнений
Теги