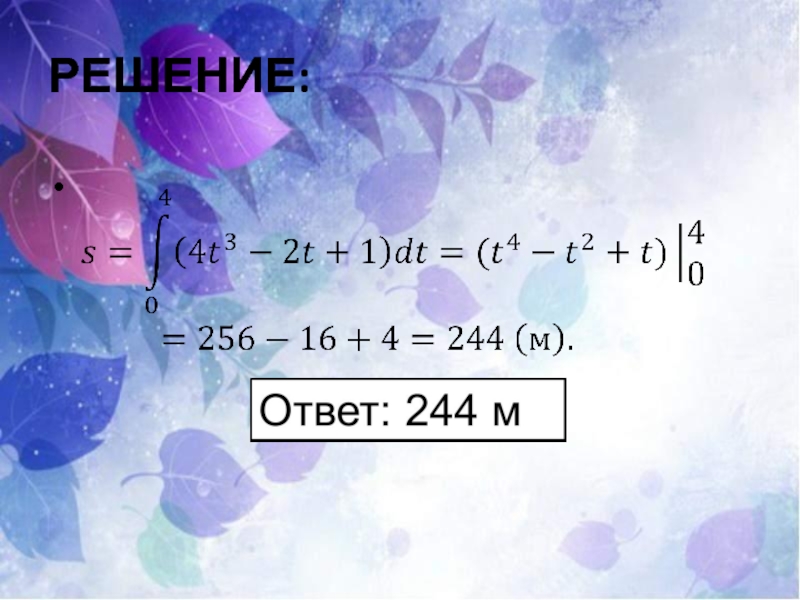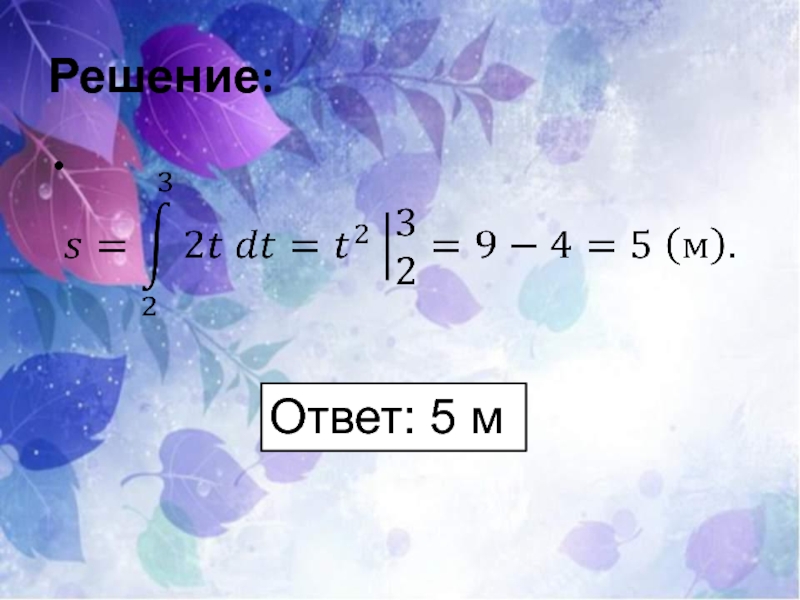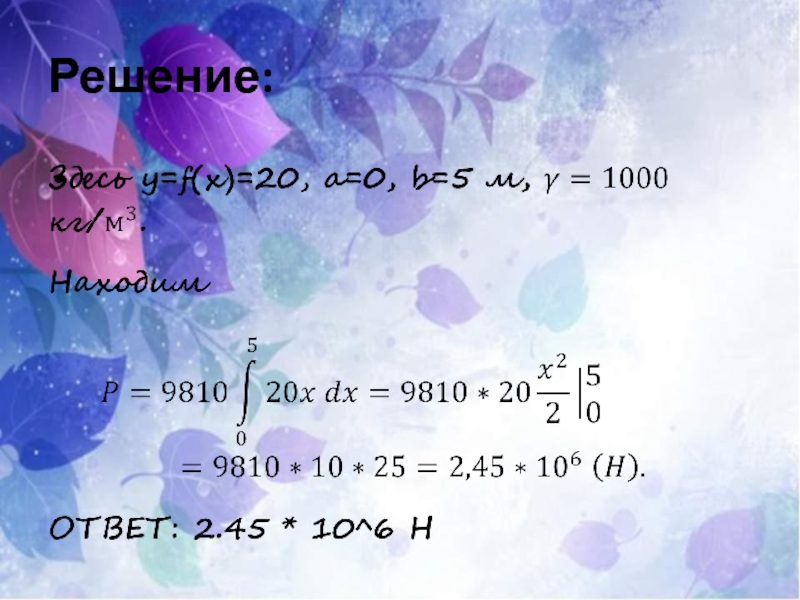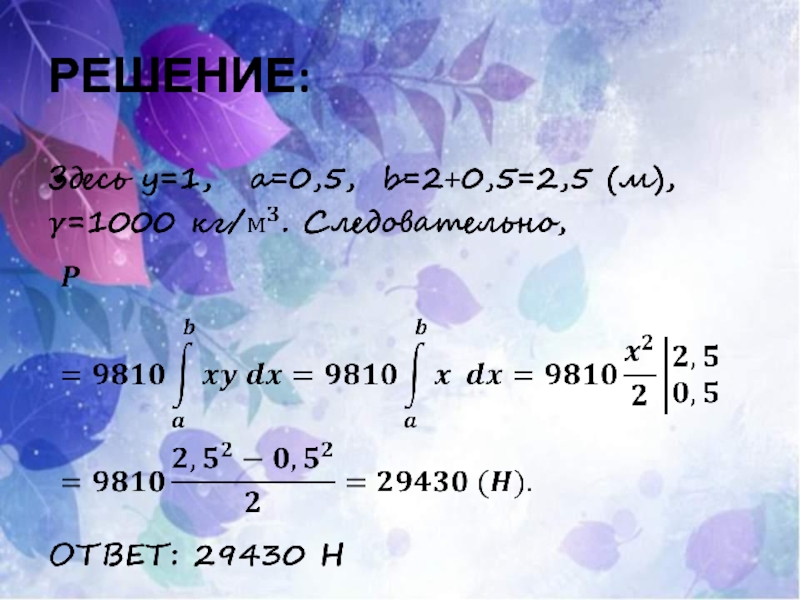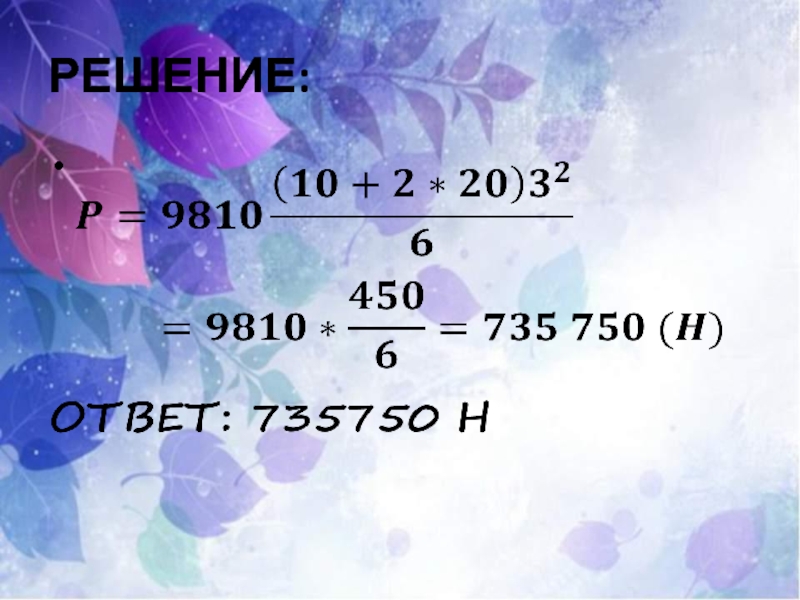Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение интеграла к решению физических задач 11 класс
Содержание
- 1. Применение интеграла к решению физических задач 11 класс
- 2. Цели урока: обобщить и закрепить ключевые задачи
- 3. Повторение основных понятий:2. Что вы знаете о
- 4. План урока:1. Схема решения задач на приложения
- 5. Рассмотрим теорию по данной теме
- 6. 1. Схема решения задач на приложения определенного
- 7. 2. Нахождение пути, пройденного телом при прямолинейном
- 8. 3. Вычисление работы силы, произведенной при прямолинейном движении тела
- 9. 4.Вычисление работы, затраченной на растяжение или сжатие пружины
- 10. 5.Определение силы давления жидкости на вертикально расположенную пластинку
- 11. Слайд 11
- 12. Рассмотрим примеры задач по данной теме № 1
- 13. РЕШЕНИЕ:
- 14. № 2
- 15. Решение: Ответ: 5 м
- 16. № 3
- 17. Решение: Ответ: 32 м
- 18. № 4
- 19. Решение: Ответ: 44,1 м
- 20. № 5Какую работу совершает сила в 10Н при растяжении пружины на 2 см?
- 21. Решение:
- 22. № 6Сила в 60Н растягивает пружину на
- 23. Решение:
- 24. № 7Определить силу давления воды на стенку
- 25. Решение:
- 26. № 8В воду опущена прямоугольная пластинка, расположенная
- 27. РЕШЕНИЕ:
- 28. № 9
- 29. РЕШЕНИЕ:
- 30. № 10
- 31. РЕШЕНИЕ:
- 32. № 11
- 33. РЕШЕНИЕ:
- 34. № 12Вычислить силу давления воды на плотину,
- 35. РЕШЕНИЕ:
- 36. № 13
- 37. РЕШЕНИЕ:
- 38. Скачать презентанцию
Цели урока: обобщить и закрепить ключевые задачи по теме научиться работать с теоретическими вопросами темы научиться применять интеграл к решению физических задач
Слайды и текст этой презентации
Слайд 2Цели урока:
обобщить и закрепить ключевые задачи по теме
научиться
работать с теоретическими вопросами темы
физических задачСлайд 3Повторение основных понятий:
2. Что вы знаете о интеграле (свойства, теоремы)?
1.
Скажите основное определение интеграла?
3. Знаете ли вы какие-нибудь примеры задач
с применением интеграла?Слайд 4План урока:
1. Схема решения задач на приложения определенного интеграла
2. Нахождение
пути, пройденного телом при прямолинейном движении
3. Вычисление работы силы, произведенной
при прямолинейном движении тела4. Вычисление работы, затраченной на растяжение или сжатие пружины
5. Определение силы давления жидкости на вертикально расположенную пластинку
Слайд 61. Схема решения задач на приложения определенного интеграла
С помощью определенного
интеграла можно решать различные задачи физики, механики и т. д.,
которые трудно или невозможно решить методами элементарной математики.Так, понятие определенного интеграла применяется при решении задач на вычисление работы переменной силы, давления жидкости на вертикальную поверхность, пути, пройденного телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они объединяются одной и той же схемой рассуждений при их решении. Искомая величина (путь, работа, давление и т. д.) соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную величину обозначают через Х, а промежуток ее изменения — через [а, b].
Отрезок [a, b] разбивают на n равных частей, в каждой из которых можно пренебречь изменением переменной величины. Этого можно добиться при увеличении числа разбиений отрезка.
На каждой такой части задачу решают
по формулам для постоянных величин.
Далее составляют сумму (интегральную
сумму), выражающую приближенное
значение искомой величины. Переходя к
пределу при n→∞, находят искомую
величину I в виде интеграла
Слайд 72. Нахождение пути, пройденного телом при прямолинейном движении
Как известно, путь,
пройденный телом при равномерном движении за время t, вычисляется по
формуле S=vt.Если тело движется неравномерно в одном направлении и скорость его меняется в зависимости от времени t, т. е. v=f(t), то для нахождения пути, пройденного телом за время от t1 до t2, разделим этот промежуток времени на n равных частей Δt. В каждой из таких частей скорость можно считать постоянной и равной значению скорости в конце этого промежутка. Тогда пройденный телом путь будет приблизительно равен сумме: