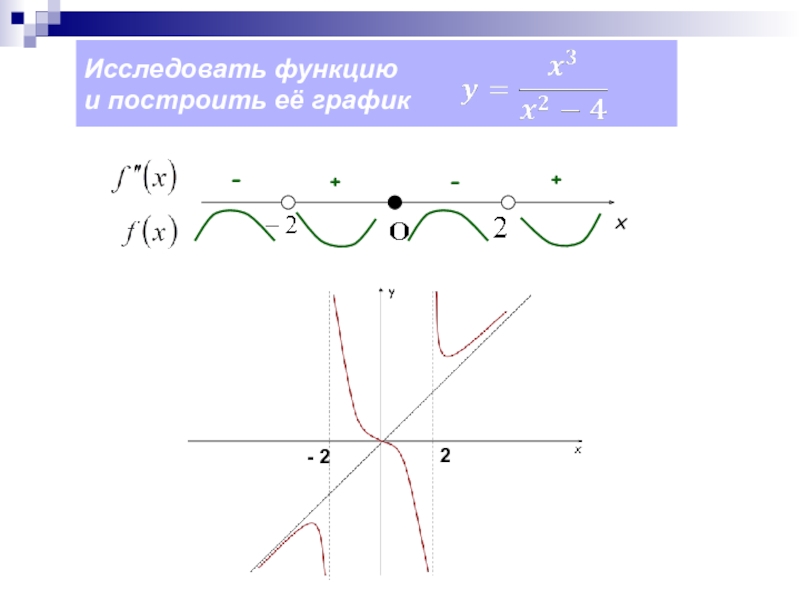
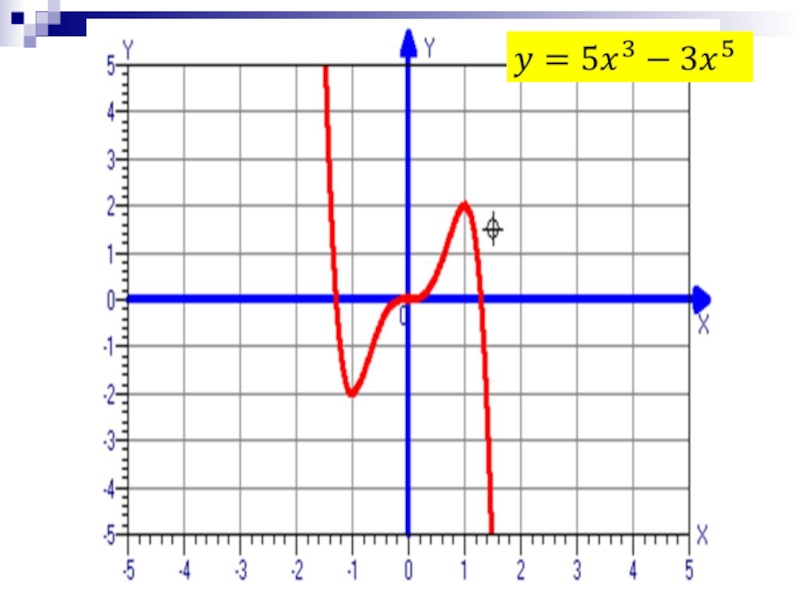
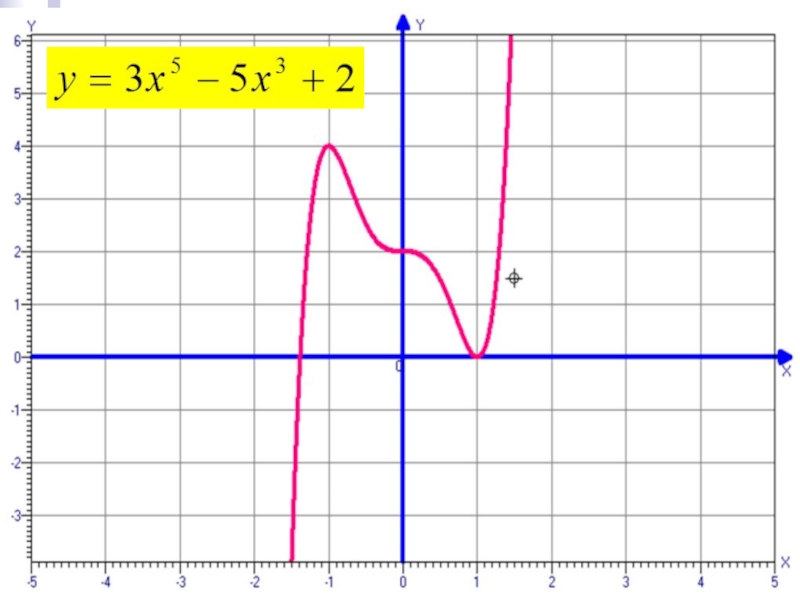
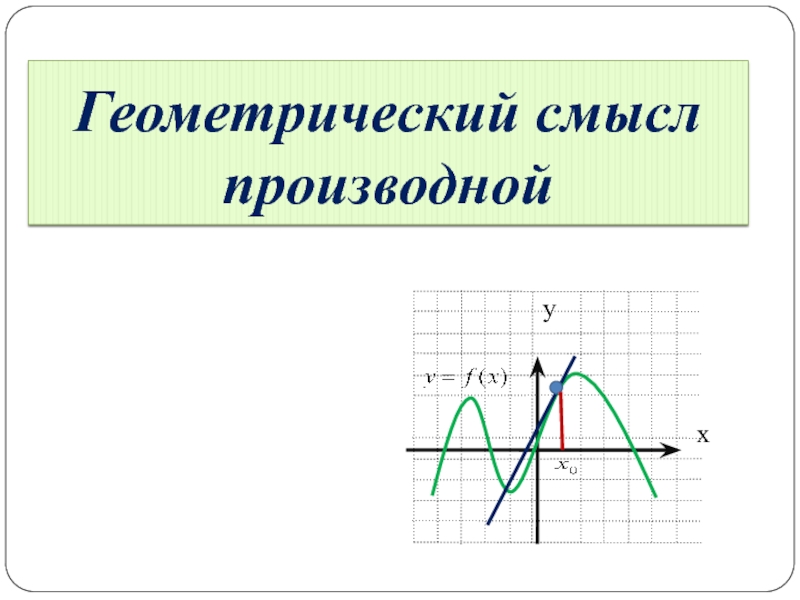
расширить алгоритм исследования функции;
оценить свои знания по теме;
развивать умение
работать в паре;развивать логическое мышление;
формировать навыки
контроля и самоконтроля.