Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Степенные функции, их свойства и графики 11 класс
Содержание
- 1. Степенные функции, их свойства и графики 11 класс
- 2. Заголовок слайдаФункция вида у = хr (где
- 3. Слайд 3
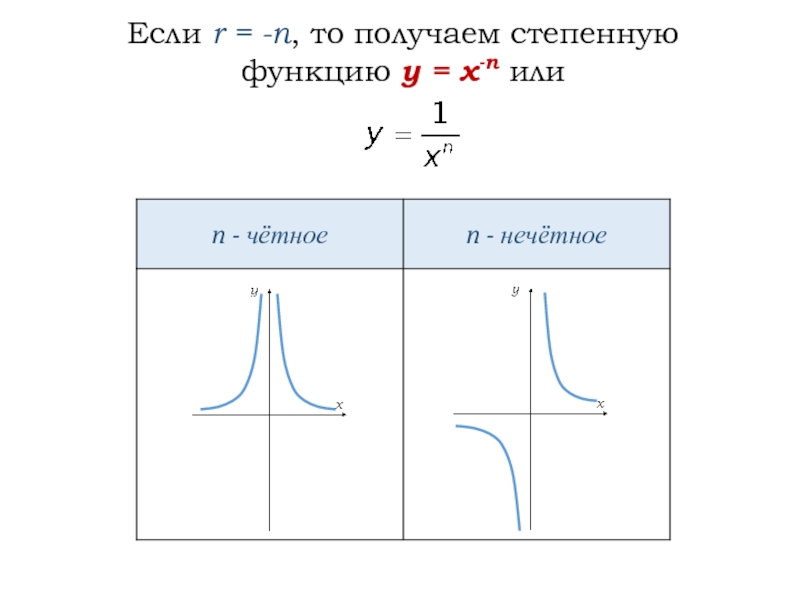
- 4. Если r = -n, то получаем степенную функцию y = x-n или
- 5. При r = 0 имеем функцию y
- 6. Рассмотрим теперь степенные функцииС рациональными показателями степени.Их свойства и графики существенно зависят от показателя степени.
- 7. Область определения D(f) = [0; +∞).Определённой чётности
- 8. Область определения D(f) = [0; +∞).Определённой чётности
- 9. Область определения D(f) = (0; +∞).Определённой чётности
- 10. Теорема. Если х>0 и r – любое
- 11. Пример 1.Найдём производную функции:При этом было использовано правило дифференцирования
- 12. Пример 2.Исследуем функциюНа монотонность и экстремумы и
- 13. 4. График функции у(х) пересекает ось абсцисс
- 14. Пример 3.Напишем уравнение касательной к графику функции
- 15. Контрольные вопросы:1. Определение степенной функции у =
- 16. http://school-box.ru/raznoe/vse-dlya-prezentazii/1486-shablony-dlya-prezentaziy-powerpoint-21.html Шаблон презентации:http://dg54.mycdn.me/getImage?photoId=582860090169&photoType=6 Эмблема СУПа:•Мордкович А.Г. -
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Урок алгебры в 11 классе
Степенные функции,
их свойства и графики.
Подготовила
Учитель
математики
Слайд 2Заголовок слайда
Функция вида у = хr (где r - любое
действительное число (в том числе и иррациональное)) называют
степенными функциями.
Если
r - натуральное число (r = n), то получаем функцию y = xn.Слайд 5При r = 0 имеем функцию y = x0 или
у = 1
(где х ≠ 0). Графиком такой функции
является горизонтальная прямая у = 1 с выколотой точкой х = 0 (х>0).
1
Слайд 6Рассмотрим теперь степенные функции
С рациональными показателями степени.
Их свойства и графики
существенно зависят от показателя степени.
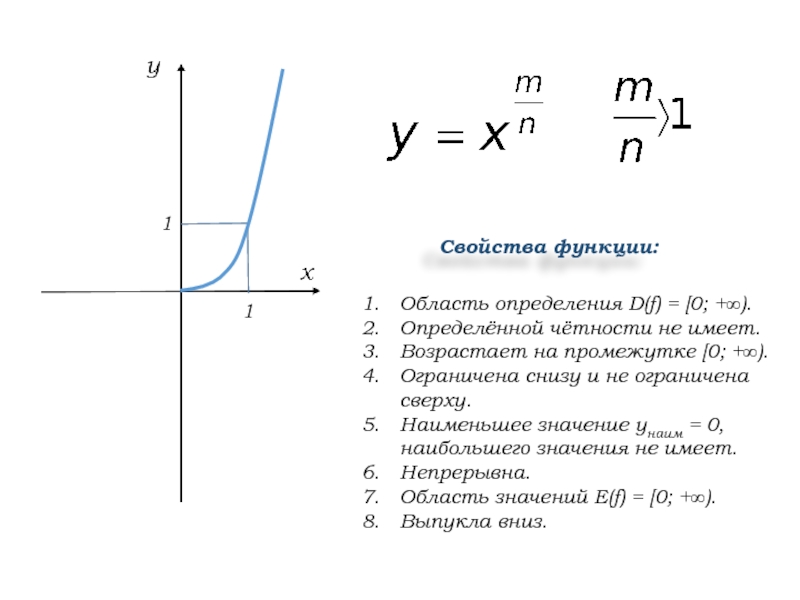
Слайд 7Область определения D(f) = [0; +∞).
Определённой чётности не имеет.
Возрастает на
промежутке [0; +∞).
Ограничена снизу и не ограничена сверху.
Наименьшее значение унаим
= 0, наибольшего значения не имеет.Непрерывна.
Область значений Е(f) = [0; +∞).
Выпукла вниз.
Свойства функции:
1
1
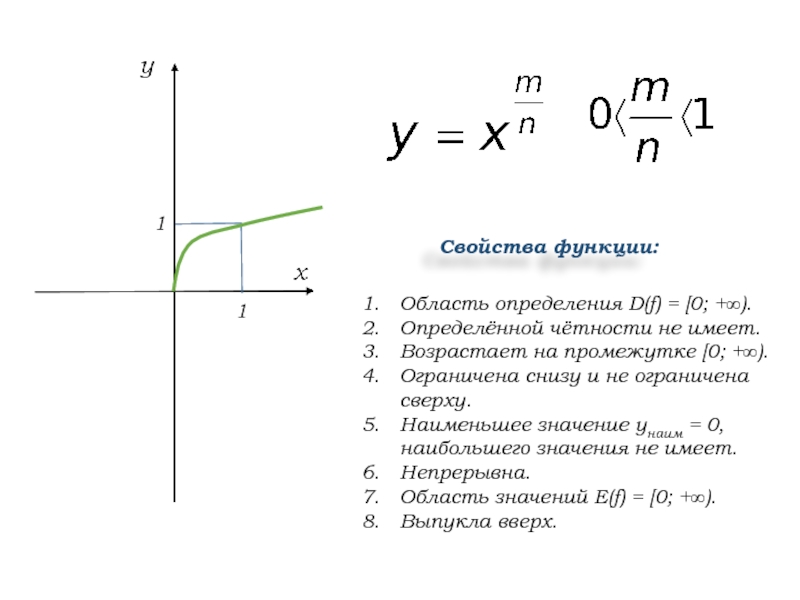
Слайд 8Область определения D(f) = [0; +∞).
Определённой чётности не имеет.
Возрастает на
промежутке [0; +∞).
Ограничена снизу и не ограничена сверху.
Наименьшее значение унаим
= 0, наибольшего значения не имеет.Непрерывна.
Область значений Е(f) = [0; +∞).
Выпукла вверх.
Свойства функции:
1
1
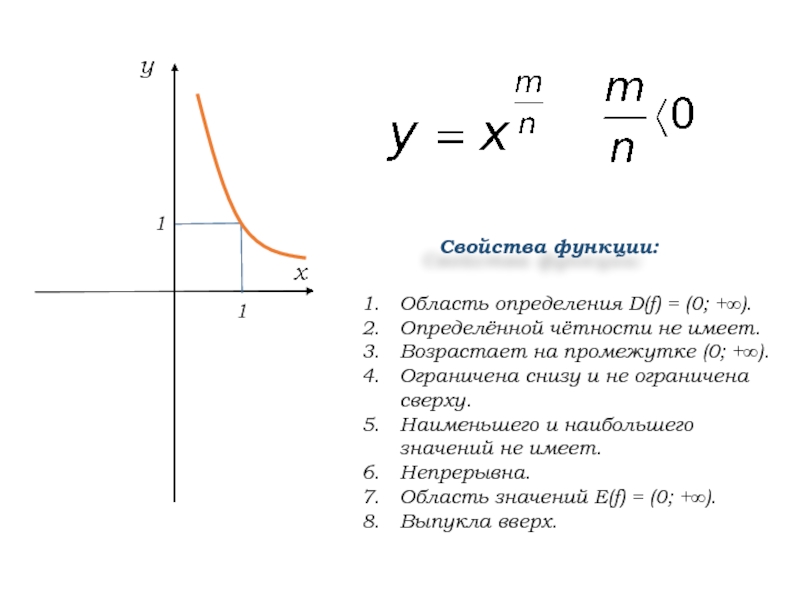
Слайд 9Область определения D(f) = (0; +∞).
Определённой чётности не имеет.
Возрастает на
промежутке (0; +∞).
Ограничена снизу и не ограничена сверху.
Наименьшего и наибольшего
значений не имеет.Непрерывна.
Область значений Е(f) = (0; +∞).
Выпукла вверх.
Свойства функции:
1
1
Слайд 10Теорема.
Если х>0 и r – любое рациональное число, то
производная степенной функции y = xr вычисляется по формуле
Слайд 12Пример 2.
Исследуем функцию
На монотонность и экстремумы и
построим её график.
1.
Найдём производную функции:
2. Функция существует при х ≥ 0, производная
существует при х>0. Поэтому критических точек у функции нет. Стационарную точку найдём из условия или , откуда х=1.3. Очевидно, что при х (0;1], значение у'≤0 и функция у(х) убывает на этом промежутке. При х [1;+∞) значение у'≥0 и функция у(х) возрастает. В точке х = 1 функция у(х) имеет минимум
э
э
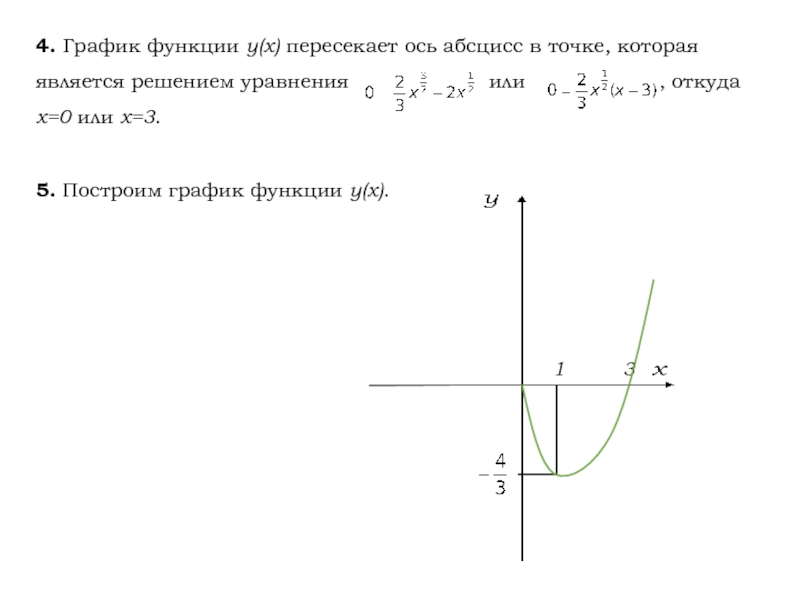
Слайд 134. График функции у(х) пересекает ось абсцисс в точке, которая
является решением уравнения
или , откудах=0 или х=3.
5. Построим график функции у(х).
1
3
Слайд 14Пример 3.
Напишем уравнение касательной к графику функции
в точке а
= 1.Напомним общий вид уравнения касательной: y = f(a) + f‘(a)(x-a)
1. Найдём значение функции:
2. Найдём производную функции:
и её значение .
3. Подставим значения f(a), f'(a) и а в уравнение касательной и получим:
Слайд 15Контрольные вопросы:
1. Определение степенной функции у = хr.
2. Свойства функции
и её график
для:3. Производная степенной функции.
Слайд 16http://school-box.ru/raznoe/vse-dlya-prezentazii/1486-shablony-dlya-prezentaziy-powerpoint-21.html
Шаблон презентации:
http://dg54.mycdn.me/getImage?photoId=582860090169&photoType=6
Эмблема СУПа:
•Мордкович А.Г. - учебник-Алгебра и начала
математического анализа(10-11, ч.1, баз.ур.)-2014
•Мордкович А.Г. - задачник-Алгебра и начала математического
анализа (10-11 кл., ч.2, баз.ур.) -2014Источники: