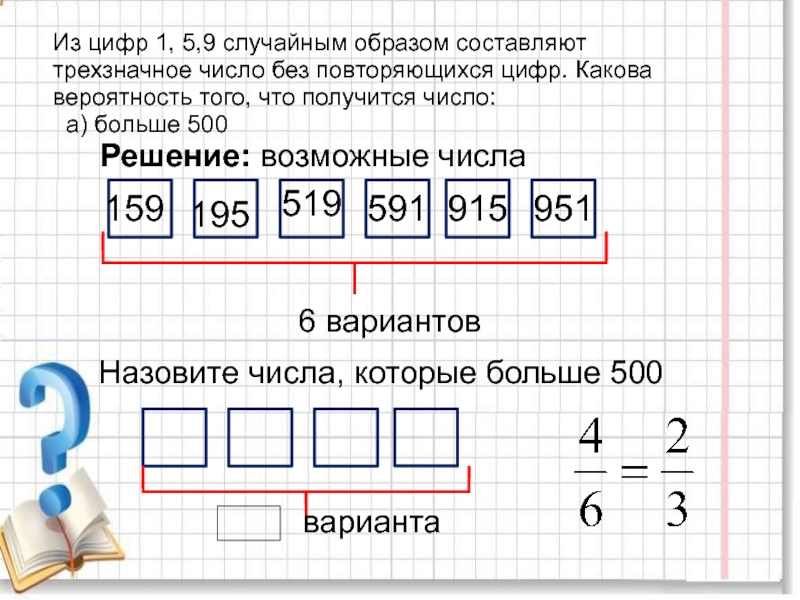
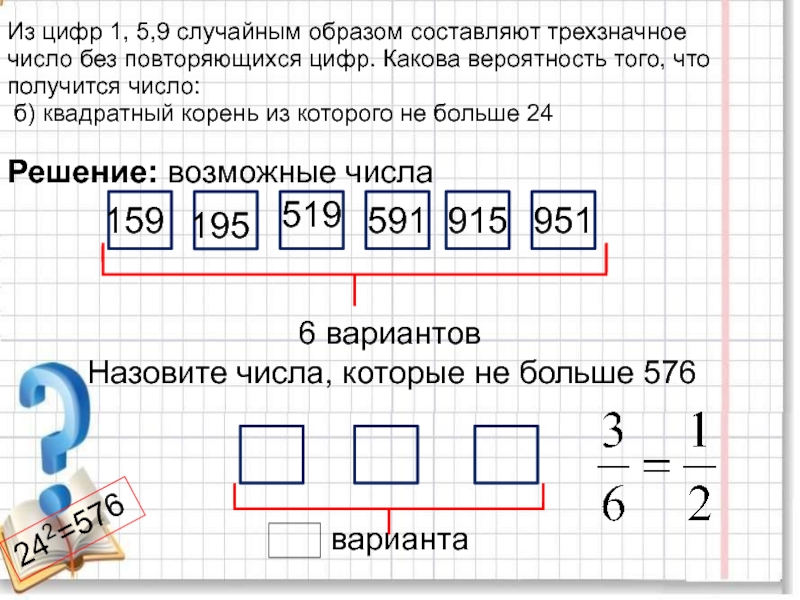
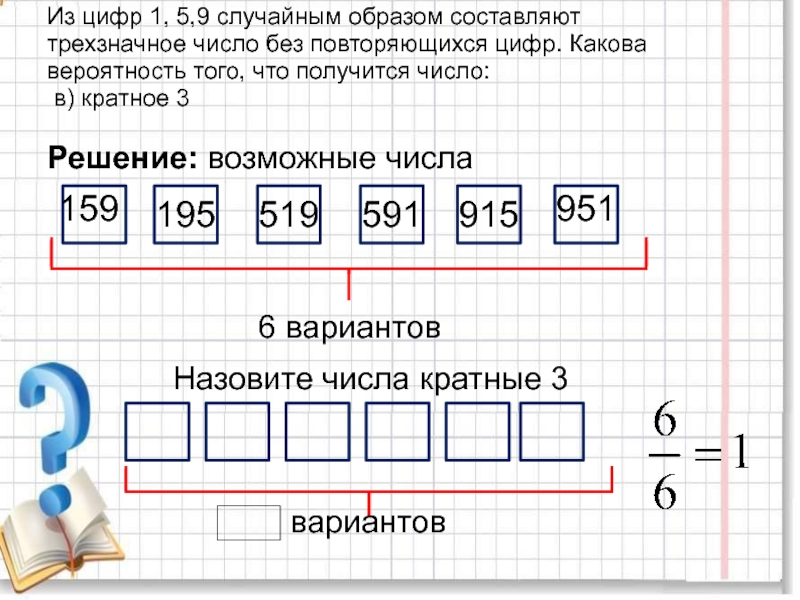
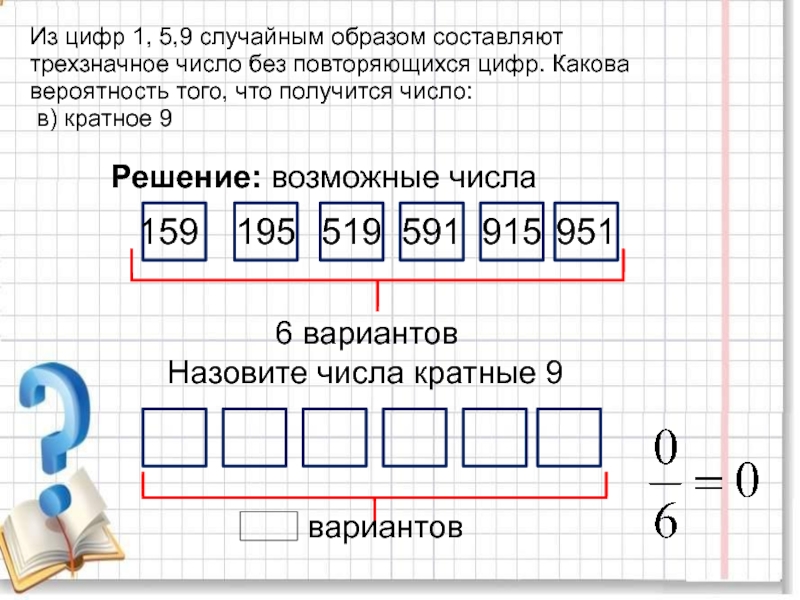
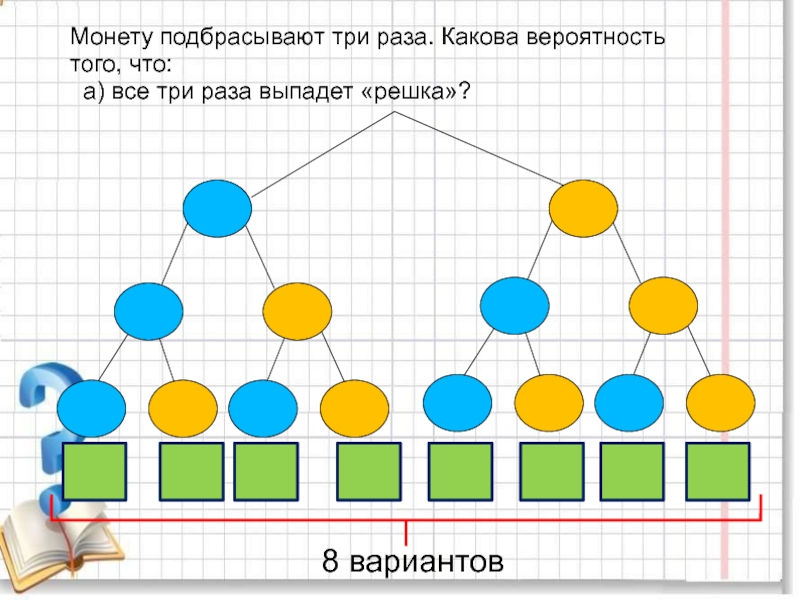
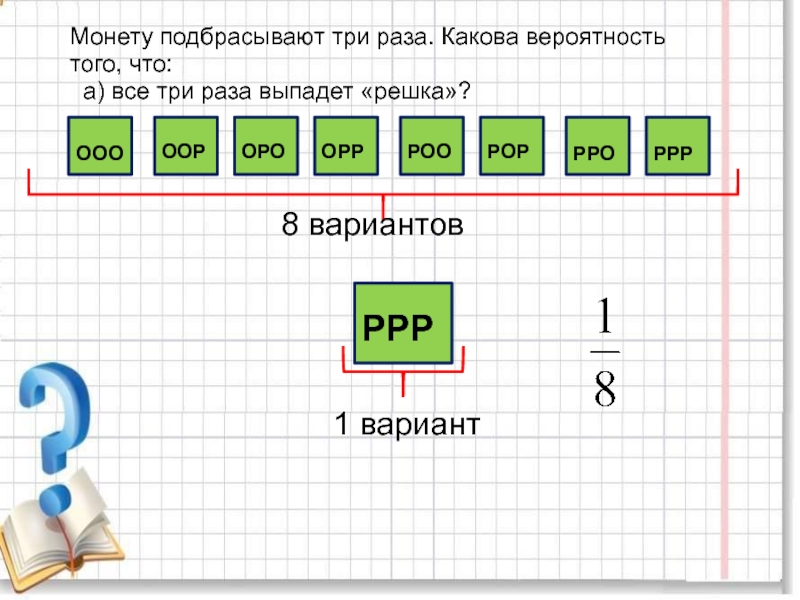
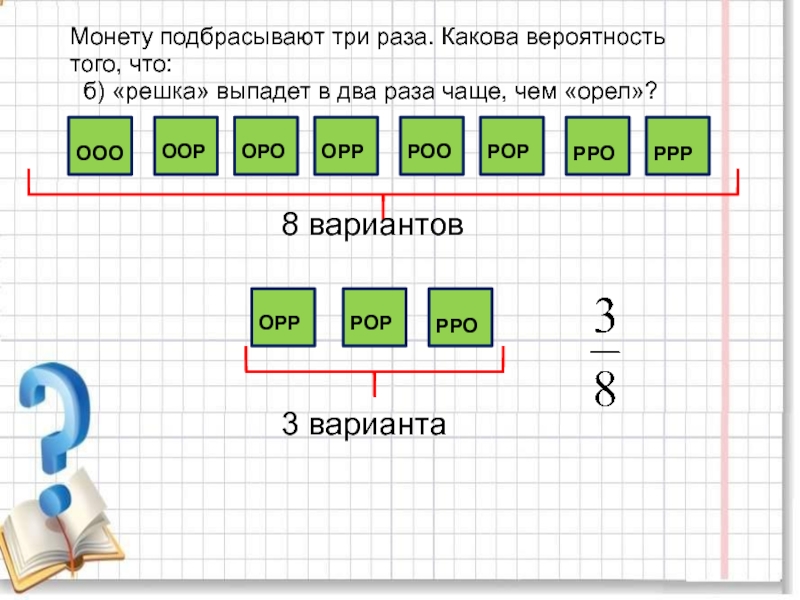
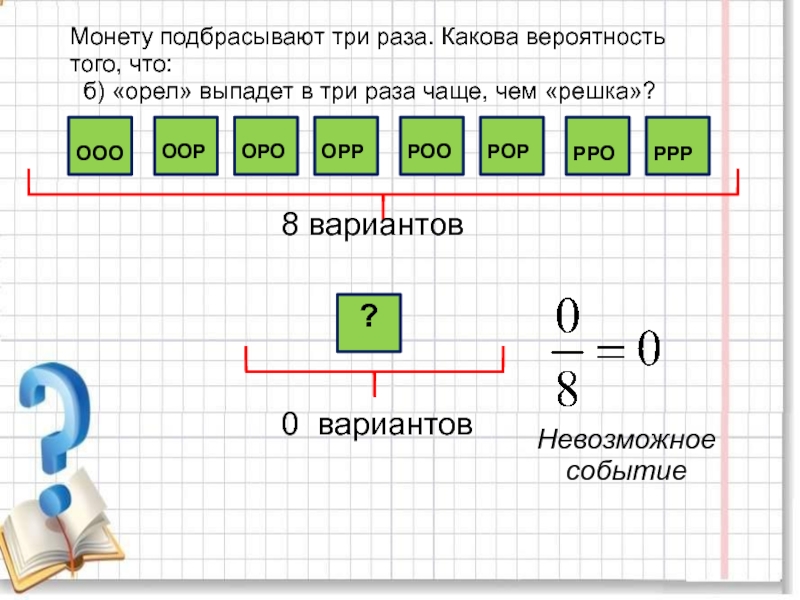
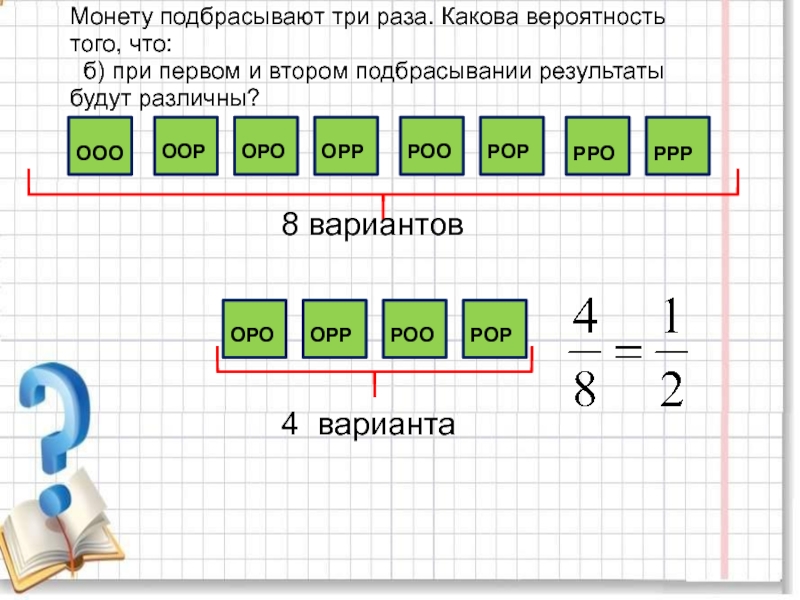
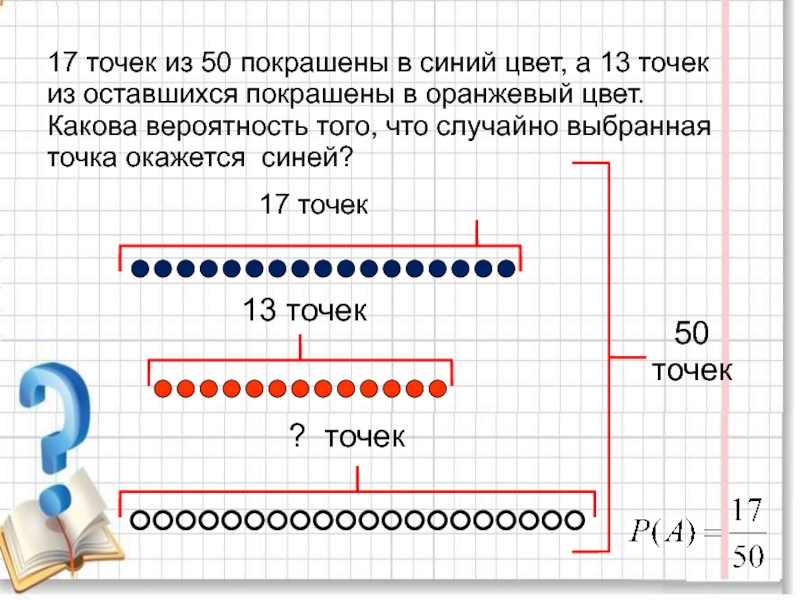
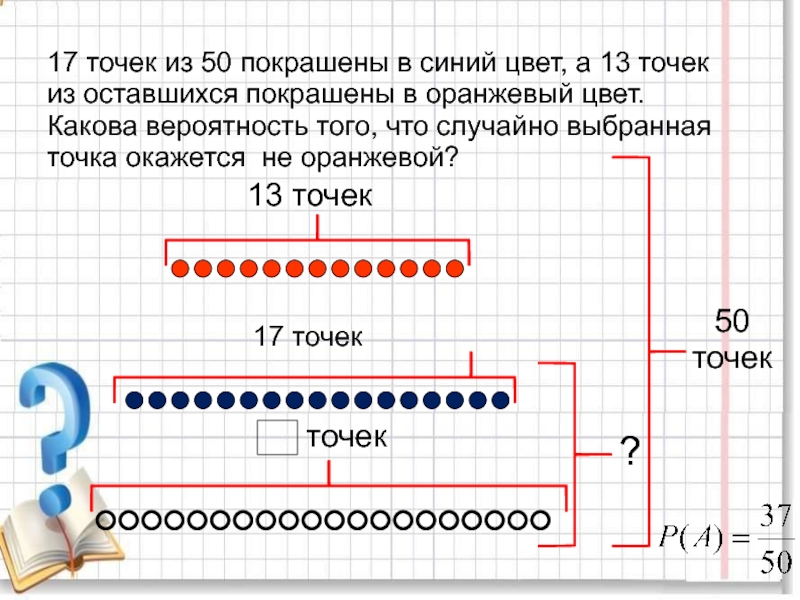
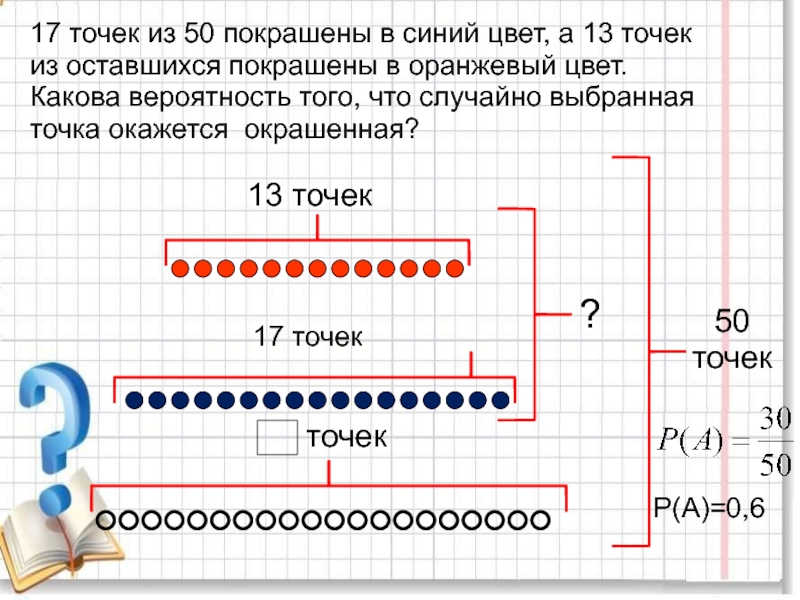
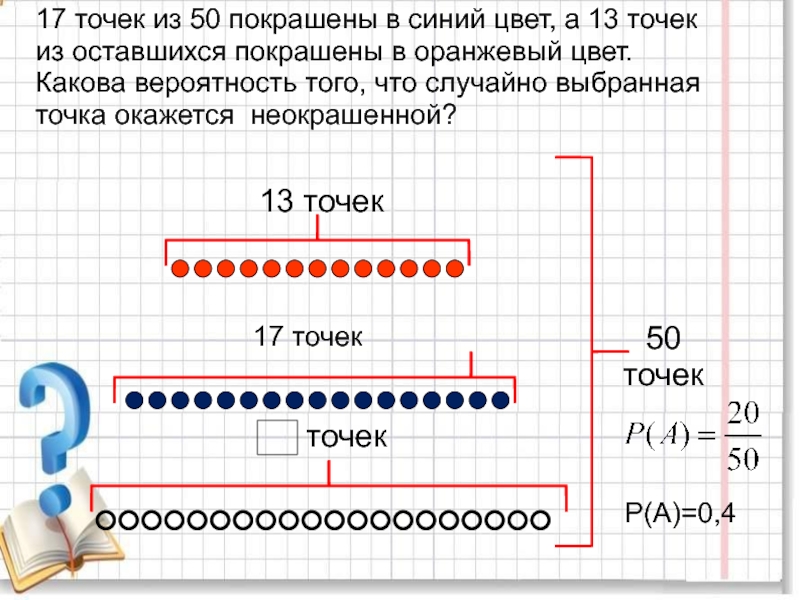
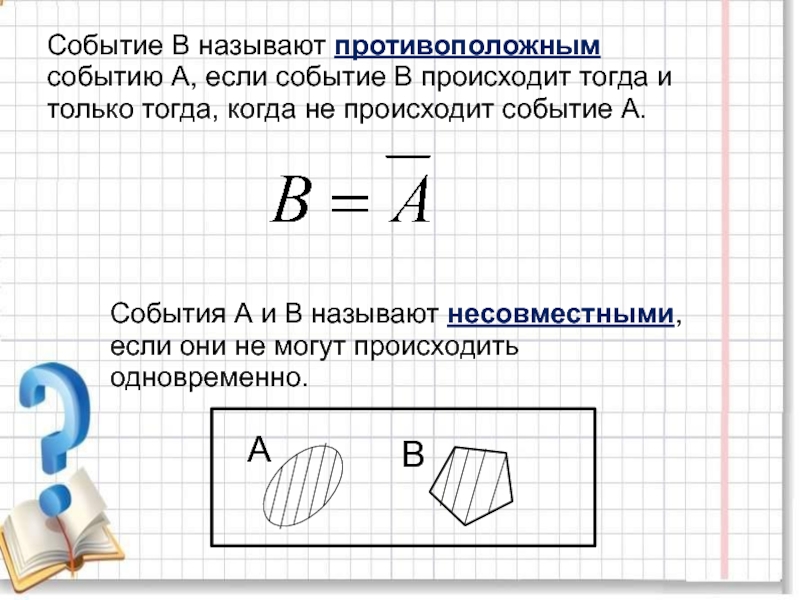
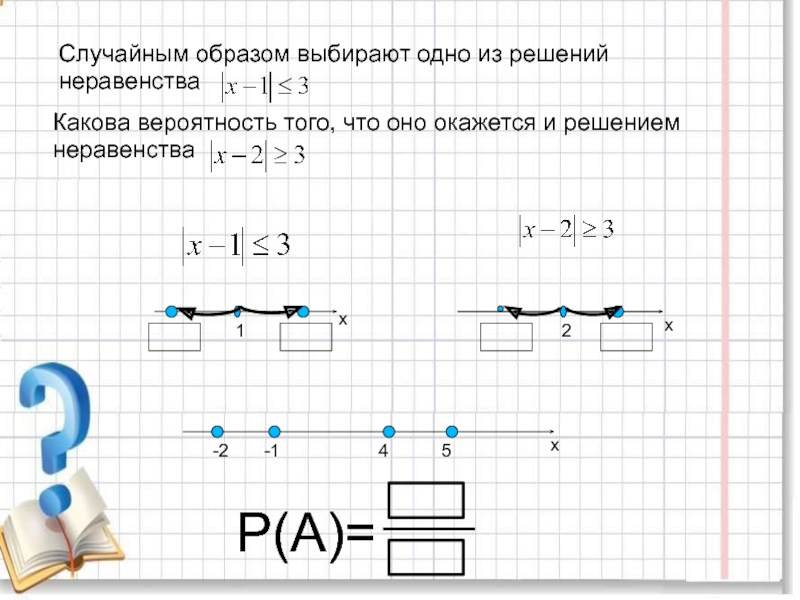
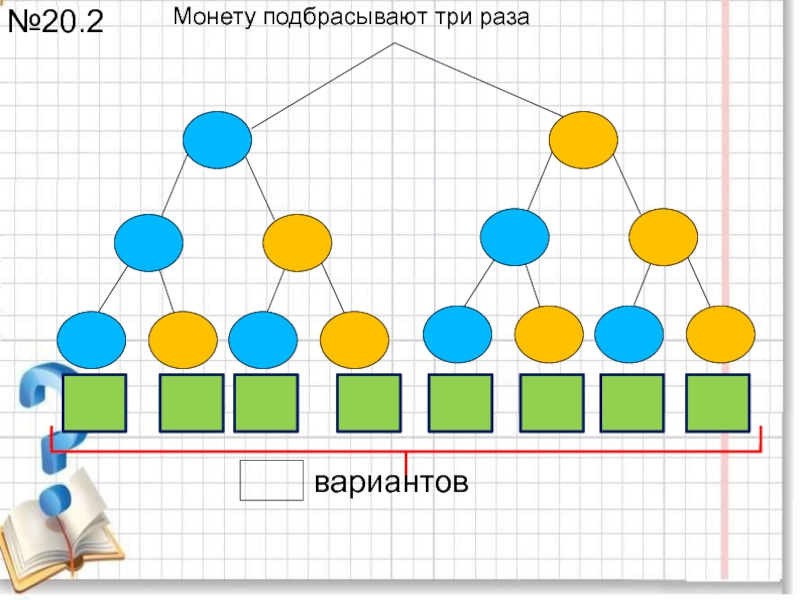
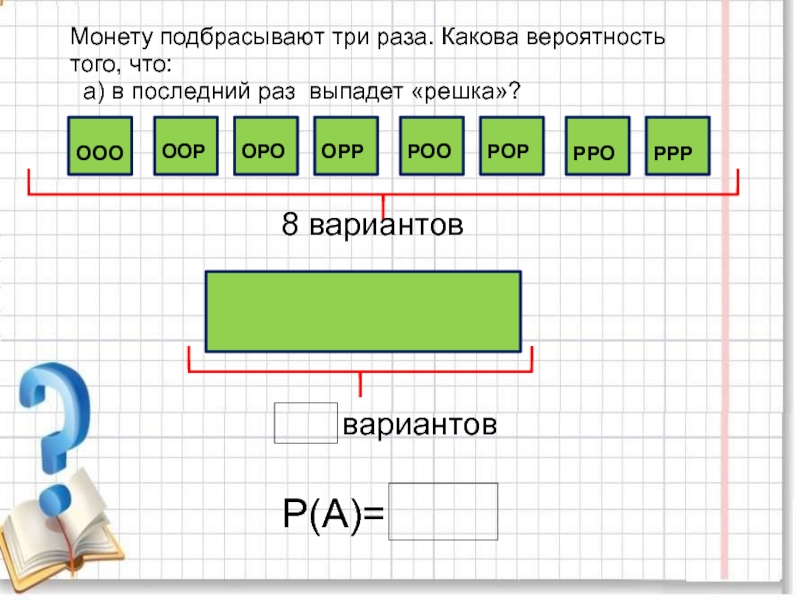
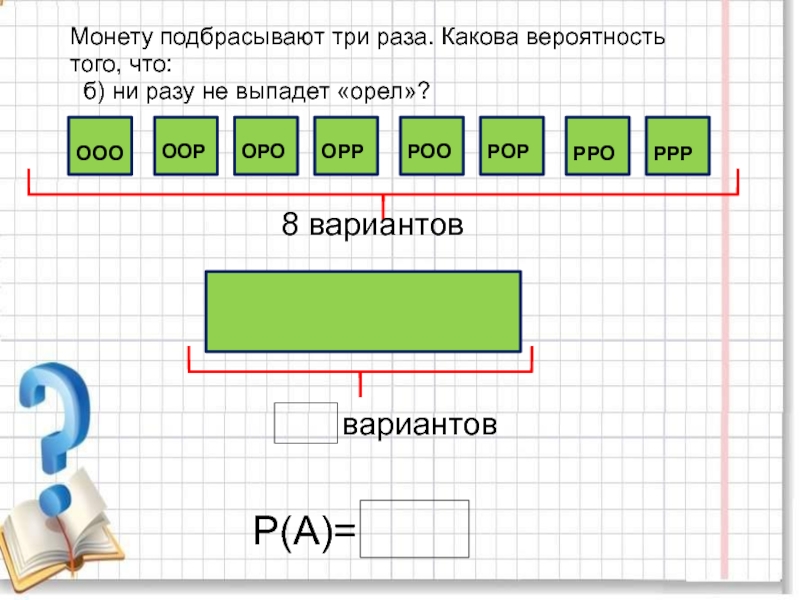
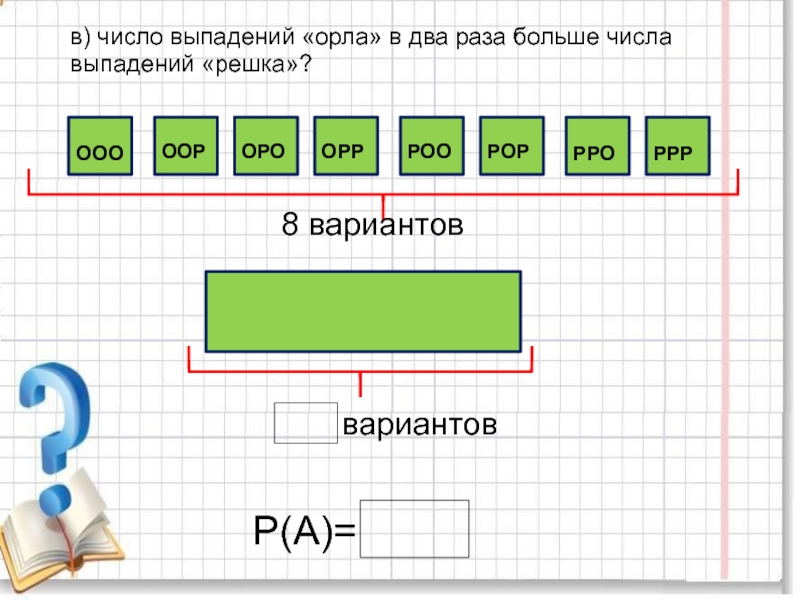
повторяющихся цифр. Какова вероятность того, что получится число:
а) больше
500б) квадратный корень из которого не больше 24
в) кратное 3
г) кратное 9
Решение:
Напишите возможные числа, составленные из цифр 1,5,9