Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синус и косинус 10 класс
Содержание
- 1. Синус и косинус 10 класс
- 2. Синус и косинус.Что будем повторять ,что будем
- 3. Определение.Синус и косинус.Ребята, давайте отметим на числовой
- 4. Тангенс и котангенс.Отношение синуса числа t к косинусу того
- 5. Синус и косинус.Основное тригонометрическое тождество.Давайте вспомним уравнение
- 6. Таблица значений синуса, косинуса, тангенса, котангенса.Синус и
- 7. Основные свойства.Синус и косинус.Для любого числа t
- 8. Синус и косинус.Синус и косинус в жизни.Для
- 9. ПримерВычислить синус и косинус t при: t=53π/4Решение:Т.к.
- 10. ПримерРешение:Синус и косинус.Вычислить синус и косинус t
- 11. Решить уравнение a) sin(t)= ,
- 12. ПримерРешить уравнение а)cos(t)=1/2 б) cos(t)>1/2 Синус и
- 13. ПримерРешение:Синус и косинус.Вычислить тангенс и котангенс t
- 14. Задачи для самостоятельного решения.1) Решить уравнение a)
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Синус и косинус.
Что будем повторять ,что будем изучать:
Определение синуса
и косинуса.
Определение тангенса и котангенса.
Основное тригонометрическое тождество
Формировать навыки решения простейших
уравнений и неравенств.Таблица значений синуса, косинуса, тангенса, котангенса.
Основные свойства.
Синус и косинус в жизни.
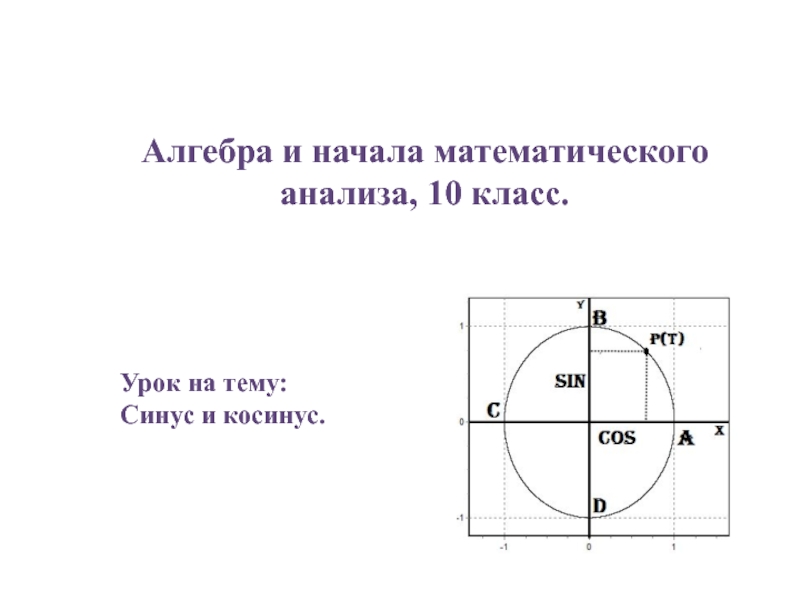
Слайд 3Определение.
Синус и косинус.
Ребята, давайте отметим на числовой окружности точку Р,
посмотрите рисунок,
наша точка Р соответствует некоторому числу t числовой окружности,
тогда абсциссу точки Р будем называть косинусом числа t и обозначать cos(t),
а ординату точки Р назовем синусом числа t и обозначим sin(t).
Наша точка Р(t) = Р(x,y) тогда:
X = cos(t)
Y = sin(t)
А как будет выглядеть запись синуса и косинуса на математическом языке?
Давайте посмотрим:
Слайд 4Тангенс и котангенс.
Отношение синуса числа t к косинусу того же числа называют тангенсом
числа t и обозначают tg(t).
Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и
обозначают ctg(t).Стоит заметить, так как на 0 делить нельзя, то, для
тангенса cos(t) ≠ 0, а для котангенса sin(t) ≠ 0
Определение.
Так же важно определить понятие тангенса и котангенса числа t числовой окружности, запишем определения:
Слайд 5Синус и косинус.
Основное тригонометрическое тождество.
Давайте вспомним уравнение числовой окружности:
нашему числу
Х соответствует абсцисса координатной плоскости, а числу Y – ордината,
посмотрим определение синуса и косинуса на первом слайде и получим:Важно, запомните!
Значения синуса, косинуса, тангенса, котангенса в четвертях окружности:
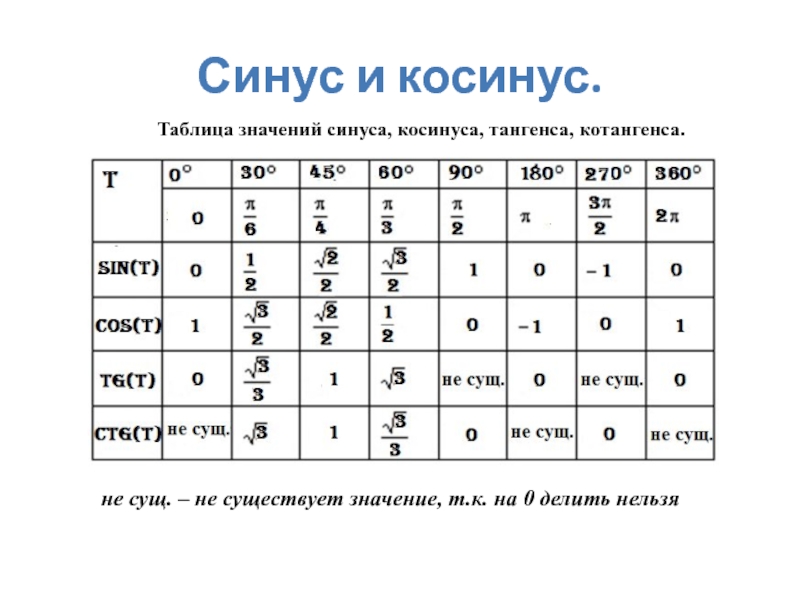
Слайд 6Таблица значений синуса, косинуса, тангенса, котангенса.
Синус и косинус.
не сущ. –
не существует значение, т.к. на 0 делить нельзя
Слайд 7Основные свойства.
Синус и косинус.
Для любого числа t справедливы равенства:
sin(-t) =
-sin(t)
cos(- t) = cos(t)
tg(- t) = -tg(t)
ctg(- t) =
-ctg(t) sin(t + 2π •k ) = sin(t)
cos(t +2π •k ) = cos(t)
sin(t + π ) = -sin(t)
cos(t +π ) = -cos(t)
tg(t + π •k ) = tg(t)
ctg(t +π •k ) = ctg(t)
sin(t + π/2 ) = cos(t)
cos(t +π/2 ) = -sin(t)
Слайд 8Синус и косинус.
Синус и косинус в жизни.
Для чего нужны синусы
и косинусы в обычной жизни?
На практике синусы и косинусы применяются
во всех инженерных специальностях, особенно в строительных. Их используют моряки и летчики в расчетах курса движения. Не обходятся без синусов и косинусов геодезисты, и даже путешественники. В географии применяют для измерения расстояний между объектами, а также в спутниковых навигационных системах.Слайд 9Пример
Вычислить синус и косинус t при: t=53π/4
Решение:
Т.к. числам t и
t+2π•k (k-целое число) соответствует одна и тоже точка числовой окружности:
53π/4
= (12 + 5/4) • π = 12π +5π/4 = 5π/4 + 2π•6Воспользуемся свойством sin(t + 2π •k ) = sin(t), cos(t +2π •k ) = cos(t)
sin(5π/4 + 2π•6 ) = sin(5π/4 ) = sin(π/4 + π)
cos(5π/4 + 2π•6 ) = cos(5π/4 )= cos(π/4 + π)
Воспользуемся свойством sin(t + π ) = -sin(t), cos(t +π) = -cos(t)
sin(π/4 + π )=-sin(π/4 )
cos(π/4 + π)=-cos(π/4 )
Из таблицы значений синуса и косинуса получаем:
sin(53π/4 ) =
Синус и косинус.
cos(53π/4 ) =
Слайд 10Пример
Решение:
Синус и косинус.
Вычислить синус и косинус t при: t= -49π/3
Т.к.
числам t и t+2π•k (k-целое число) соответствует одна и тоже
точка числовой окружности то:-49π/3 = -(16 + 1/3) • π = -16π +(-π/3) = (-π/3) + 2π•(-8)
Воспользуемся свойством sin(t + 2π •k ) = sin(t), cos(t +2π •k ) = cos(t)
sin(-π/3 + 2π•(-8) )=sin(-π/3 )
cos(-π/3 + 2π•(-8) )=cos(-π/3 )
Воспользуемся свойством sin(- t) = -sin(t), cos(- t) = cos(t)
sin(-π/3)=-sin(π/3 )
cos(-π/3)=cos(π/3 )
Из таблицы значений синуса и косинуса получаем:
sin(-49π/3 ) = -
cos(-49π/3)=
Слайд 11Решить уравнение a) sin(t)= , б)
sin(t) >
Пример
Синус и косинус.
Решение:
sin(t) – из определения, это ордината точки
числовой окружности. Значит на числовой окружности нужно найти точки с ординатой
и записать, каким числам t, они соответствуют - точки F и G на рисунке.
а) Точка F и G имееют координаты:
π/3 +2 π •k и 2π/3 +2 π •k
Ответ : a) t= π/3 +2 π •k и t= 2π/3 +2 π •k б) Уравнению y > ½ это дуга FG тогда:
б)π/3 +2 π •k
π/3 +2 π •k
Слайд 12Пример
Решить уравнение а)cos(t)=1/2 б) cos(t)>1/2
Синус и косинус.
cos(t) – из
определения, это абсцисса точки числовой окружности.
Значит на числовой окружности
нужно найти точки с абсциссой равной 1/2 и записать, каким числам t, они соответствуют – точки F и G на рисунке
а) Точка F и G соответствуют координаты:
-π/3 +2 π •k и π/3 +2 π •k
Ответ : а) t= -π/3 +2 π •k и t=π/3 +2 π •k б) Уравнению x >1/2
б) –π/3 +2 π •k
соответствует дуга FG тогда:
-π/3 +2 π •k
Слайд 13Пример
Решение:
Синус и косинус.
Вычислить тангенс и котангенс t при: t= -7π/3
Т.к.
числам t и t+2π•k (k-целое число) соответствует одна и тоже
точка числовой окружности то:-7π/3 = -(2 + 1/3) • π = -2π +(-π/3) = (-π/3) + 2π
Воспользуемся свойством tg(x+ π •k ) = tg(x), ctg(x+π •k ) = ctg(x)
tg((-π/3) + 2π ) = tg(- π/3)
сtg((-π/3) + 2π ) = сtg(- π/3)
Воспользуемся свойством tg(-x) = -tg(x), ctg(-x) = -ctg(x)
tg(-π/3)=-tg(π/3 )
сtg(-π/3)=-сtg(π/3 )
Из таблицы значений получаем:
tg(-7π/3) = -tg(π/3 ) =
сtg(-7π/3) = -сtg(π/3 ) = -
Слайд 14Задачи для самостоятельного решения.
1) Решить уравнение a) sin(t)= -½, б)
sin(t) > -½ в) sin(t) < -½
2) Решить уравнение а)
cos(t) = -½, б) cos(t) > -½, в) cos(t) < ½, Синус и косинус.