Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок алгебры в 9 классе "Квадратичная функция"
Содержание
- 1. Урок алгебры в 9 классе "Квадратичная функция"
- 2. Предмет математики столь серьезен, что не следует упускать ни одной возможности, сделать его более занимательным»(Б. Паскаль)
- 3. Тема урока: «Квадратичная функция и ее свойства»
- 4. График квадратичной функции - парабола
- 5. Древнегреческий математик и астроном Аполлоний Пергский (ок.
- 6. В Ергаках, существует удивительная скала, своей необычной
- 7. Два брата как бы взялись за руки,
- 8. Парабола в жизни
- 9. Слайд 9
- 10. Слайд 10
- 11. Полет снаряда Действительно, в абсолютном вакууме
- 12. Слайд 12
- 13. Первым, кто доказал, что
- 14. Представим себе, что очень узкая зеркальная полоска,
- 15. Вращая параболу вокруг ее оси, мы получим
- 16. Вот несколько примеров использования параболоидов:ПрожекторОтражательный телескоп - рефлектор Антенна представляет собой часть параболоида вращения
- 17. Если для решения той или иной практической
- 18. ПовторениеЛинейные функции.y = ах + bВерно!
- 19. ПовторениеФункции прямой пропорциональности.у = kxПравильно!
- 20. ПовторениеФункции обратной пропорциональности.у = k/xИ все!
- 21. Повторение.Квадратичные функции.Молодцы!у = ах2 + bx +c
- 22. у = а y = kxy =
- 23. Найдите соответствия:Хорошо!
- 24. Не строя график функции у = х2
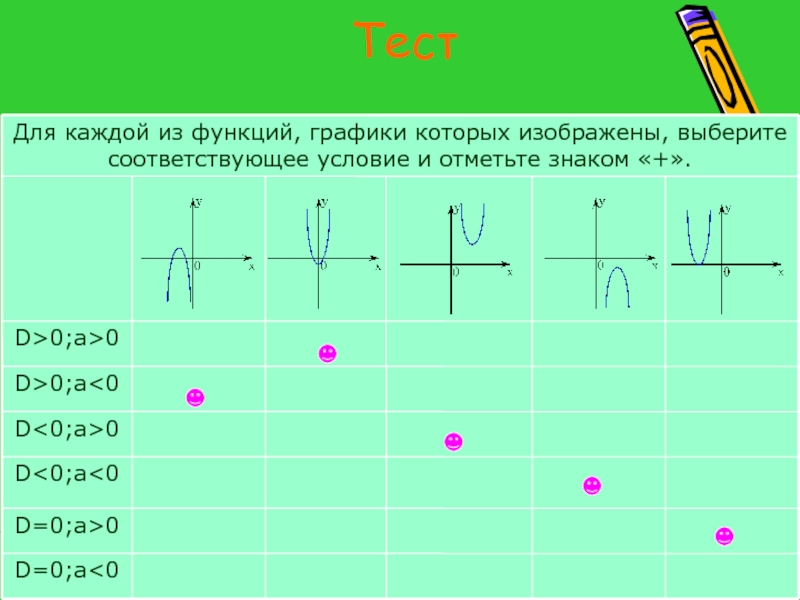
- 25. Тест
- 26. Тест.
- 27. Построение графика функции у = ах2 + bх +с.1.Определить направление ветвей параболы.Парабола.
- 28. Построение графика функции у = ах2 +
- 29. у = 2х2 + 8х - 1
- 30. Построение графика функции у = ах2 +
- 31. Построение графика функции у = ах2 +
- 32. у = х2 - 2х - 3Построить график функцииапрап
- 33. 1. а=1>0, ветви вверх2. КВП: у =
- 34. 5. Таблица у = х2 - 2х - 3
- 35. Слайд 35
- 36. Домашнее задание:Стр. 115№ 176(1)№178(1)Начертить и исследовать
- 37. 1.гКаков вид графика функцииобратной пропорциональности? иепалобр
- 38. 1.2.ргиепалобрКаков вид графика квадратичной функции?пабалоа
- 39. 1.2.3.иргиепалобр3. Как называется координата точки по оси Ох?пабалоабасцсас
- 40. 1.2.3.4.иаргиепалобр4. Как называется координата точки по оси Оу?пабалоабасцсасронидат
- 41. 1.2.3.4.5.ифаргиепалобр5. Один из способов задания функции. пабалоабасцсасронидатроалум
- 42. 1.2.3.4.5.6.ифаргиепалобр6. Переменная величина,значение которой зависитот изменения другойвеличины.пабалоабасцсасронидатроалумфуикнця
- 43. Слайд 43
- 44. РефлексияПонравился ли тебе урок?За что ты можешь похвалить себя?Какую отметку за работу ты себе поставишь?
- 45. Получай!!!5
- 46. Используемая литератураАлгебра 9 класс, авт. Макарычев Ю.Н.,Миндюк
- 47. Скачать презентанцию
Предмет математики столь серьезен, что не следует упускать ни одной возможности, сделать его более занимательным»(Б. Паскаль)
Слайды и текст этой презентации
Слайд 1Квадратичная функция
урок алгебры в 9классе
Автор Калинина Т Н
учитель математики
МОУ Некрасовская
СОШ
Слайд 2
Предмет математики столь серьезен, что не следует упускать ни одной
возможности, сделать его более занимательным»
(Б. Паскаль)
Слайд 5Древнегреческий математик и астроном Аполлоний Пергский (ок. 260 - 170
гг. до н.э.) дал этой кривой название парабола [от греч.
para - рядом, около и ballein - бросать, метать]
Слайд 6
В Ергаках, существует удивительная скала, своей необычной формой она напоминает
параболу. Ее вертикальные стенки, разрисованные полосами временных водотоков, имеют высоту
около 500 метров. Скала называется Братья.
Слайд 7Два брата как бы взялись за руки, образовав идеально ровную
покатую поверхность параболы: массивный Старший Брат и более тонкий Младший,
слегка наклонившийся к нему своим острым, как лезвие, гребнем. В долине, со стороны Младшего Брата, расположилось изумрудное горное озеро - озеро Горных Духов. Согласно древней легенде, эти самые духи и заколдовали двух Братьев, оставив их здесь охранять сказочные сокровища.
Слайд 11
Полет снаряда
Действительно, в абсолютном вакууме снаряд летел бы
по правильной Но в атмосфере с высотой сопротивление воздуха уменьшается,
и, кроме того, чтобы точно рассчитать траекторию, необходимо учитывать скорость ветра и ряд других факторов. Поэтому важность этой науки очевидна, особенно в век баллистических ракет и компьютеров.параболе
Слайд 13
Первым, кто доказал,
что пушечное ядро летит
по параболической кривой,
был Галилео Галилей.
Каждая планета солнечной системы вращается по
параболе
Слайд 14
Представим себе, что очень узкая зеркальная полоска, изогнута в форме
дуги параболы. Если мы параллельно оси параболы направим пучок лучей,
то они, отразившись от зеркала соберутся в некоторой точке F, расположенной на оси и называемой фокусом параболыИ обратно, если мы поместим источник света в фокусе параболы, то всякий его луч, отраженный от зеркала направится параллельно оси параболы.
(фокус –очаг,
в переводе
с латинского)
Слайд 15
Вращая параболу вокруг ее оси, мы получим поверхность, называемую параболоидом
вращения. Параболические зеркала и другие аналогичные им приспособления, использующие описанное
свойство параболы, изготовляются в форме параболоида.
Слайд 16Вот несколько примеров использования параболоидов:
Прожектор
Отражательный телескоп - рефлектор
Антенна представляет собой
часть параболоида вращения
Слайд 17Если для решения той или иной практической задачи требуется направить
или принять параллельный пучок радиоволн, то используют параболические антенны, основанные
на том же принципе, что и параболические зеркала.РТ-70 в Евпатории
РТ-70 в Голдстоуне
РТ-64 в Калязине
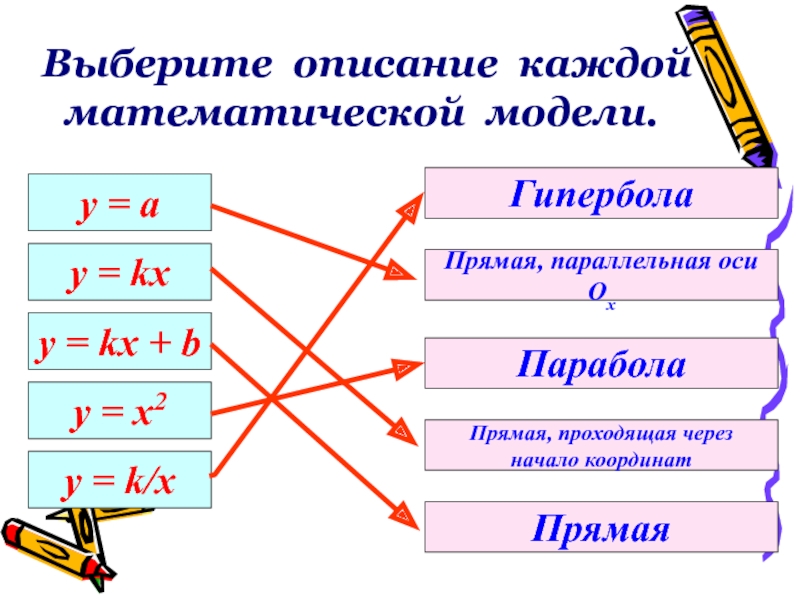
Слайд 22у = а
y = kx
y = kx + b
y
= x2
y = k/x
Прямая, параллельная оси Ох
Парабола
Гипербола
Прямая, проходящая через
начало
координатПрямая
Выберите описание каждой
математической модели.
Слайд 27Построение графика функции у = ах2 + bх +с.
1.
Определить направление
ветвей параболы.
Парабола.
Слайд 28Построение графика функции у = ах2 + bх +с.
2.
Найти координаты
вершины параболы
(т; п).
3.
Провести ось
симметрии.
О (т;п)
Слайд 30Построение графика функции у = ах2 + bх +с.
4.
Определить точки
пересечения графика
функции с осью Ох, т.е. найти нули
функции.
(х1;0)
(х2;0)
Слайд 31Построение графика функции у = ах2 + bх +с.
5.
Составить таблицу
значений функции
с учетом оси симметрии параболы.
Слайд 331. а=1>0, ветви вверх
2. КВП:
у = х2 - 2х
- 3
3. Ось симметрии х=1
(1; -4)
4*. Пересечение
с с ОХ: у=0
0, ветви вверх2. КВП: у = х2 - 2х -" alt="1. а=1>0, ветви вверх2. КВП: у = х2 - 2х - 3 3. Ось симметрии х=1">
Слайд 421.
2.
3.
4.
5.
6.
и
ф
а
р
г
и
е
п
а
л
о
б
р
6. Переменная величина,
значение которой зависит
от изменения другой
величины.
п
а
б
а
л
о
а
б
а
с
ц
с
а
с
р
о
н
и
д
а
т
р
о
а
л
у
м
ф
у
и
к
н
ц
я
Слайд 44Рефлексия
Понравился ли тебе урок?
За что ты можешь похвалить себя?
Какую отметку
за работу ты себе поставишь?
Слайд 46Используемая литература
Алгебра 9 класс, авт. Макарычев Ю.Н.,Миндюк Н.Г. и др
ГИА
Алгебра Типовые тестовые задания.9класс авт. Мирошин В.В
Интернет ресурсы
