Эконометрика: история развития, определение, особенности метода, базовые понятия

экономических явлений и их взаимосвязей или • совокупность методов

анализа связей между различными экономическими показателями (факторами) на основании реальных статистических данных с использованием аппарата теории вероятностей и математической статистики

Предмет эконометрики –
• количественные взаимосвязи между экономическими переменными
или
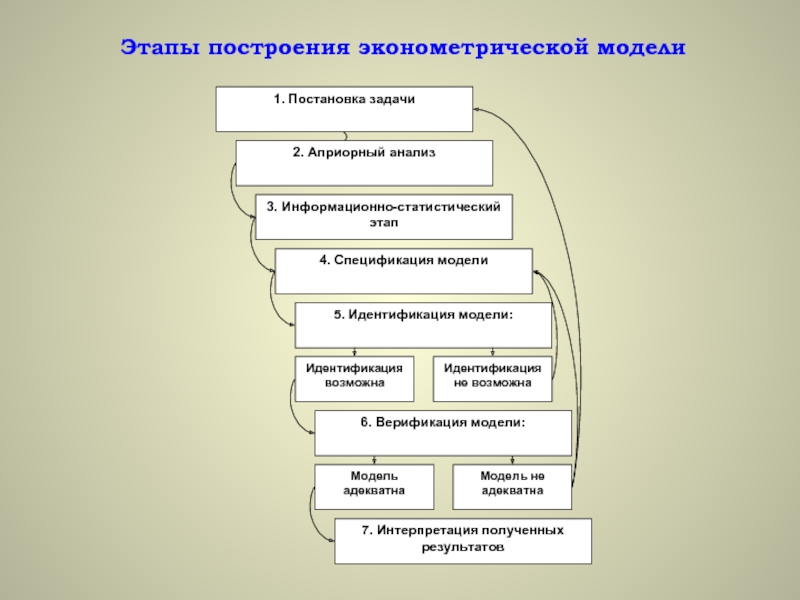
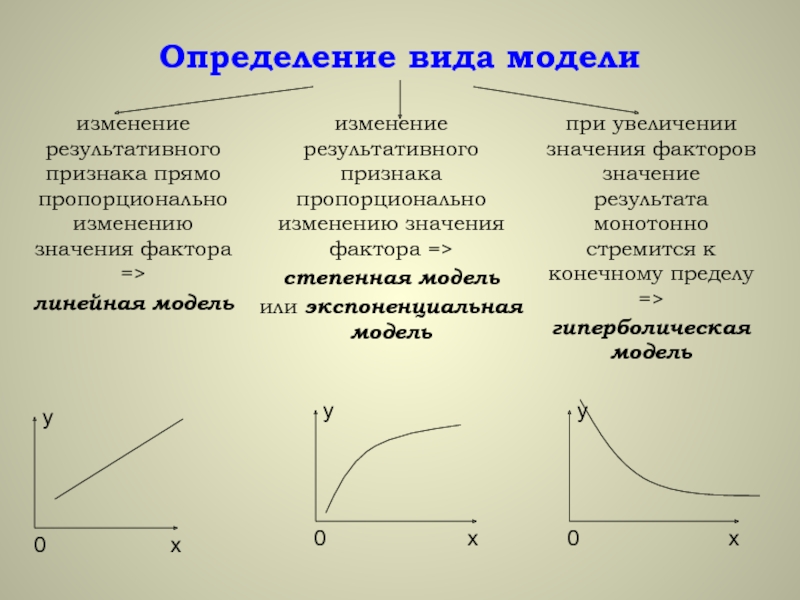
• построение функциональных зависимостей между переменными, называемых эконометрическими моделями

явлениями, при которой изменение одного из них, называемого причиной, ведет

к изменению другого, называемого следствием. Особенности: 1) Х—>Х’—>Х’’—>Y, где Х - причина (фактор; экзогенная, независимая, объясняющая, входная переменная) Y- следствие (результат; эндогенная, зависимая, объясняемая, выходная переменная) Х’ и Х’’ - промежуточные факторы 2) одновременное воздействие большого количества факторов

Характеристика взаимосвязей в модели:
по направлению изменения связи: 1) прямая
2) обратная
по аналитическому выражению: 1) линейная
2) нелинейная
по характеру проявления: 1) функциональная (детерминированная)
2) стохастическая

- результативный признак;
f(α, x) - функционал,

выражающий вид и структуру взаимосвязей;
x = (x1, x2,…, xn) - вектор значений факторов xi;
α = (α0, α1, α2,…, αn) - вектор некоторых произвольных констант, называемых параметрами модели;
ε - ошибка модели, или возмущение.

другие

это означает, что с ростом цены на 1 д. е.

спрос в среднем уменьшается на 2 д. е.

# Например: если зависимость цены у от спроса х характеризуется уравнением:

это означает, что с ростом спроса на 1% цена в среднем увеличивается на 3,8%.

связи (с помощью расчета коэффициентов корреляции) между переменными без их

разделения на факторные и результативные.

Регрессионный анализ – это раздел математической статистики, изучающий форму зависимости между факторными и результативными переменными.

Построение уравнения регрессии

зависимости):




где rxy – линейный коэффициент парной корреляции;

- средние квадратические отклонения переменных х и у (обобщающая характеристика размеров вариации признака в совокупности);
сov(x,y) – ковариация признаков (мера линейной зависимости двух 
случайных величин).

– 1 ≤ rxy ≤ 1
rxy > 0 – связь прямая
rxy < 0 – связь обратная
(|0-0,3| – практически отсутствует; |0,3-0,5| – слабая;
|0,5-0,7| – умеренная; |0,7-0,9|– сильная )
|rxy| = 1 – связь функциональная
rxy = 0 – связь отсутствует

вариацией фактора ):


















где R – коэффициент детерминации

(чем ближе к 1, тем в большей степени уравнение пригодно для прогнозирования);
Dост, D(y) – дисперсия остаточная (необъясненная) и общая дисперсия результативного признака.

0 ≤ R ≤ 1
R = 1 – связь функциональная

расчетных значений от фактических (допустимый предел – не более 15%).