Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аксиомы. Как устроена теорема. Свойства и признаки.
Содержание
- 1. Аксиомы. Как устроена теорема. Свойства и признаки.
- 2. Аксиомы геометрииЧерез любые две точки можно провести
- 3. Аксиома – греческое слово, означает «достоинство», «уважение»,
- 4. Теорема – греческое слово, означает «зрелище»,
- 5. Устройство теоремыЕсли «УСЛОВИЕ», то «ЗАКЛЮЧЕНИЕ».
- 6. Теорема о равенстве треугольниковУсловие (дано): две
- 7. Условие (дано): вертикальные углы.Заключение (доказать): эти углы равны.Если углы вертикальные, то они равны.
- 8. Если углы смежные, то их сумма 180°Условие (дано): смежные углы.Заключение (доказать): их сумма равна 180°.
- 9. Свойства хорошей погодыЕсли погода хорошая, то поют
- 10. Признаки хорошей погодыЕсли светит солнце, то погода
- 11. Cвойства Если
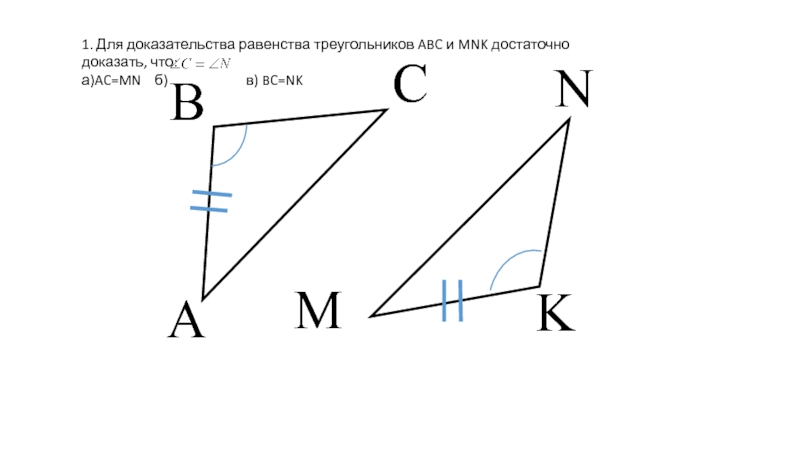
- 12. Первый признак равенства треугольниковЕсли две стороны и
- 13. Скачать презентанцию
Аксиомы геометрииЧерез любые две точки можно провести прямую и при том только одну.Из трех точек на прямой одна и только одна лежит между двумя другими.На любом луче от его начала можно
Слайды и текст этой презентации
Слайд 2Аксиомы геометрии
Через любые две точки можно провести прямую и при
том только одну.
Из трех точек на прямой одна и только
одна лежит между двумя другими.На любом луче от его начала можно отложить отрезок, равный данному и при том только один.
От любого луча в заданную сторону можно отложить угол, равный данному и при том только один.
Слайд 3Аксиома – греческое слово, означает «достоинство», «уважение», «авторитет». Первоначально имело смысл «самоочевидная
истина». Термин впервые встречается у Аристотеля и перешел в математику от философов
Древней Греции.
Слайд 4Теорема – греческое слово, означает «зрелище», «представление». В математике греков
это слово стало употребляться в смысле «истина, доступная созерцанию». Само
греческое слово происходит от слова «рассматриваю», «обдумываю». Слово, как математический термин, встречается у Аристотеля.
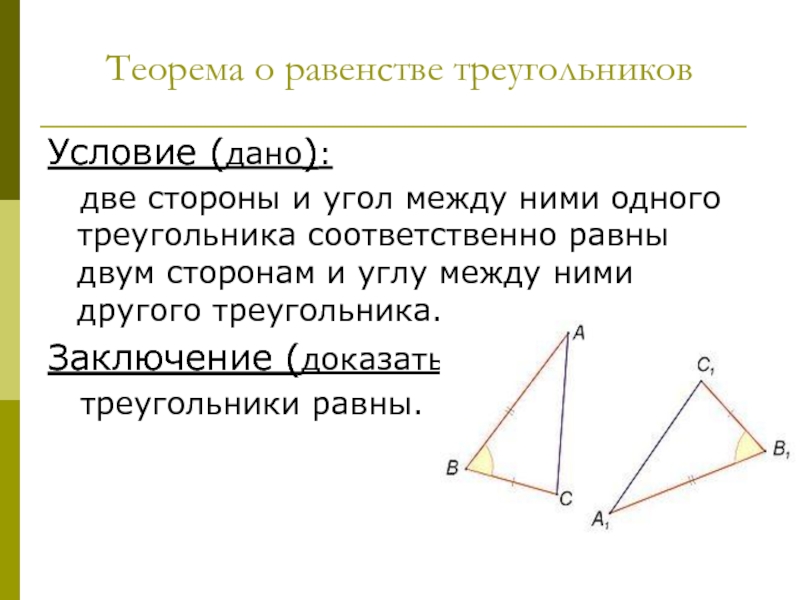
Слайд 6Теорема о равенстве треугольников
Условие (дано):
две стороны и
угол между ними одного треугольника соответственно равны двум сторонам и
углу между ними другого треугольника.Заключение (доказать):
треугольники равны.
Слайд 7
Условие (дано): вертикальные углы.
Заключение (доказать): эти углы равны.
Если углы
вертикальные, то они равны.
Слайд 8Если углы смежные, то их сумма 180°
Условие (дано): смежные углы.
Заключение
(доказать): их сумма равна 180°.
Слайд 9Свойства хорошей погоды
Если погода хорошая, то поют птицы.
Если погода хорошая,
то веселое настроение.
Если погода хорошая, то можно гулять.
Слайд 10Признаки хорошей погоды
Если светит солнце, то погода хорошая
Если нет ветра
и дождя, то погода хорошая.
Если тепло и ясно, то погода
хорошая.Слайд 12Первый признак равенства треугольников
Если две стороны и угол между ними
одного
треугольника соответственно
равны двум сторонам и углу между
ними другого
треугольника , то такие треугольники равны.