Четырехугольники 8 калсс

1. Что такое четырехугольник?
2. Назвать виды четырехугольников, какие мы выучили.
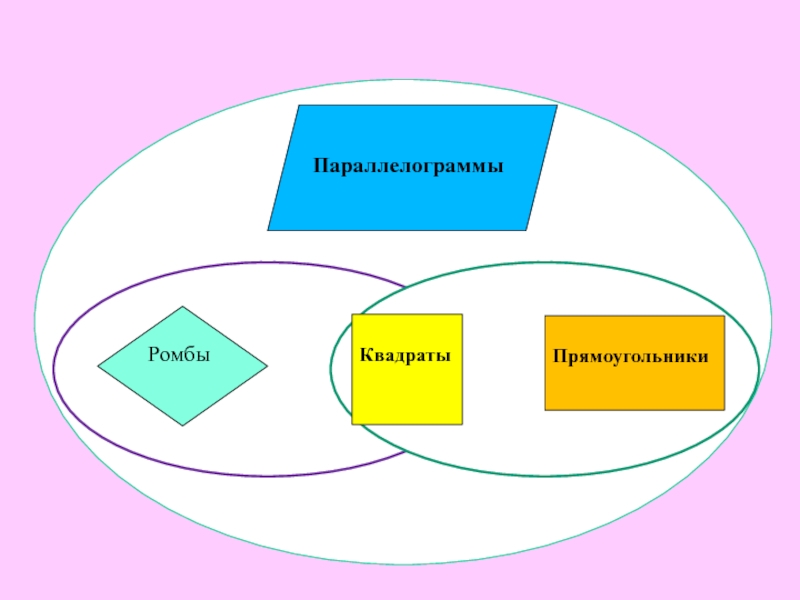
3. Дать определение параллелограмма и сформулировать его свойства.
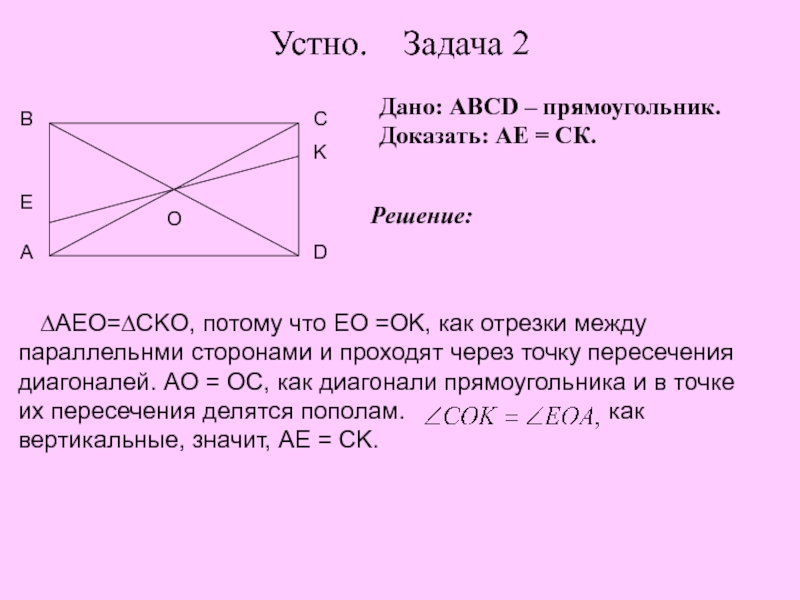
4. Дать определение прямоугольника и сформулировать его свойства.
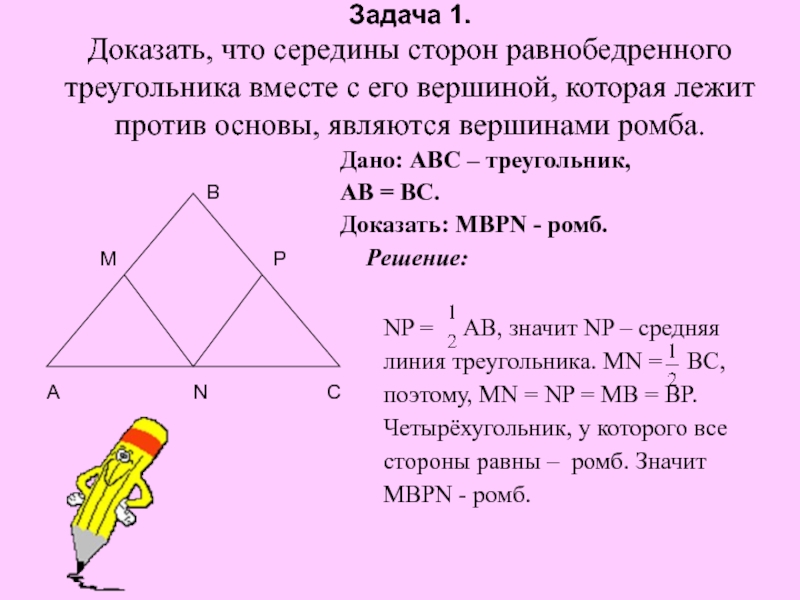
5. Дать определение ромба и сформулировать его свойства.
6. Определение и свойства квадрата.
7. Квадрат имеет свойства прямоугольника и ромба.
8. Какой четырехугольник называется трапецией?
9. Сформулировать теорему о средней линии трапеции.
10. Сформулировать теорему Фалеса .

и параллельны, то он является параллелограммом.
2. Если противоположные стороны четырехугольника

попарно равны, то этот четырехугольник параллелограмм.
3. Четырехугольник, у которого все стороны равны, является ромбом.
4. Если у параллелограмма диагонали равны, то он является прямоугольником.

то он является ромбом.
6. Параллелограмм, у которого все углы прямые,

называется прямоугольником.
7. Середины сторон четырехугольника являются вершинами параллелограмма.
8. В равнобедренной трапеции углы при основании равны и диагонали равны.
9. Сумма противоположных углов вписанного четырехугольника равна 180°.
10. Сумма противоположных сторон описанного четырехугольника равны.

то он не может быть прямоугольником.

2. Каждый квадрат является прямоугольником.
3. Существует ли ромб, который является прямоугольником.
4. Какой прямоугольник не является ромбом.

5. Существует квадрат, который не является ромбом.

(Да)

(Да)

(Квадрат)

(Нет)

(Квадрат)

ромба.
2. Почему теорему о средней линии трапеции можно перенести

на произвольный параллелограмм?
3. Существует ли трапеция, у которой два противоположных угла острые? У которой два противоположных угла прямые?
4. Можно ли построить трапецию с тремя прямыми углами?

AM – биссектриса А,

BN – биссектриса В.
Доказать: BN AM.

Доказательство

А + В = 180º, как сумма внутренних односторонних углов при параллельных прямых ВС и АD и секущей АВ. Поскольку АМ и BN – биссектрисы, ОВА + ВАО = 90º. Тогда AOB = 90º.

СК.


∆AEO=∆CKO, потому что EO =OK, как отрезки

между параллельнми сторонами и проходят через точку пересечения диагоналей. AO = OC, как диагонали прямоугольника и в точке их пересечения делятся пополам. как вертикальные, значит, AE = CK.

Решение:

АВ=DС.
ODA = OAD , потому что DО =

ОА. DAC = BCA, как внутренние разносторонние при DА // CB и секущей СА. BDA = DBC, как внутренние разносторонние при DA // CB и секущей DB. CO = OB, так как в треугольнике углы при основании равны.
Поэтому, в треугольниках DOC и AOB: DO = OA; CO = OB; DOC = AOB, как вертикальные. Значит, AB = DC.

Решение:

его вершиной, которая лежит против основы, являются вершинами ромба.

NP =

AB, значит NP – средняя линия треугольника. МN = BС, поэтому, МN = NP = МВ = ВР.
Четырёхугольник, у которого все стороны равны – ромб. Значит МВРN - ромб.

Дано: АВС – треугольник, АВ = ВС.
Доказать: МВРN - ромб.

Решение:

по трём сторонам.
Проведем

прямую и .
3) Доказано: и (как противоположные стороны параллелограмма). 4) Трапеция – построена.

120°. Вычислите угол между диагональю прямоугольника и меньшей стороной прямоугольника.
2

вариант В равнобедренной трапеции большое основание равняется 3,7дм, боковая сторона равняется 1,5дм, а угол между ними 60°. Вычислите среднюю линию трапеции.

Решение

. OAD = ODA, потому, чоти диагонали прямоугольника равны и в точке их пересечения делятся пополам. OAD = (180°–120°):2 = 30°. OAD = BCA, как внутренние разносторонние. OCD = 90°–30°= 60°.
 

Решение:

= 1,5дм.
Найти: MN.

Решение
AK – катет лежащий напротив угла 30°.
AK = AB = 0,75дм. AK = PD = 0,75дм, так как ∆АВК = ∆СРD по гипотенузе и острому углу. ВС = 3,7- 1,5 = 2,2 (дм).
MN = (дм).
 

 

А

B

C

K

M

N

D

P

таблице.