Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дополнительные построения в трапеции при решении задач 8 класс
Содержание
- 1. Дополнительные построения в трапеции при решении задач 8 класс
- 2. Основные подходы к решению задач о трапециях:Подобие
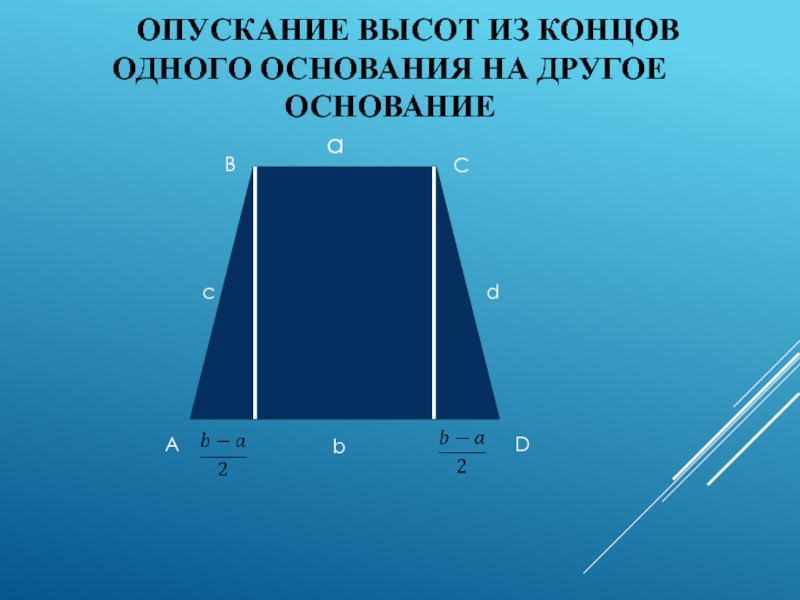
- 3. 1. Опускание высот из концов одного
- 4. Опускание высот из концов одного основания на другое основание ADBCacdb
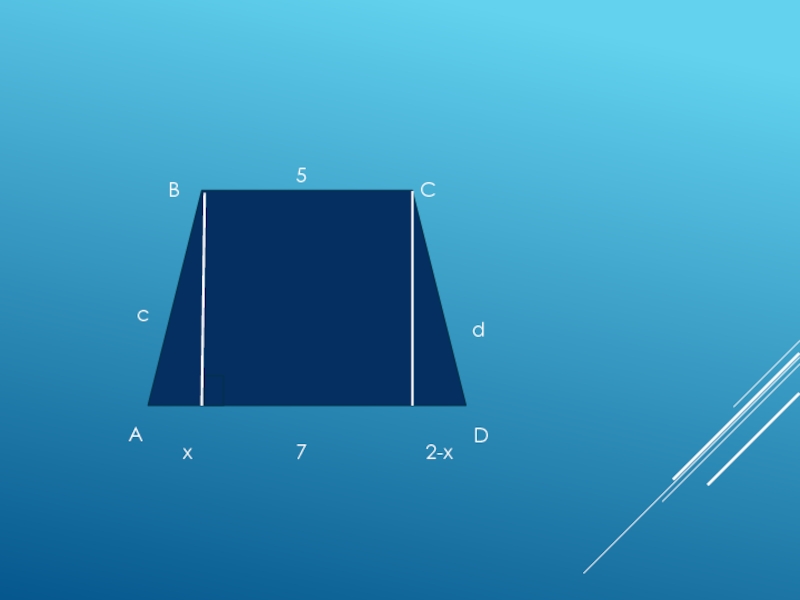
- 5. ADBCcd57x2-x
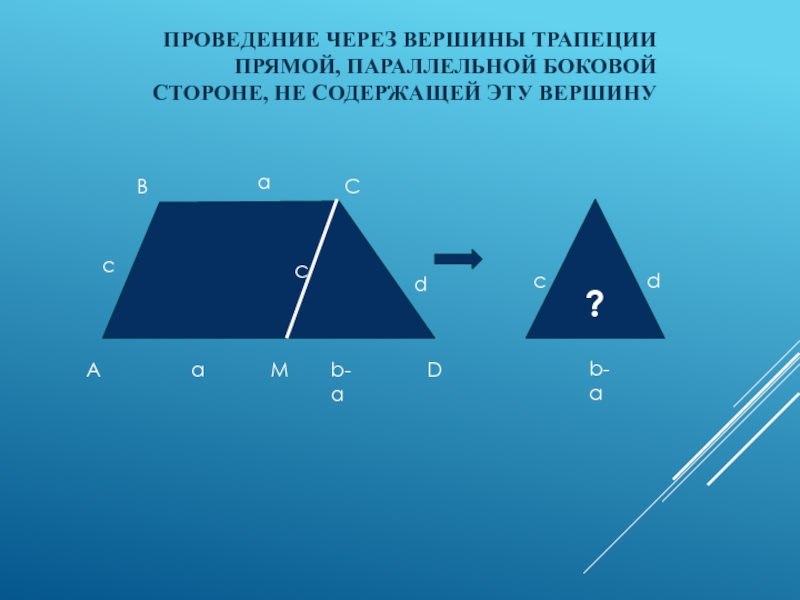
- 6. Проведение через вершины трапеции прямой, параллельной боковой
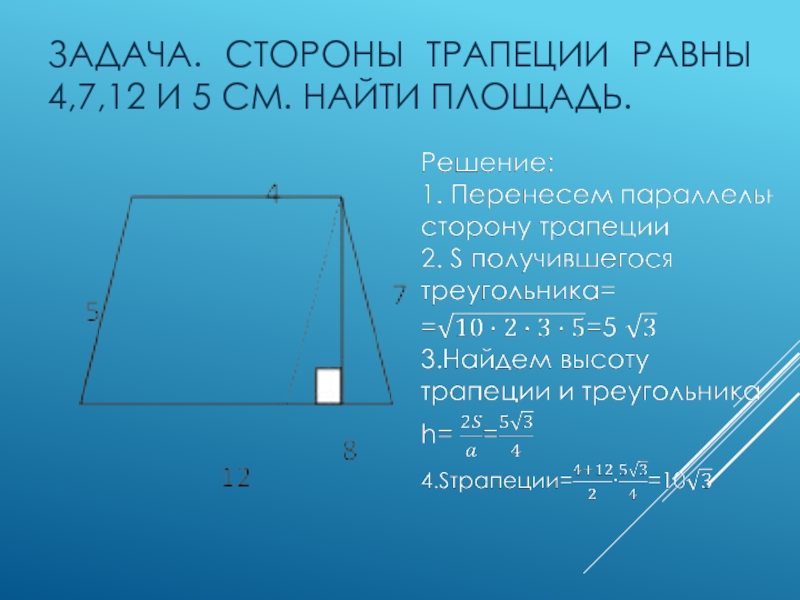
- 7. Задача. Стороны трапеции равны 4,7,12 и 5 см. Найти площадь.
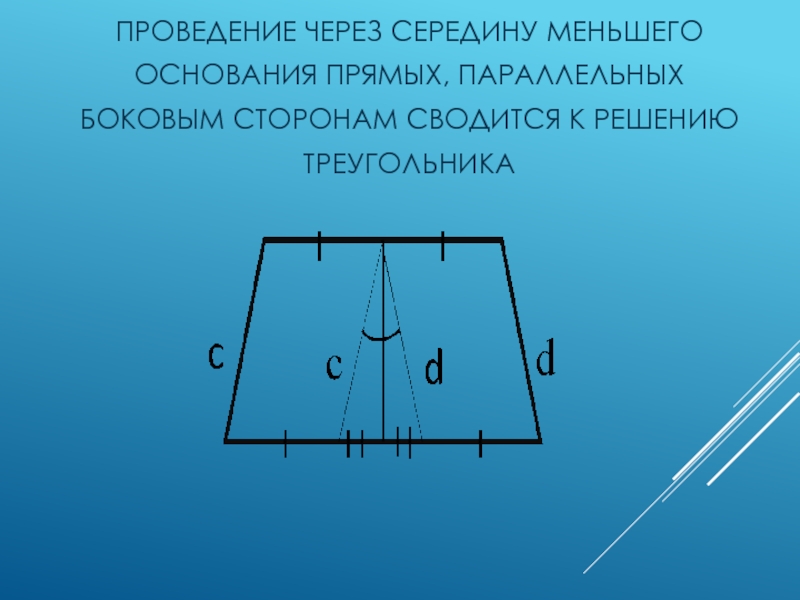
- 8. Проведение через середину меньшего основания прямых, параллельных боковым сторонам сводится к решению треугольника
- 9. Задача. В трапеции средняя линия равна 4
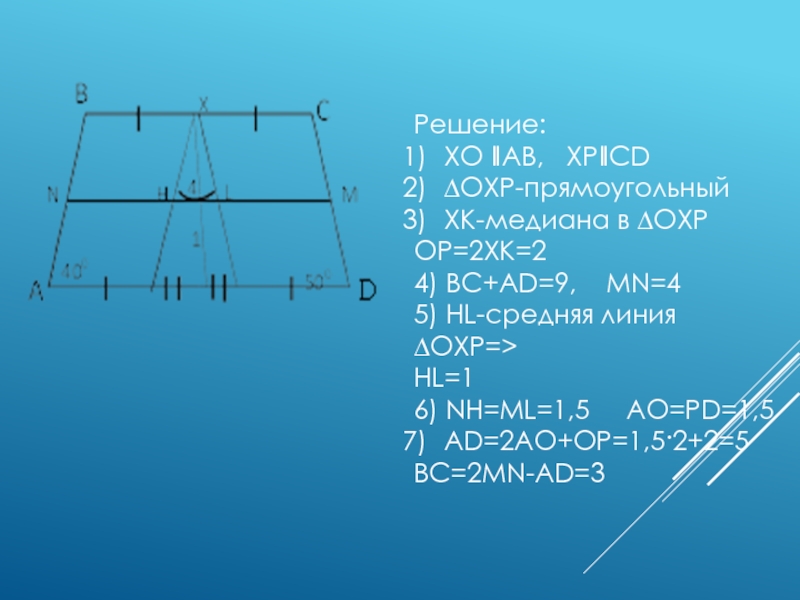
- 10. Решение:XO ‖AB, XP‖CD∆OXP-прямоугольныйXK-медиана в ∆OXPOP=2XK=24) BC+AD=9, MN=45) HL-средняя линия ∆OXP=>HL=16) NH=ML=1,5 AO=PD=1,5AD=2AO+OP=1,5·2+2=5BC=2MN-AD=3
- 11. Проведение через середину меньшего основания прямых, параллельных боковым сторонам
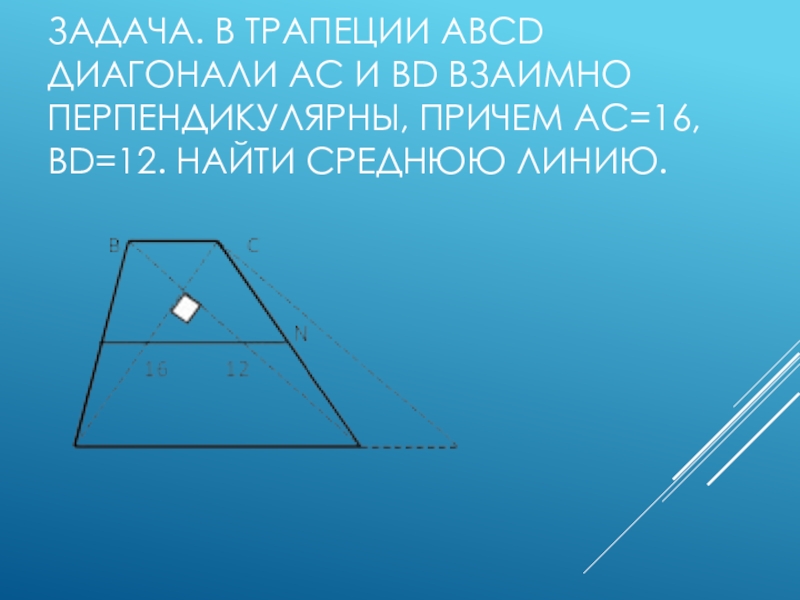
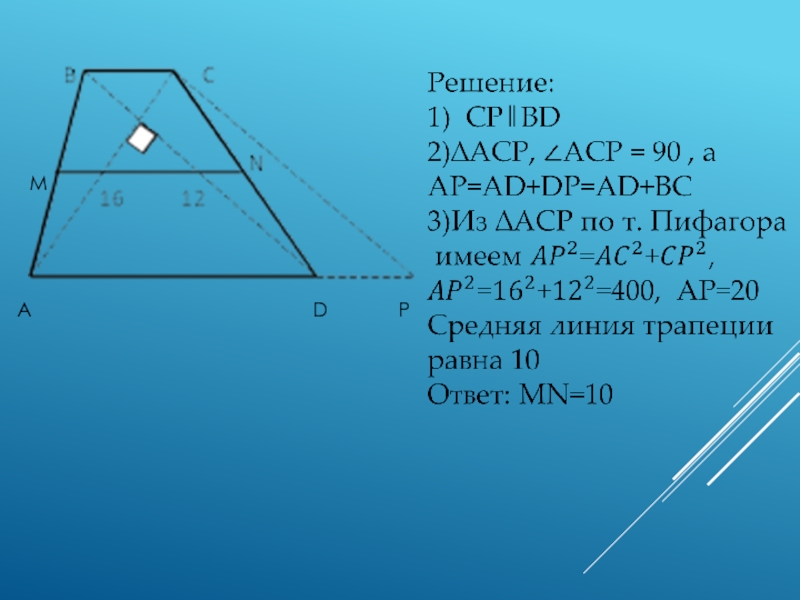
- 12. Задача. В трапеции ABCD диагонали AC и BD взаимно перпендикулярны, причем AC=16, BD=12. Найти среднюю линию.
- 13. MADP
- 14. Продолжение боковых сторон до пересечения
- 15. Слайд 15
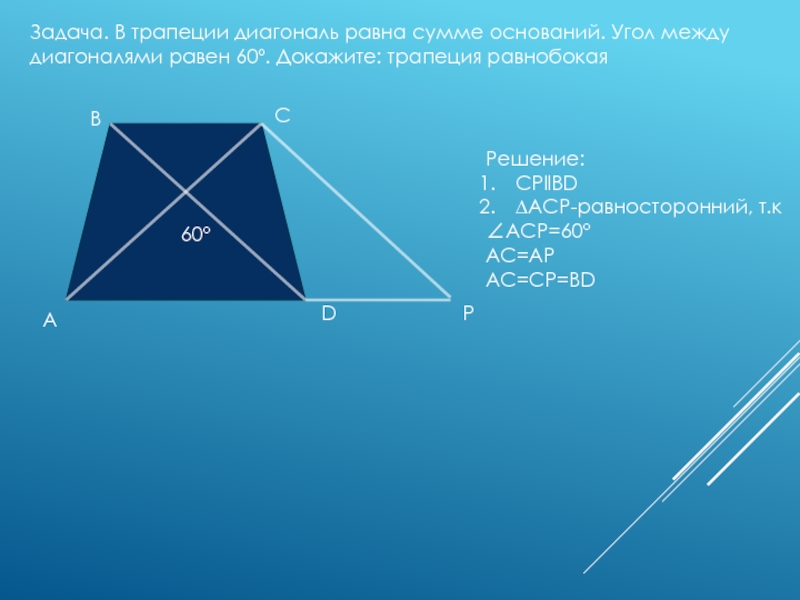
- 16. Задача. В трапеции диагональ равна сумме оснований. Угол между диагоналями равен 60º. Докажите: трапеция равнобокая60ºABCDPРешение:CPllBD∆ACP-равносторонний, т.к∠ACP=60ºAC=APAC=CP=BD
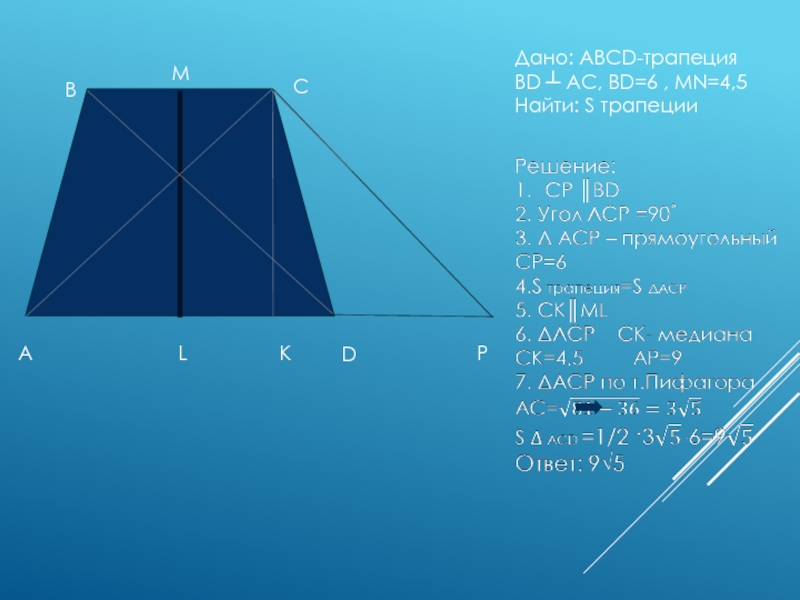
- 17. Дано: ABCD-трапецияBD ┴ AC, BD=6 , MN=4,5Найти: S трапецииABCDPKML
- 18. Вывод: Решение задач с помощью дополнительных построений
- 19. Слайд 19
- 20. Скачать презентанцию
Основные подходы к решению задач о трапециях:Подобие и пропорциональность Дополнительные построения Трапеция и площадь Трапеция и окружность
Слайды и текст этой презентации
Слайд 1
Дополнительные построения в трапеции при решении задач
Учитель математики высшей категории:
Ковалева Н.Ф.
Слайд 2Основные подходы к решению задач о трапециях:
Подобие и пропорциональность
Дополнительные
построения
Трапеция и площадь
Трапеция и окружность
Слайд 3 1. Опускание высот из концов одного основания на другое
основание
2. Проведение через вершины трапеции прямой, параллельной боковой стороне,
не содержащей эту вершину 3. Проведение через середину меньшего основания прямых, параллельных боковым сторонам
4. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину
5. Продолжение боковых сторон до пересечения
Слайд 6Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей
эту вершину
c
A
D
B
C
M
a
d
a
c
?
b-a
b-a
с
d
Слайд 8Проведение через середину меньшего основания прямых, параллельных боковым сторонам сводится
к решению треугольника
Слайд 9Задача. В трапеции средняя линия равна 4 см, углы при
одном из основании равны 40º и 50º. Найдите основания
трапеции, если отрезок, соединяющий середины оснований, равен 1 см.
Слайд 10Решение:
XO ‖AB, XP‖CD
∆OXP-прямоугольный
XK-медиана в ∆OXP
OP=2XK=2
4) BC+AD=9, MN=4
5) HL-средняя
линия ∆OXP=>
HL=1
6) NH=ML=1,5 AO=PD=1,5
AD=2AO+OP=1,5·2+2=5
BC=2MN-AD=3
Слайд 12Задача. В трапеции ABCD диагонали AC и BD взаимно перпендикулярны,
причем AC=16, BD=12. Найти среднюю линию.
Слайд 15
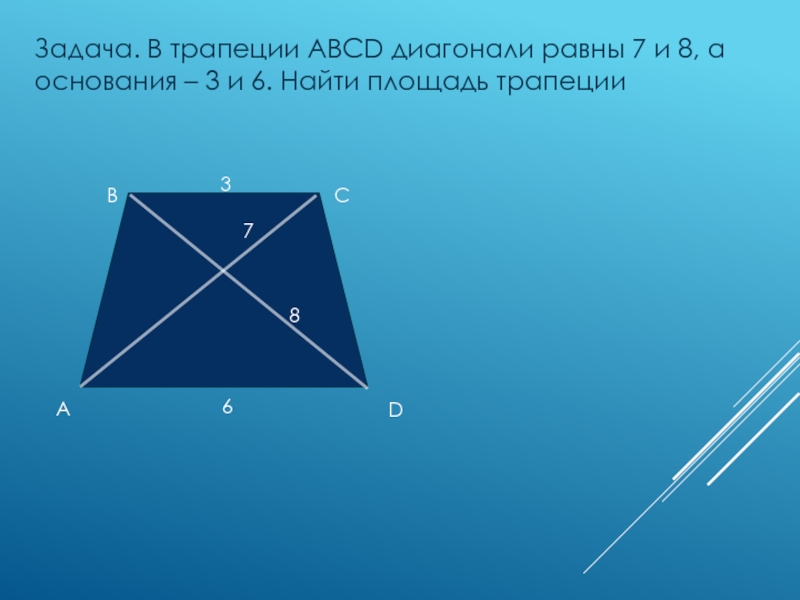
A
B
C
Задача.
В трапеции ABCD диагонали равны 7 и 8, а
основания
– 3 и 6. Найти площадь трапецииD
7
8
3
6
Слайд 16Задача. В трапеции диагональ равна сумме оснований. Угол между
диагоналями
равен 60º. Докажите: трапеция равнобокая
60º
A
B
C
D
P
Решение:
CPllBD
∆ACP-равносторонний, т.к
∠ACP=60º
AC=AP
AC=CP=BD
Слайд 18Вывод: Решение задач с помощью дополнительных построений не только быстрое
и проще, но и намного интересней, чем решение привычными способами
