Геометрические фигуры в пространстве

Содержание

1. Геометрические фигуры в пространстве
2. В стереометрии изучают фигуры в пространстве, называемые телами.
3. Поверхность многогранника состоит из конечного числа многоугольников,
4. Многогранник
5. Призма – это многогранник, у которого две
6. Призма прямая наклонная
7. Параллелепипед – призма, у которой основания параллелограммы.
8. Пирамида - это многогранник, одна грань которого
9. Многогранник, все грани которого правильные и равные
10. Тетраэдр - правильный четырехгранник. Он ограничен
11. Октаэдр - правильный восьмигранник. Он состоит
12. Икосаэдр -Икосаэдр - состоит из 20 равносторонних
13. Гексаэдр - правильный шестигранник. Это куб состоящий
14. Додекаэдр - правильный двенадцатигранник, состоит из двенадцати
15. Если соединить отрезками центры соседних граней правильного
16. Знаменитый математик Леонард Эйлер получил формулу: В
17. Тела вращения
18. Цилиндром называется тело, которое состоит из двух
19. Конусом называется тело, которое состоит из круга
20. Шаром называется тело, которое состоит из всех
21. Скачать презентанцию

В стереометрии изучают фигуры в пространстве, называемые телами.

Главная
Геометрия
Геометрические фигуры в пространстве

Слайды и текст этой презентации

Слайд 1Обирина Людмила Ивановна
Преподаватель КГБОУ СПО «НПК»
Геометрические фигуры в пространстве
Норильск, 2015

Слайд 2В стереометрии изучают фигуры в пространстве, называемые телами.

Слайд 3Поверхность многогранника состоит из конечного числа многоугольников, которые называются гранями

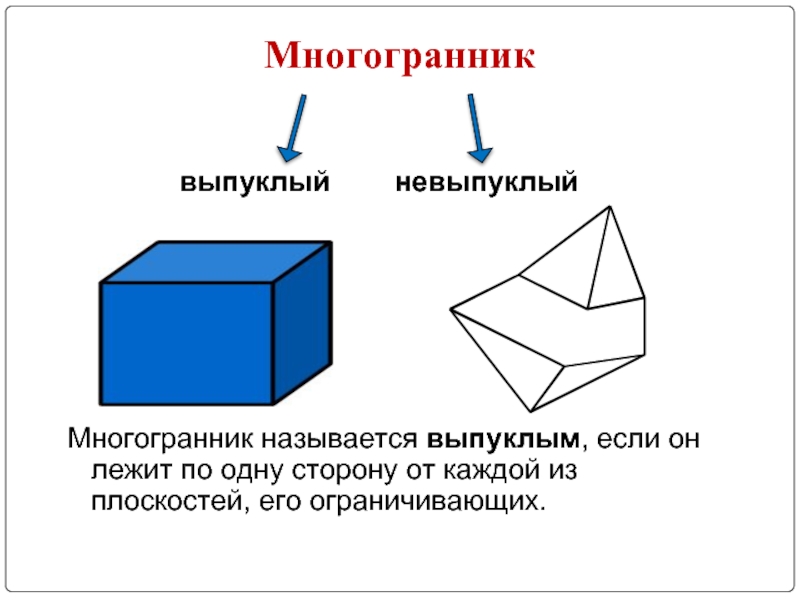
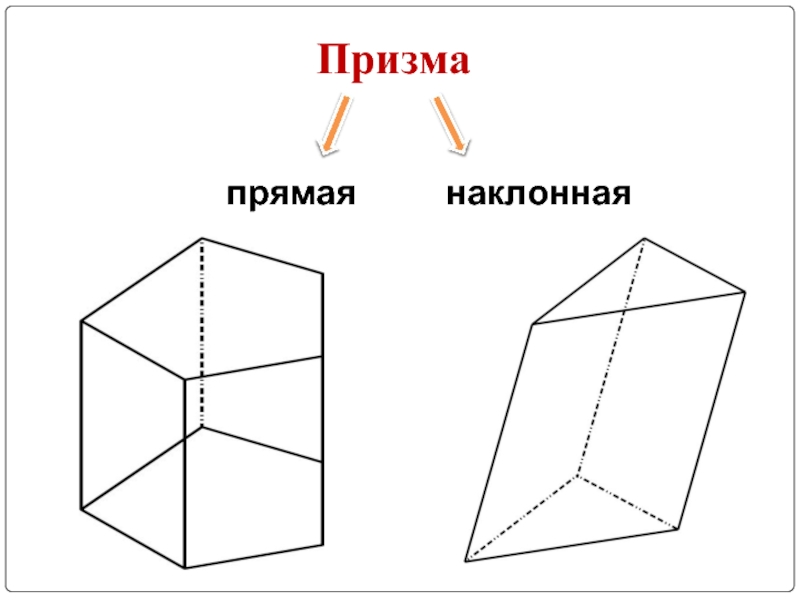
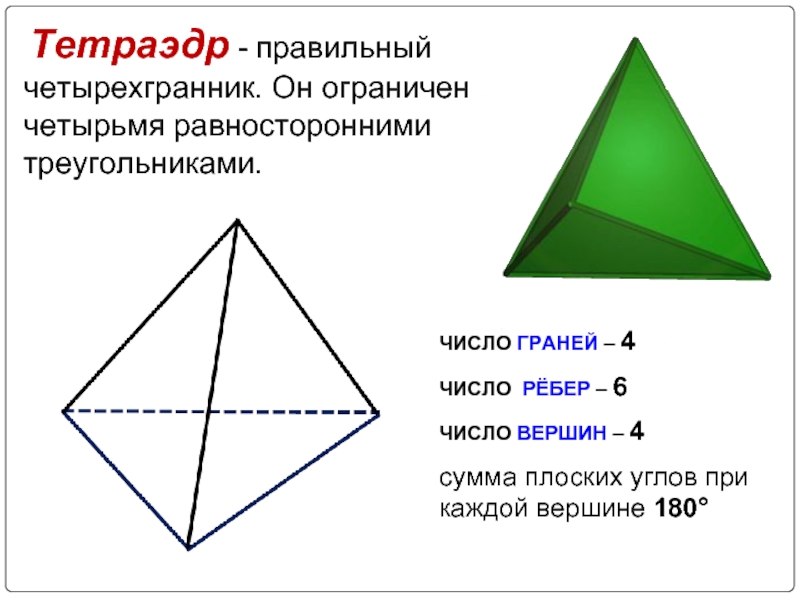
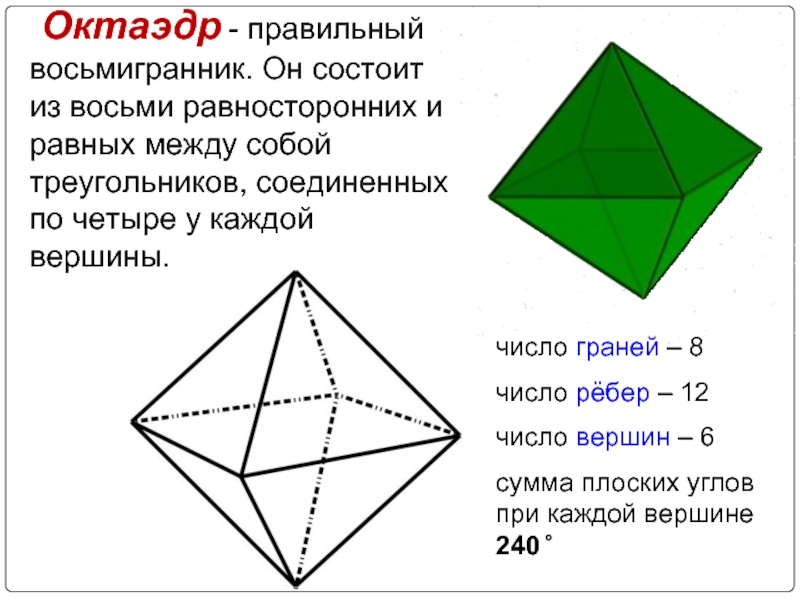
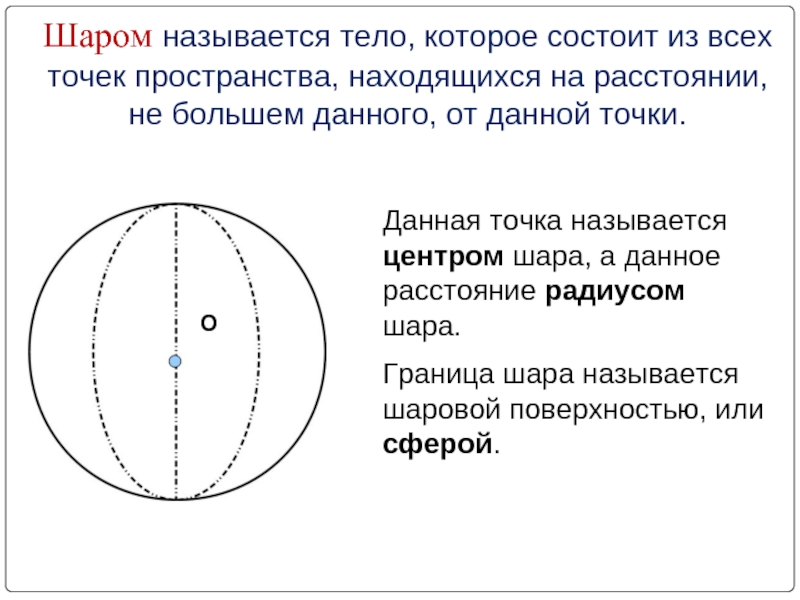
многогранника.
Стороны граней называются ребрами, а вершины - вершинами многогранника.

Отрезок, соединяющий две вершины, не лежащие в одной грани многогранника, называется его диагональю.

Многогранником называется тело, ограниченное конечным числом плоскостей.

Поверхность многогранника состоит из конечного числа многоугольников, которые называются гранями многогранника. Стороны граней называются ребрами, а вершины

Слайд 4Многогранник

выпуклый

невыпуклый

Многогранник называется выпуклым, если он лежит по одну сторону

от каждой из плоскостей, его ограничивающих.

Многогранник выпуклый невыпуклыйМногогранник называется выпуклым, если он лежит

Слайд 5Призма – это многогранник, у которого две грани (основания) лежат

в параллельных плоскостях, а все ребра вне этих граней параллельны

между собой.

Грани, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами.
Все боковые ребра равны и параллельны.
Все боковые грани призмы являются параллелограммами.
В основаниях призмы лежат равные многоугольники.

Призма – это многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне

Слайд 6Призма
прямая

наклонная

Слайд 7Параллелепипед – призма, у которой основания параллелограммы.
У параллелепипеда все

грани –параллелограммы.
У параллелепипеда противолежащие грани параллельны и равны.
Все диагонали

параллелепипеда пересекаются в одной точке.

Параллелепипед – призма, у которой основания параллелограммы. У параллелепипеда все грани –параллелограммы. У параллелепипеда противолежащие грани параллельны

Слайд 8Пирамида - это многогранник, одна грань которого многоугольник, а остальные

грани - треугольники с общей вершиной.
Грани, отличные от основания, называются

боковыми.
Общая вершина боковых граней называется вершиной пирамиды.
Ребра, соединяющие вершину пирамиды с вершинами основания называются боковыми.

Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной.Грани, отличные

Слайд 9Многогранник, все грани которого правильные и равные многоугольники, называется правильным.

Углы при вершинах правильного многогранника равны.

Тела Платона
Существует пять типов

правильных многогранников.
Впервые их описал древнегреческий философов Платон (IV в до н.э).

Многогранник, все грани которого правильные и равные многоугольники, называется правильным. Углы при вершинах правильного многогранника равны. Тела

Слайд 10 Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками.
ЧИСЛО

ГРАНЕЙ – 4
ЧИСЛО РЁБЕР – 6
ЧИСЛО ВЕРШИН – 4
сумма плоских

углов при каждой вершине 180°

Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками.ЧИСЛО ГРАНЕЙ – 4ЧИСЛО РЁБЕР – 6ЧИСЛО ВЕРШИН

Слайд 11 Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних

и равных между собой треугольников, соединенных по четыре у каждой

вершины.

число граней – 8
число рёбер – 12
число вершин – 6
сумма плоских углов при каждой вершине 240°

Октаэдр - правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по

Слайд 12Икосаэдр -
Икосаэдр - состоит из 20 равносторонних и равных треугольников,

соединенных по пять около каждой вершины.

число граней – 20
число рёбер

– 30
число вершин – 12
сумма плоских углов при каждой вершине 300°

Икосаэдр -Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.число граней

Слайд 13Гексаэдр - правильный шестигранник. Это куб состоящий из шести равных

квадратов, соединенных по три около каждой вершины.

число граней – 6
число

рёбер – 12
число вершин – 8
сумма плоских углов при каждой вершине 270°

Гексаэдр - правильный шестигранник. Это куб состоящий из шести равных квадратов, соединенных по три около каждой вершины.число

Слайд 14Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных

пятиугольников, соединенных по три около каждой вершины.

число граней – 12
число

рёбер – 30
число вершин – 20
сумма плоских углов при каждой вершине равна 324°

Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины.число

Слайд 15Если соединить отрезками центры соседних граней правильного многоугольника, то эти

отрезки станут ребрами другого правильного многогранника:
у куба – октаэдр,

у октаэдра – куб;
у икосаэдра – додекаэдр, у додекаэдра – икосаэдр;
у тетраэдра – снова тетраэдр.

Т.е. каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

Закон взаимности

Если соединить отрезками центры соседних граней правильного многоугольника, то эти отрезки станут ребрами другого правильного многогранника: у

Слайд 16Знаменитый математик Леонард Эйлер получил формулу:
В + Г -

Р = 2,
которая связывает
число вершин /В/, граней /Г/

и рёбер /Р/
любого многогранника.
Переменные в формуле не связаны ни с расстоянием, ни с углами.

Знаменитый математик Леонард Эйлер получил формулу: В + Г - Р = 2,которая связывает число вершин /В/,

Слайд 17Тела вращения

Слайд 18Цилиндром называется тело, которое состоит из двух кругов, не лежащих

в одной плоскости, и всех отрезков, соединяющих соответствующие точки этих

кругов.

Круги называются основаниями, а отрезки – образующими цилиндра.
Основания цилиндра равны.
Образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания.

Слайд 19Конусом называется тело, которое состоит из круга – основания конуса,

точки, не лежащей в плоскости этого круга, - вершины конуса

и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.

Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга,

Слайд 20Шаром называется тело, которое состоит из всех точек пространства, находящихся

на расстоянии, не большем данного, от данной точки.
Данная точка называется

центром шара, а данное расстояние радиусом шара.
Граница шара называется шаровой поверхностью, или сферой.

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной

Скачать презентацию

Разделы презентаций

Геометрические фигуры в пространстве

Содержание

Слайды и текст этой презентации

Слайд 1Обирина Людмила ИвановнаПреподаватель КГБОУ СПО «НПК»Геометрические фигуры в пространствеНорильск, 2015

Слайд 2В стереометрии изучают фигуры в пространстве, называемые телами.

Слайд 3Поверхность многогранника состоит из конечного числа многоугольников, которые называются гранями

многогранника. Стороны граней называются ребрами, а вершины - вершинами многогранника.

Слайд 4Многогранник выпуклый

невыпуклыйМногогранник называется выпуклым, если он лежит по одну сторону

Слайд 5Призма – это многогранник, у которого две грани (основания) лежат

в параллельных плоскостях, а все ребра вне этих граней параллельны

Слайд 6Призма прямая

наклонная

Слайд 7Параллелепипед – призма, у которой основания параллелограммы. У параллелепипеда все

грани –параллелограммы. У параллелепипеда противолежащие грани параллельны и равны.Все диагонали

Слайд 8Пирамида - это многогранник, одна грань которого многоугольник, а остальные

грани - треугольники с общей вершиной.Грани, отличные от основания, называются

Слайд 9Многогранник, все грани которого правильные и равные многоугольники, называется правильным.

Углы при вершинах правильного многогранника равны. Тела ПлатонаСуществует пять типов

Слайд 10 Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками.ЧИСЛО

ГРАНЕЙ – 4ЧИСЛО РЁБЕР – 6ЧИСЛО ВЕРШИН – 4сумма плоских