Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
7 класс, Геометрия Задачи по теме "Смежные и вертикальные углы"
Содержание
- 1. 7 класс, Геометрия Задачи по теме "Смежные и вертикальные углы"
- 2. 1265°?Задача – 1180°– 65°115°∠1 и ∠2 – смежные углы
- 3. 12130°?Задача – 2180°– 130°50°∠1 и ∠2 – смежные углы
- 4. 1273°?Задача – 373°∠1 и ∠2 – вертикальные углы∠1 =
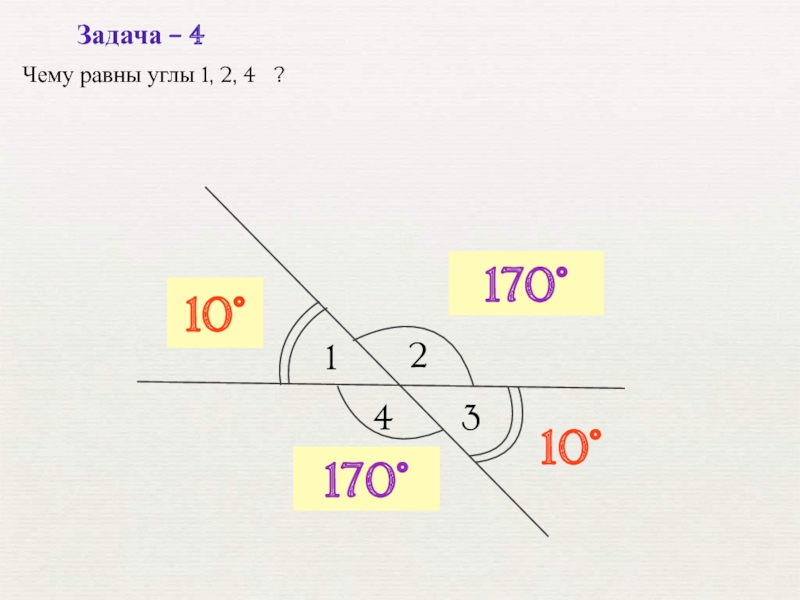
- 5. 1210°Задача – 4180°– 10°34???Чему равны углы 1, 2, 4 ?170°170°10°
- 6. Задача – 512?x3xх + 3х = 180°4х =
- 7. Задача – 612?4ххх + 4х = 180°5х =
- 8. Задача – 712?xх+30°х + (х + 30°) =
- 9. Задача – 8?xх– 50°х – 50° + х
- 10. ?Задача – 912?∠1 = ∠2Дано: ∠1 и ∠2
- 11. ?Задача – 10?∠2 – ∠1 = 20°Решение.Дано: ∠1
- 12. ?Задача – 11∠1+∠3=80°∠1 + ∠3 = 80°Решение.∠1 и
- 13. ?Задача – 12∠1 + ∠2 + ∠3 +
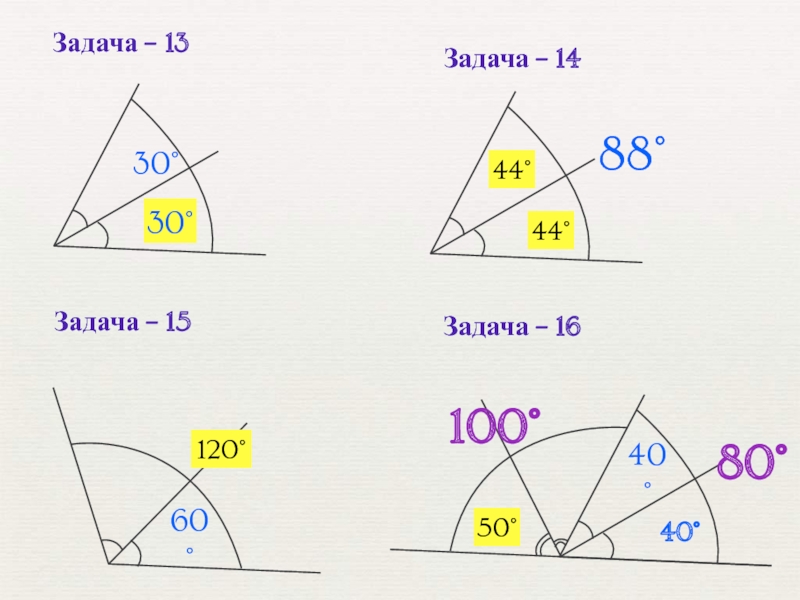
- 14. Задача – 1330°Задача – 16Задача – 15Задача – 1444°44°120°40°80°100°50°
- 15. Домашнее задание:п. 14 – 191) прочитать;2) знать
- 16. Спасибо за работу на уроке!
- 17. Скачать презентанцию
1265°?Задача – 1180°– 65°115°∠1 и ∠2 – смежные углы ∠1 + ∠2 = 180° (по теореме о смежных углах)Чему равен угол, если смежный с ним угол равен 65° ?
Слайды и текст этой презентации
Слайд 1Задачи
по теме
«Смежные и вертикальные углы»
Наганова Ирина Владимировна – учитель математики Каширской спецшколы
7
класс, Геометрия
Слайд 21
2
65°
?
Задача – 1
180°– 65°
115°
∠1 и ∠2 – смежные углы
∠1 +
∠2 = 180°
(по теореме о смежных углах)
Чему равен угол, если
смежный с ним угол равен 65° ?
Слайд 31
2
130°
?
Задача – 2
180°– 130°
50°
∠1 и ∠2 – смежные углы
∠1 +
∠2 = 180°
(по теореме о смежных углах)
Чему равен угол, если
смежный с ним угол равен 130° ?
Слайд 41
2
73°
?
Задача – 3
73°
∠1 и ∠2 – вертикальные углы
∠1 = ∠2 (по теореме
о
вертикальных углах)
Чему равен угол 2 ?
Слайд 6Задача – 5
1
2
?
x
3x
х + 3х = 180°
4х = 180°
х = 180°
: 4
х = 45°
∠2 = 180° – ∠1 = 180°
– 45° = 135°∠2 в 3 раза больше ∠1
– угол 1
45°
135°
Решение.
Ответ: ∠1 = 45°, ∠2 = 135°
Пусть ∠1 = х, тогда ∠2 = 3х
Дано: ∠1 и ∠2 – смежные
Найти: ∠1 и ∠2
∠1 + ∠2 = 180° (по теореме о смежных углах)
Один из смежных углов в 3 раза больше другого. Найдите эти углы.
Слайд 7Задача – 6
1
2
?
4х
х
х + 4х = 180°
5х = 180°
х = 180°
: 5
х = 36°
∠2 = 180° – ∠1 = 180°
– 36° = 144°∠1 в 4 раза меньше ∠2
– угол 1
144°
36°
Решение.
Ответ: ∠1 = 36°, ∠2 = 144°
Пусть ∠1 = х, тогда ∠2 = 4х
Дано: ∠1 и ∠2 – смежные
Найти: ∠1 и ∠2
∠1 + ∠2 = 180° (по теореме о смежных углах)
Один из смежных углов в 4 раза меньше другого. Найдите эти углы.
Слайд 8Задача – 7
1
2
?
x
х+30°
х + (х + 30°) = 180°
2х + 30°
= 180°
2х = 180° – 30°
х = 75°
∠2 = 180°
– ∠1 = 180° – 75° = 105°∠2 на 30° больше ∠1
– угол 1
75°
105°
Решение.
Ответ: ∠1 = 75°, ∠2 = 105°
Пусть ∠1 = х, тогда ∠2 = х + 30°
Дано: ∠1 и ∠2 – смежные
Найти: ∠1 и ∠2
∠1 + ∠2 = 180° (по теореме о смежных углах)
2х = 150°
х = 150° : 2
Один из смежных углов на 30° больше другого. Найдите эти углы.
Слайд 9Задача – 8
?
x
х– 50°
х – 50° + х = 180°
2х –
50° = 180°
2х = 180° + 50°
х = 115°
∠1 =
180° – ∠2 = 180° – 115° = 65°∠1 на 50° меньше ∠2
– угол 2
115°
65°
Решение.
Ответ: ∠1 = 65°, ∠2 = 115°
Пусть ∠2 = х, тогда ∠1 = х – 50°
Дано: ∠1 и ∠2 – смежные
Найти: ∠1 и ∠2
∠1 + ∠2 = 180° (по теореме о смежных углах)
2х = 230°
х = 230° : 2
Один из смежных углов на 50° меньше другого. Найдите эти углы.
Слайд 10?
Задача – 9
1
2
?
∠1 = ∠2
Дано: ∠1 и ∠2 – смежные
Найти: ∠1
и ∠2
Решение.
∠1 и ∠2 – смежные, тогда по теореме о
смежных углах имеем, что ∠1 + ∠2 = 180°.
По условию ∠1 = ∠2, тогда ∠1 = ∠2 = 180° : 2 = 90°
Ответ: ∠1 = 90°, ∠2 = 90°
Смежные углы равны. Найдите эти углы.
Слайд 11?
Задача – 10
?
∠2 – ∠1 = 20°
Решение.
Дано: ∠1 и ∠2 –
смежные
Найти: ∠1 и ∠2
x + 20°
х
х + (х + 20°)
= 180°2х + 20° = 180°
2х = 180° – 20°
х = 80°
∠2 = х + 20° = 80° + 20° = 100°
Ответ: ∠1 = 80°, ∠2 = 100°
2х = 160°
х = 160° : 2
100°
Пусть ∠1 = х, тогда ∠2 = х + 20°
∠1 + ∠2 = 180° (по теореме о смежных углах)
– угол 1
Разность двух смежных углов равна 30°. Найдите эти углы.
80°
Слайд 12?
Задача – 11
∠1+∠3=80°
∠1 + ∠3 = 80°
Решение.
∠1 и ∠2 – смежные
Найти:
40°
140°
∠3
и ∠2 – смежные
Чему равен угол, если два смежных с
ним угла в сумме дают 80° ?Дано:
∠2
∠1 = ∠3 = 80°: 2 = 40° (верт.)
40°
∠2 = 180° – ∠1 = 180° – 40° = 140° (смеж.)
∠2 = 180° – ∠3 = 180° – 40° = 140° (смеж.)
Ответ: ∠2 = 140°
или
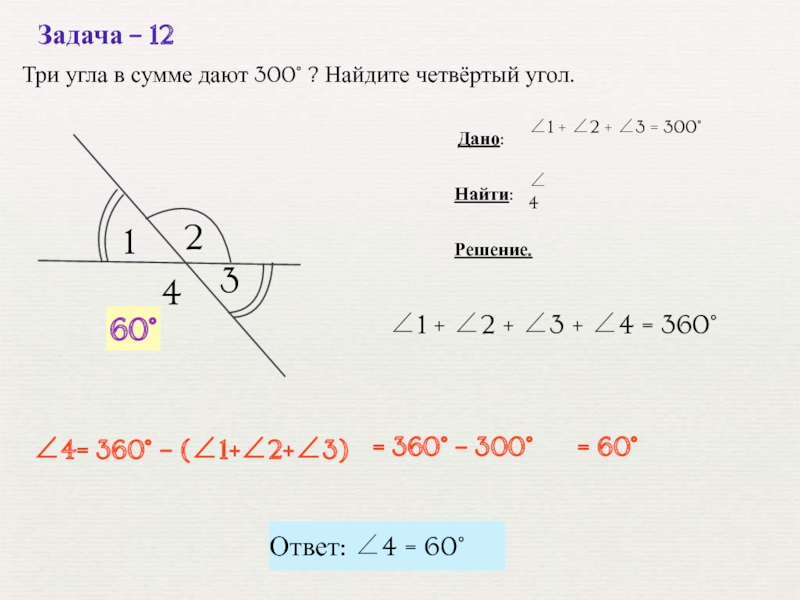
Слайд 13?
Задача – 12
∠1 + ∠2 + ∠3 + ∠4 = 360°
∠1
+ ∠2 + ∠3 = 300°
Решение.
Найти:
Три угла в сумме
дают 300° ? Найдите четвёртый угол.Дано:
60°
Ответ: ∠4 = 60°
∠4= 360° – (∠1+∠2+∠3)
= 360° – 300°
= 60°
∠4
Слайд 15Домашнее задание:
п. 14 – 19
1) прочитать;
2) знать все определения и
формулировки теорем.
стр. 26, № 4 (2), 8, 9, 10, 11,
12(решить любых 2 номера)
Похожие презентации
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое TheSlide.ru?
Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.