Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пифагор и его открытия 11 класс
Содержание
- 1. Пифагор и его открытия 11 класс
- 2. Для кого это пособие созданоПифагорейцы постоянно указывали,
- 3. Авторы надеются, что наше пособие поможет учащимся в изучении данной темы
- 4. Великий древнегреческий учёный Пифагор (570-496г. до н.э.)
- 5. Великий древнегреческий учёный Пифагор (570-496г. до н.э.)родился
- 6. Немного историиПо своим политическим взглядам Пифагор был
- 7. Древнегреческая религиозно-философская школаОколо 530 г. до н.
- 8. Пифагорейцы также занимались теорией музыки, скульптуры и
- 9. Слайд 9
- 10. Правило «Золотого сечения»Если отрезок АС разделен в
- 11. Среди своих сторонников и последователей пользовался непререкаемым
- 12. Много сделал Пифагор и в развитии геометрии.
- 13. Слайд 13
- 14. Вклад учёного в развитие математикиВсе числа Пифагор
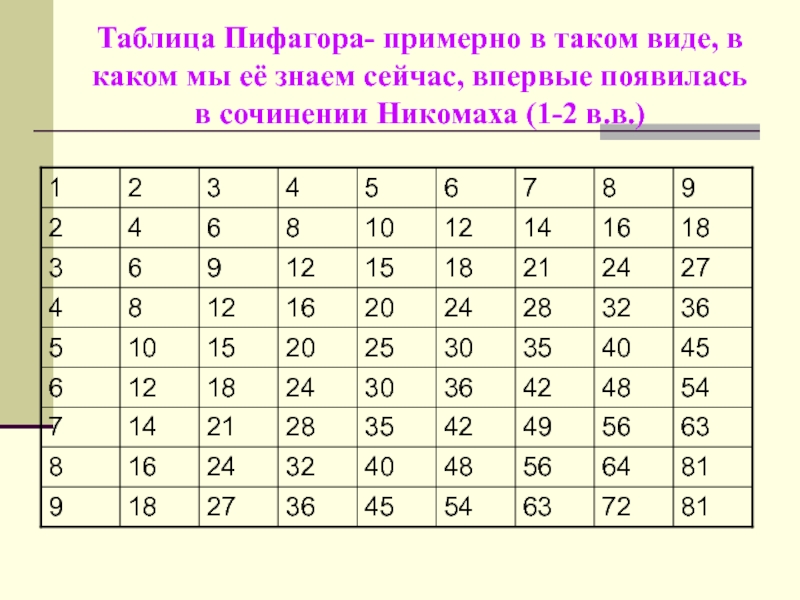
- 15. Таблица Пифагора- примерно в таком виде, в
- 16. Теорема Пифагора Представить себе эту
- 17. Теорема Пифагора:В прямоугольном треугольнике квадрат гипотенузы равен
- 18. «Начала» ЕвклидаЗдесь теорема дана в следующей формулировке:
- 19. Доказательство теоремы Пифагора, данное Леонардо да
- 20. Доказательство теоремы Пифагора индийским математиком XII в.
- 21. Доказательство на основе подобия:
- 22. Примеры решения задач:САВДано: Δ АВС- прямоугольный,
- 23. Реши, применив теорему Пифагора, к задачам
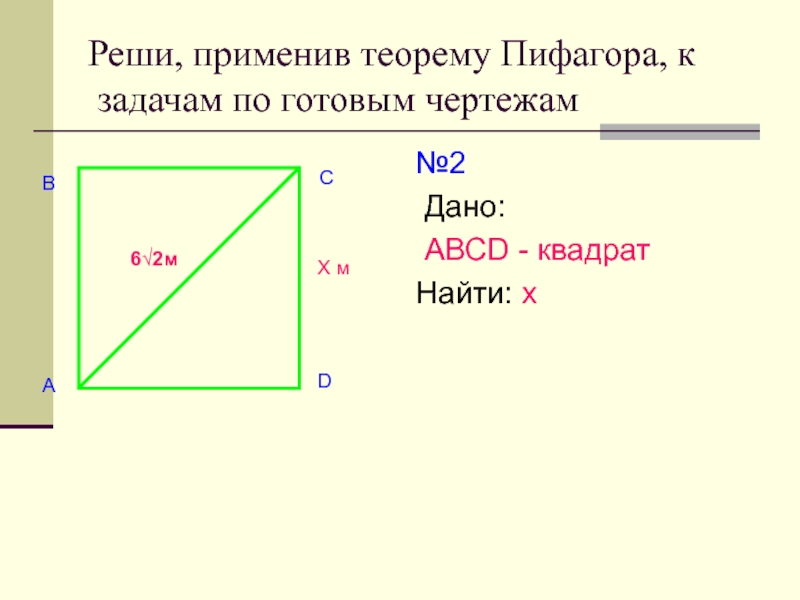
- 24. Реши, применив теорему Пифагора, к задачам по готовым чертежам№2 Дано: АВСD - квадратНайти: хВАСDХ м6√2м
- 25. Литература:Учебник для 7-9 классов « Геометрия», Л.С.
- 26. Авторы:Остермиллер Елена Ивановна- учитель математики МОУ «Средняя
- 27. Скачать презентанцию
Для кого это пособие созданоПифагорейцы постоянно указывали, что правильное обучение должно возникать по обоюдному желанию учителя и учащегося, ибо если та или иная сторона противится, то изучение наук будет негодным и
Слайды и текст этой презентации
Слайд 5Великий древнегреческий учёный Пифагор (570-496г. до н.э.)родился на острове Самос
Значительную
часть своей жизни провел на острове Самос.
При тиране Поликрате переселился
в Южную Италию в город КратонСлайд 6Немного истории
По своим политическим взглядам Пифагор был на стороне аристократов.
Он
выдвинул учение о "порядке", считая, что только власть аристократов обеспечивает
этот порядок в общественной жизни Демократия же - это нарушение порядка.Слайд 7Древнегреческая религиозно-философская школа
Около 530 г. до н. э. Пифагор переехал
в Кротон- греческую колонию в южной Италии, где основал так
называемый пифагорейский союз.Деятельность союза была окружена тайной, поэтому кто на самом деле являлся автором того или иного результата неизвестно.
Слайд 8Пифагорейцы также занимались теорией музыки, скульптуры и архитектуры. Они внесли
свой значительный вклад в теорию изобразительного искусства в отношении проблемы
"золотого сечения"Слайд 10Правило «Золотого сечения»
Если отрезок АС разделен в точке В, то
отношение отрезка АВ к ВС должно быть таким, как и
отношение всего отрезка АС к ВС).Правило «золотого сечения» соблюдается при конструировании отдельных частей зданий и скульптурных групп.
Слайд 11Среди своих сторонников и последователей пользовался непререкаемым авторитетом (в пословицу
вошло выражение: "Сам сказал").
Вокруг имени Пифагора существует немало легенд.
Слайд 12Много сделал Пифагор и в развитии геометрии.
Считается, что Пифагор
был первым европейцем, который настаивал на выборе некоторых аксиом и
на последующем построении высказываний с помощью дедуктивного рассуждения, т.е. ввел в математику доказательство, что было величайшим достижением.Слайд 13
В противоположность
ионийским мыслителям, которые первоосновой явлений природы считали отдельные вещества -
воду, воздух, огонь - Пифагор основой всего сущего рассматривал числа, являющиеся, по его мнению, тем фундаментом, который образует порядок во Вселенной и обществе.Слайд 14Вклад учёного в развитие математики
Все числа Пифагор разделял на четные
и нечетные.
Основой всех чисел признавал единицу, которая рассматривалась как
четно-нечетное число. Единица - это священная монада, выступавшая в качестве первоначала и основы окружающего мира. Числа выступали как реальная сущность всех вещей.
Пифагор и пифагорейцы заложили основы теории чисел и принципы арифметики.
Слайд 15Таблица Пифагора- примерно в таком виде, в каком мы её
знаем сейчас, впервые появилась в сочинении Никомаха (1-2 в.в.)
Слайд 16Теорема Пифагора
Представить себе эту теорему отдельно от
имени великого грека уже невозможно, но на самом деле соотношение,
которое она утверждает, было известно древним математикам за много веков до Пифагора. О наиболее известном частном случае теоремы — «египетском треугольнике» со сторонами 3, 4 и 5 — говорится в папирусе, который историки относят к 2000 г. до н.э. То же соотношение встречается и на вавилонских клинописных табличках, и в древнекитайских, и в древнеиндийских трактатах. Однако в современной истории математики считается, что именно Пифагор дал его первое логически стройное доказательство. Со времен Пифагора появились сотни доказательств знаменитой теоремы, она даже попала в Книгу рекордов Гиннеса. Однако принципиально различных идей в этих доказательствах используется сравнительно немного.Слайд 17Теорема Пифагора:
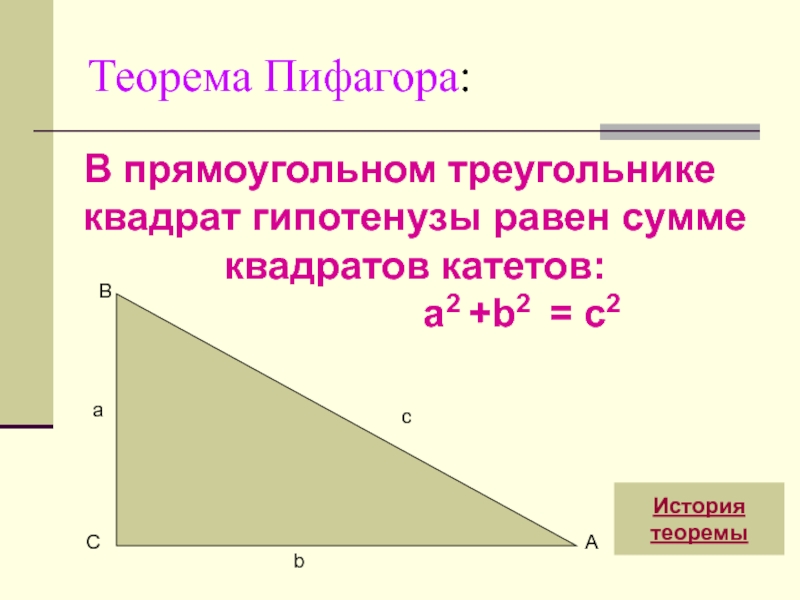
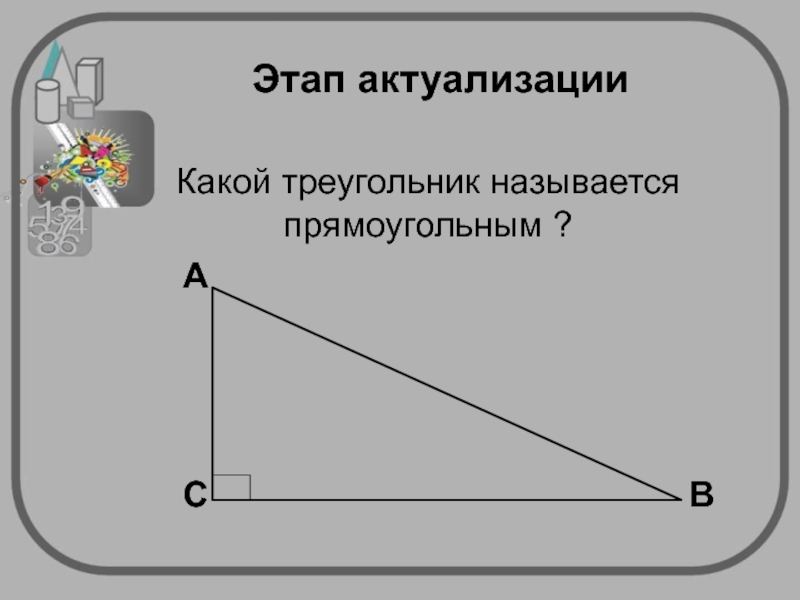
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
a2 +b2 = c2
а
b
c
C
A
B
История
теоремы
Слайд 18«Начала» Евклида
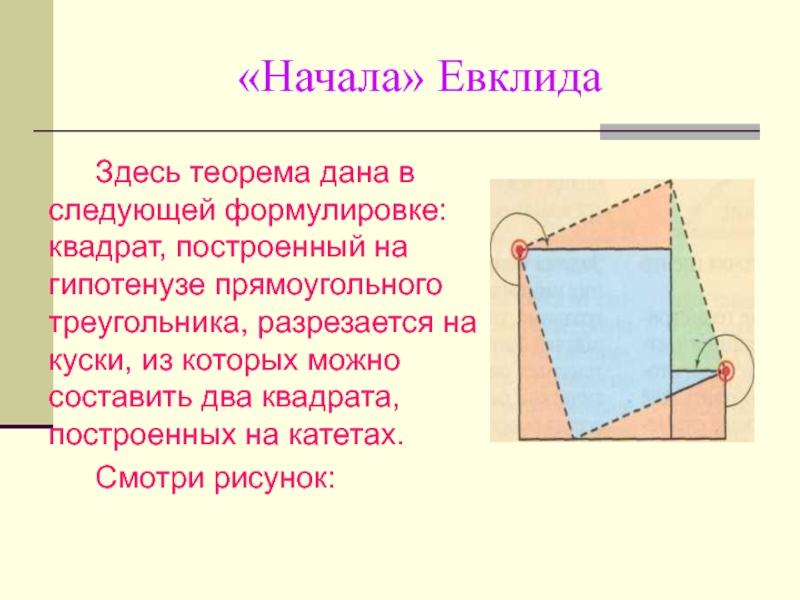
Здесь теорема дана в следующей формулировке: квадрат, построенный на
гипотенузе прямоугольного треугольника, разрезается на куски, из которых можно составить
два квадрата, построенных на катетах.Смотри рисунок:
Слайд 19Доказательство теоремы Пифагора,
данное Леонардо да Винчи.
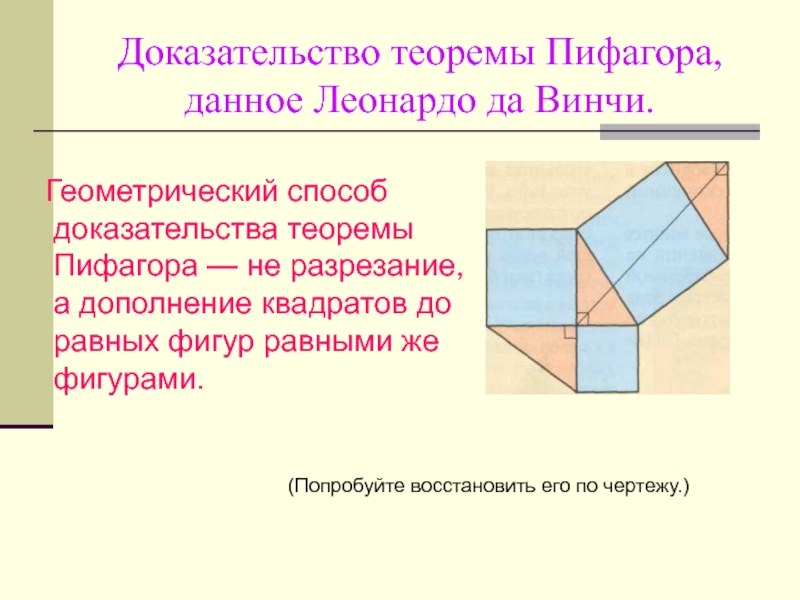
Геометрический способ
доказательства теоремы Пифагора — не разрезание, а дополнение квадратов до
равных фигур равными же фигурами.(Попробуйте восстановить его по чертежу.)
Слайд 20Доказательство теоремы Пифагора индийским математиком XII в. Бхаскара
В этом доказательстве
используются формулы для вычисления площади, т. е. геометрия в них
сочетается с алгеброй.Оно знаменито тем, что весь текст к чертежу состоит из единственного слова «Смотри!».
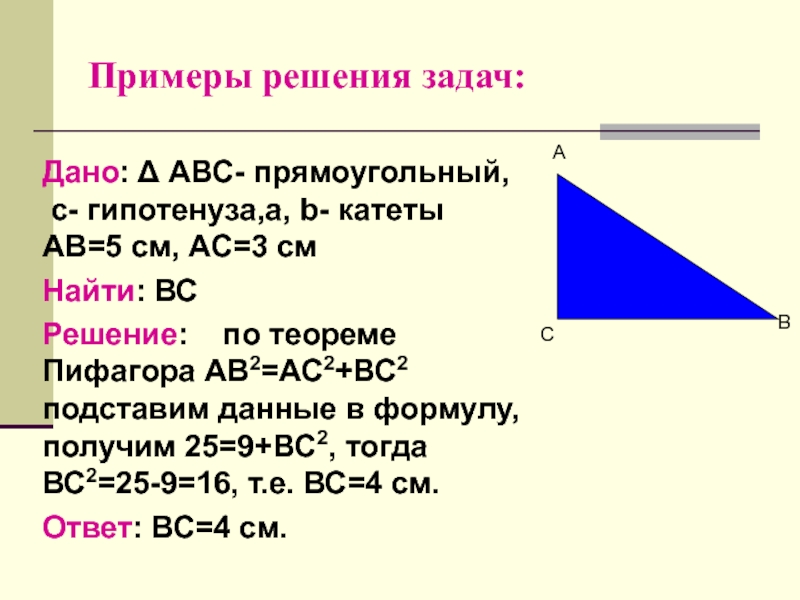
Слайд 22Примеры решения задач:
С
А
В
Дано: Δ АВС- прямоугольный,
с- гипотенуза,a, b- катеты
АВ=5
см, АС=3 см
Найти: ВС
Решение: по теореме Пифагора АВ2=АС2+ВС2
подставим данные в формулу, получим 25=9+ВС2, тогда ВС2=25-9=16, т.е. ВС=4 см.Ответ: ВС=4 см.
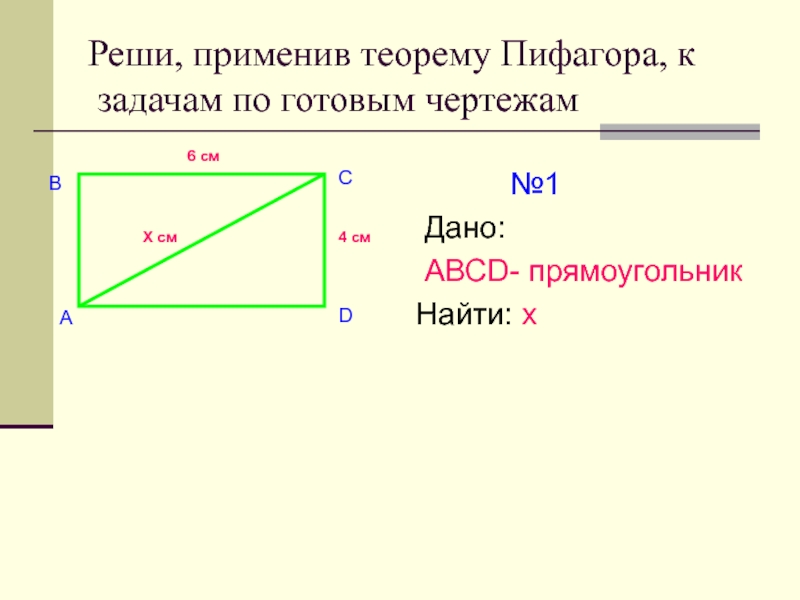
Слайд 23Реши, применив теорему Пифагора, к
задачам по готовым чертежам
№1
Дано:
АВСD- прямоугольник
Найти: х
А
В
С
D
Х см
6
см4 см