Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие вписанного и описанного шара 11 класс
Содержание
- 1. Понятие вписанного и описанного шара 11 класс
- 2. Слайд 2
- 3. ПОНЯТИЕ ВПИСАННОЙ ОКРУЖНОСТИ,Центр окружности, вписанной в треугольник,
- 4. ПОНЯТИЕ ОПИСАННОЙ ОКРУЖНОСТИЦентр окружности, описанной
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
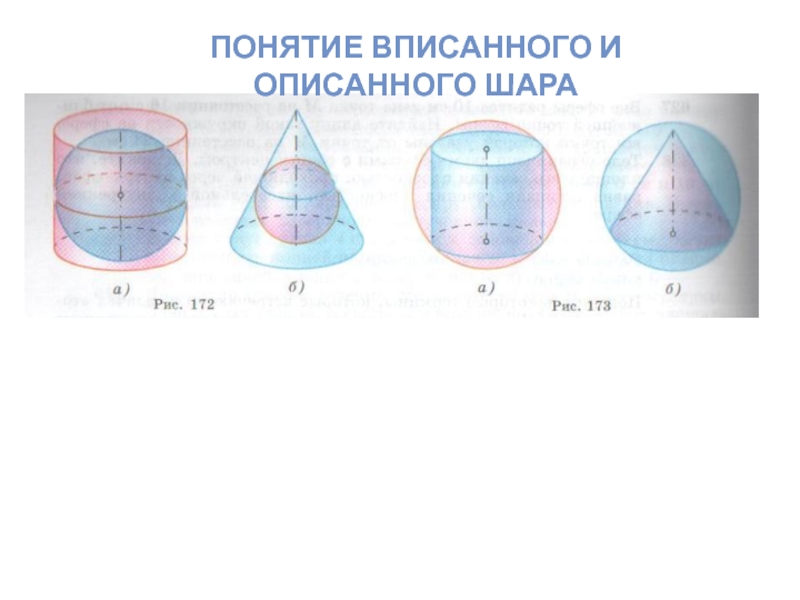
- 8. ПОНЯТИЕ ВПИСАННОГО И ОПИСАННОГО ШАРА
- 9. Слайд 9
- 10. Слайд 10
- 11. Скачать презентанцию
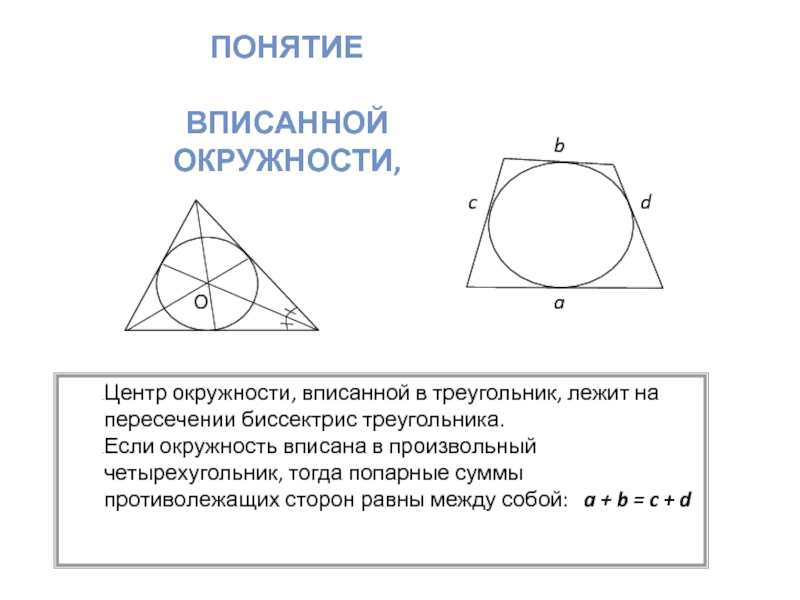
ПОНЯТИЕ ВПИСАННОЙ ОКРУЖНОСТИ,Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c +
Слайды и текст этой презентации
Слайд 3ПОНЯТИЕ
ВПИСАННОЙ ОКРУЖНОСТИ,
Центр окружности, вписанной в треугольник, лежит на пересечении
биссектрис треугольника.
Если окружность вписана в произвольный четырехугольник, тогда попарные суммы
противолежащих сторон равны между собой: a + b = c + dСлайд 4ПОНЯТИЕ ОПИСАННОЙ ОКРУЖНОСТИ
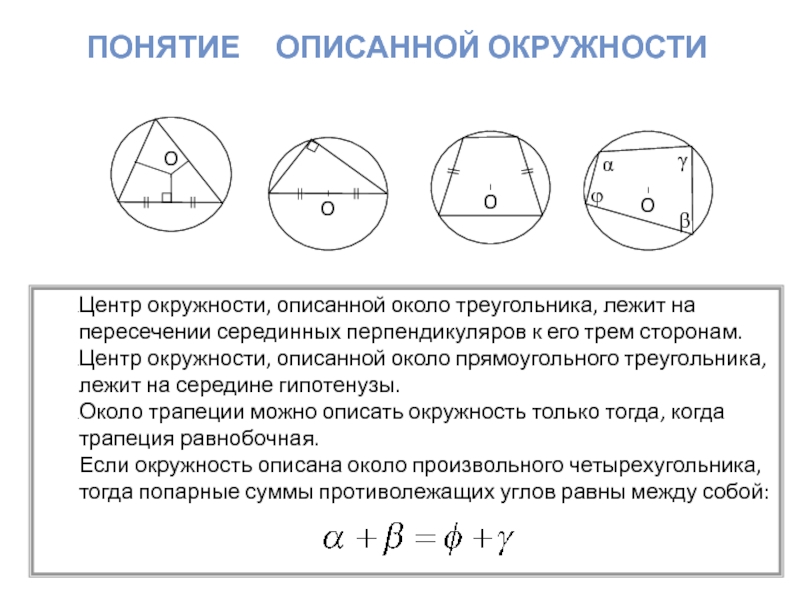
Центр окружности, описанной около треугольника, лежит
на пересечении серединных перпендикуляров к его трем сторонам.
Центр окружности, описанной
около прямоугольного треугольника, лежит на середине гипотенузы.Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой: