Двугранный угол

Содержание

1. Двугранный угол
2. Упражнение 1Какой угол образует ребро двугранного угла
3. Упражнение 2Плоскости двух равнобедренных треугольников с общим
4. Упражнение 3Треугольник MAB и квадрат ABCD заданы
5. Упражнение 4В правильной треугольной призме найдите угол между боковыми гранями.Ответ: 60о.
6. Упражнение 5В кубе A…D1 найдите угол наклона плоскости ABC1 к плоскости ABC.Ответ: 45о.
7. Упражнение 6Найдите двугранные углы правильного тетраэдра.
8. Упражнение 7Найдите геометрическое место точек в пространстве,
9. Упражнение 8Через сторону BC треугольника ABC проведена
10. Упражнение 9Через катет BC=a равнобедренного прямоугольного треугольника
11. Упражнение 10Через сторону BC треугольника ABC проведена
12. Упражнение 11Дан квадрат ABCD, через вершину D
13. Упражнение 12Основанием высоты четырехугольной пирамиды является точка
14. Упражнение 13В основании прямой призмы параллелограмм со
15. Упражнение 14Боковое ребро прямой призмы равно 6
16. Упражнение 15Сторона основания правильной треугольной призмы равна
17. Упражнение 16Ребро куба равно a. Найдите площадь
18. Упражнение 17Через середины двух смежных сторон основания
19. Упражнение 18Найдите двугранные углы октаэдра.
20. Упражнение 19Найдите двугранные углы икосаэдра.
21. Упражнение 20Найдите двугранные углы додекаэдра.
22. Скачать презентанцию

Упражнение 1Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного угла?Ответ: 90о.

Слайды и текст этой презентации

Слайд 1ДВУГРАННЫЙ УГОЛ
Двугранным углом называется фигура (рис. 1), образованную двумя полуплоскостями,

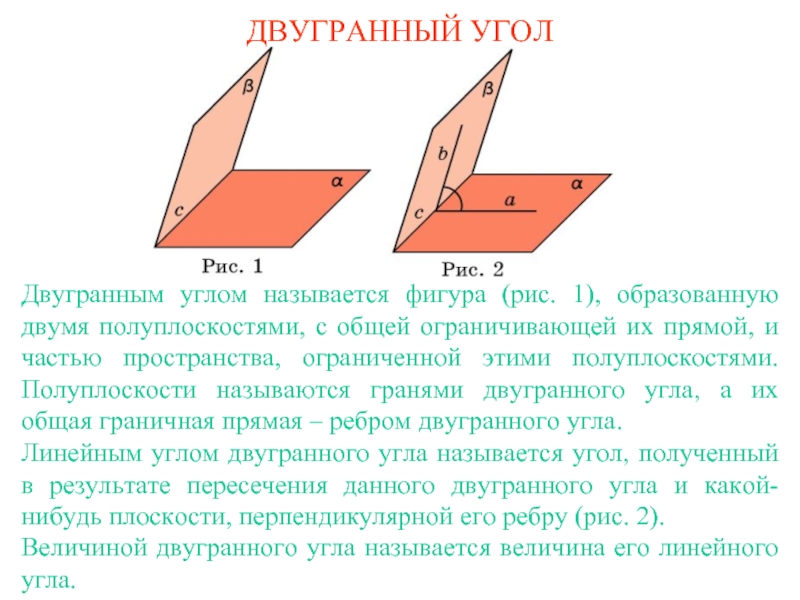
с общей ограничивающей их прямой, и частью пространства, ограниченной этими

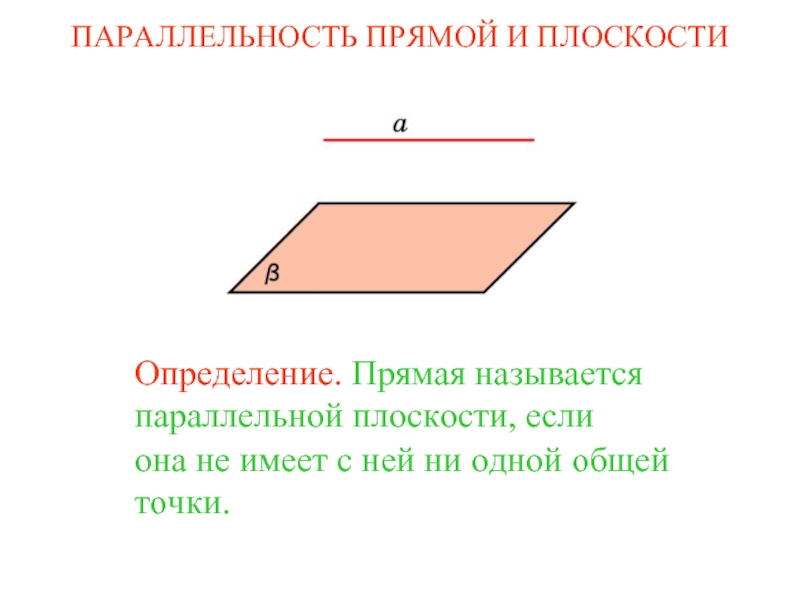
полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая граничная прямая – ребром двугранного угла.

Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2).

Величиной двугранного угла называется величина его линейного угла.

ДВУГРАННЫЙ УГОЛДвугранным углом называется фигура (рис. 1), образованную двумя полуплоскостями, с общей ограничивающей их прямой, и частью

Слайд 2Упражнение 1
Какой угол образует ребро двугранного угла с любой прямой,

лежащей в плоскости его линейного угла?
Ответ: 90о.

Слайд 3Упражнение 2
Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный

угол. Верно ли утверждение о том, что высоты, проведенные к

общему основанию треугольников, образуют линейный угол двугранного угла?

Ответ: Да.

Упражнение 2Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный угол. Верно ли утверждение о том, что

Слайд 4Упражнение 3
Треугольник MAB и квадрат ABCD заданы таким образом, что

MB - перпендикуляр к плоскости квадрата. Какой угол можно считать

углом между плоскостями AMD и ABC?

Ответ: MBC.

Упражнение 3Треугольник MAB и квадрат ABCD заданы таким образом, что MB - перпендикуляр к плоскости квадрата. Какой

Слайд 5Упражнение 4
В правильной треугольной призме найдите угол между боковыми гранями.
Ответ:

60о.

Слайд 6Упражнение 5
В кубе A…D1 найдите угол наклона плоскости ABC1 к

плоскости ABC.
Ответ: 45о.

Слайд 7Упражнение 6
Найдите двугранные углы правильного тетраэдра.

Слайд 8Упражнение 7
Найдите геометрическое место точек в пространстве, равноудаленных от двух

пересекающихся плоскостей.
Ответ: Две биссектральные плоскости.

Упражнение 7Найдите геометрическое место точек в пространстве, равноудаленных от двух пересекающихся плоскостей. Ответ: Две биссектральные плоскости.

Слайд 9Упражнение 8
Через сторону BC треугольника ABC проведена плоскость α под

углом 30° к плоскости треугольника. Высота AD треугольника ABC равна

a. Найдите расстояние от вершины A треугольника до плоскости α.

Упражнение 8Через сторону BC треугольника ABC проведена плоскость α под углом 30° к плоскости треугольника. Высота AD

Слайд 10Упражнение 9
Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C

равен 90°) проведена плоскость α, образующая с плоскостью треугольника угол

30°. Найдите расстояние от вершины A до плоскости α.

Упражнение 9Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C равен 90°) проведена плоскость α, образующая с

Слайд 11Упражнение 10
Через сторону BC треугольника ABC проведена плоскость под углом

30° к плоскости треугольника; угол C равен 150°, AC =

6. Найдите расстояние от вершины A до этой плоскости.

Ответ: 1,5.

Упражнение 10Через сторону BC треугольника ABC проведена плоскость под углом 30° к плоскости треугольника; угол C равен

Слайд 12Упражнение 11
Дан квадрат ABCD, через вершину D параллельно диагонали AC

проведена плоскость α, образующая с диагональю BD угол 60°. Чему

равен угол между плоскостью квадрата и плоскостью α?

Ответ: 60о.

Упражнение 11Дан квадрат ABCD, через вершину D параллельно диагонали AC проведена плоскость α, образующая с диагональю BD

Слайд 13Упражнение 12
Основанием высоты четырехугольной пирамиды является точка пересечения диагоналей основания

пирамиды. Верно ли, что двугранные углы, образованные боковыми гранями пирамиды

с плоскостью основания, равны, если основанием пирамиды является: а) квадрат; б) параллелограмм; в) ромб; г) равнобедренная трапеция?

Ответ: а) Да;

б) нет;

в) да;

г) нет.

Упражнение 12Основанием высоты четырехугольной пирамиды является точка пересечения диагоналей основания пирамиды. Верно ли, что двугранные углы, образованные

Слайд 14Упражнение 13
В основании прямой призмы параллелограмм со сторонами 4 дм

и 5 дм. Угол между ними 30°. Найдите площадь сечения

призмы плоскостью, если известно, что она пересекает все боковые ребра и образует с плоскостью основания угол 45°.

Упражнение 13В основании прямой призмы параллелограмм со сторонами 4 дм и 5 дм. Угол между ними 30°.

Слайд 15Упражнение 14
Боковое ребро прямой призмы равно 6 см. Ее основание

– прямоугольный треугольник с катетами 3 см и 2 см.

Найдите площади сечений призмы плоскостями, проходящими через каждый из данных катетов и образующими углы 60° с плоскостью основания.

Ответ: 6 см2.

Упражнение 14Боковое ребро прямой призмы равно 6 см. Ее основание – прямоугольный треугольник с катетами 3 см

Слайд 16Упражнение 15
Сторона основания правильной треугольной призмы равна 4 см. Найдите

площадь сечения призмы плоскостью, проходящей через середины двух сторон основания

и образующей угол 45° с его плоскостью, если известно, что плоскость пересекает: а) только одно боковое ребро призмы; б) два ее боковых ребра.

Упражнение 15Сторона основания правильной треугольной призмы равна 4 см. Найдите площадь сечения призмы плоскостью, проходящей через середины

Слайд 17Упражнение 16
Ребро куба равно a. Найдите площадь сечения куба плоскостью,

проходящей через сторону основания, если угол между этой плоскостью и

плоскостью основания равен: а) 30°; б) ϕ.

Упражнение 16Ребро куба равно a. Найдите площадь сечения куба плоскостью, проходящей через сторону основания, если угол между

Слайд 18Упражнение 17
Через середины двух смежных сторон основания правильной четырехугольной призмы

проведена плоскость, образующая с плоскостью основания угол ϕ и пересекающая

три боковых ребра призмы. Найдите сторону основания, если площадь сечения равна Q.

Упражнение 17Через середины двух смежных сторон основания правильной четырехугольной призмы проведена плоскость, образующая с плоскостью основания угол

Слайд 19Упражнение 18
Найдите двугранные углы октаэдра.

Слайд 20Упражнение 19
Найдите двугранные углы икосаэдра.

Слайд 21Упражнение 20
Найдите двугранные углы додекаэдра.

Скачать презентацию

Теги

Разделы презентаций

Двугранный угол

Содержание

Слайды и текст этой презентации

Слайд 1ДВУГРАННЫЙ УГОЛДвугранным углом называется фигура (рис. 1), образованную двумя полуплоскостями,

с общей ограничивающей их прямой, и частью пространства, ограниченной этими

Слайд 2Упражнение 1Какой угол образует ребро двугранного угла с любой прямой,

лежащей в плоскости его линейного угла?Ответ: 90о.

Слайд 3Упражнение 2Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный

угол. Верно ли утверждение о том, что высоты, проведенные к

Слайд 4Упражнение 3Треугольник MAB и квадрат ABCD заданы таким образом, что

MB - перпендикуляр к плоскости квадрата. Какой угол можно считать

Слайд 5Упражнение 4В правильной треугольной призме найдите угол между боковыми гранями.Ответ:

60о.

Слайд 6Упражнение 5В кубе A…D1 найдите угол наклона плоскости ABC1 к

плоскости ABC.Ответ: 45о.

Слайд 7Упражнение 6Найдите двугранные углы правильного тетраэдра.

Слайд 8Упражнение 7Найдите геометрическое место точек в пространстве, равноудаленных от двух

пересекающихся плоскостей. Ответ: Две биссектральные плоскости.

Слайд 9Упражнение 8Через сторону BC треугольника ABC проведена плоскость α под

углом 30° к плоскости треугольника. Высота AD треугольника ABC равна

Слайд 10Упражнение 9Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C