Разделы презентаций

Комбинации геометрических тел

Содержание

Цилиндр и призмаЦилиндр, описанный около призмыЦилиндр, вписанный в призму

Слайды и текст этой презентации

Слайд 1Комбинации геометрических тел
Вписанные и описанные тела

Комбинации геометрических телВписанные и описанные тела

Слайд 2Цилиндр и призма
Цилиндр, описанный
около призмы
Цилиндр, вписанный
в призму

Цилиндр и призмаЦилиндр, описанный около призмыЦилиндр, вписанный в призму

Слайд 3Конус и пирамида
Конус, описанный
около пирамиды
Конус, вписанный
в пирамиду
R

Конус и пирамидаКонус, описанный около пирамидыКонус, вписанный в пирамидуR

Слайд 4Шар и цилиндр














Шар и цилиндр

Слайд 5Шар, описанный около цилиндра
Радиус шара R,
радиус цилиндра r,
высота цилиндра

H
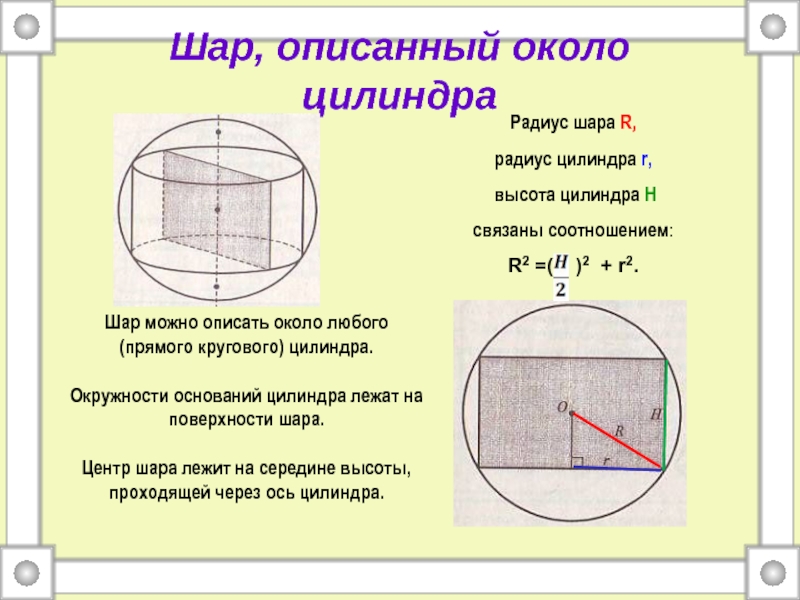
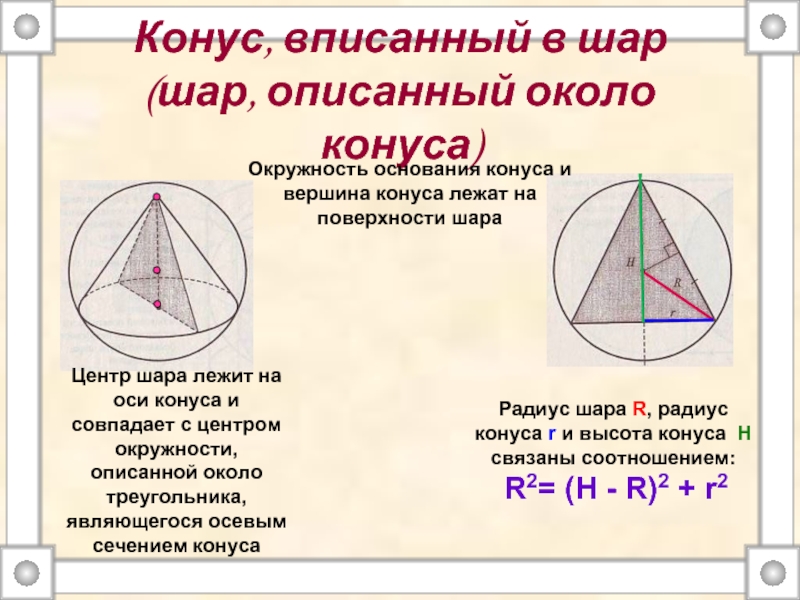
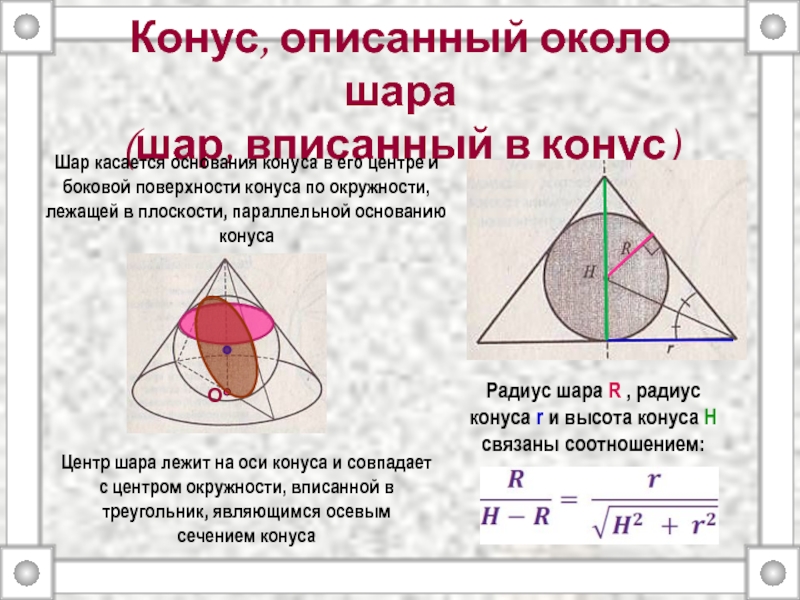
связаны соотношением:
R2 =( )2 + r2.

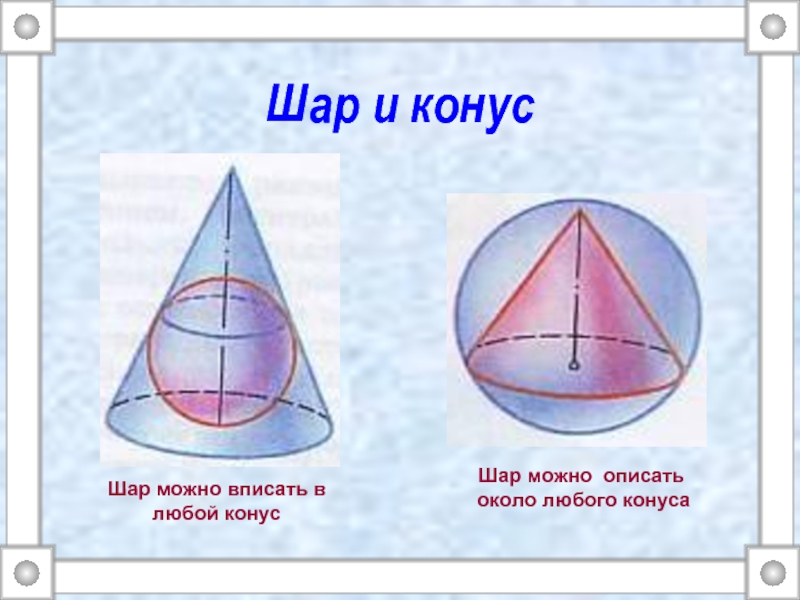
Шар можно описать около

любого (прямого кругового) цилиндра.

Окружности оснований цилиндра лежат на поверхности шара.

Центр шара лежит на середине высоты, проходящей через ось цилиндра.
Шар, описанный около цилиндраРадиус шара R,радиус цилиндра r, высота цилиндра Hсвязаны соотношением:R2 =( )2 + r2.Шар

Слайд 6Шар, вписанный в цилиндр
Радиус шара R равен радиусу цилиндра r,

а диаметр шара равен высоте цилиндра:
R = r

2R = H

Шар можно вписать только в такой цилиндр, высота которого равна диаметру основания
( такой цилиндр называется равносторонним)

Шар касается оснований в их центрах и боковой поверхности цилиндра по окружности большого круга шара, параллельной основаниям цилиндра




Шар, вписанный в цилиндрРадиус шара R равен радиусу цилиндра r, а диаметр шара равен высоте цилиндра: R

Слайд 7Шар и конус
Шар можно описать
около любого конуса
Шар можно вписать

в любой конус

Шар и конусШар можно описать около любого конусаШар можно вписать в любой конус

Слайд 8Конус, вписанный в шар (шар, описанный около конуса)



Окружность основания конуса и

вершина конуса лежат на поверхности шара
Центр шара лежит на оси

конуса и совпадает с центром окружности, описанной около треугольника, являющегося осевым сечением конуса

Радиус шара R, радиус конуса r и высота конуса H связаны соотношением:
R2= (H - R)2 + r2

Конус, вписанный в шар (шар, описанный около конуса)Окружность основания конуса и вершина конуса лежат на поверхности шараЦентр

Слайд 9Конус, описанный около шара (шар, вписанный в конус)
О

Шар касается основания конуса

в его центре и боковой поверхности конуса по окружности, лежащей

в плоскости, параллельной основанию конуса



Центр шара лежит на оси конуса и совпадает с центром окружности, вписанной в треугольник, являющимся осевым сечением конуса


Радиус шара R , радиус конуса r и высота конуса H связаны соотношением:









Конус, описанный около шара (шар, вписанный в конус)ОШар касается основания конуса в его центре и боковой поверхности
Теги

Похожие презентации

Зеркальный мир в геометрии или симметрия (симметрия относительно прямой) Зеркальный мир в геометрии или симметрия (симметрия относительно прямой) 325
Правильные фигуры и тела Правильные фигуры и тела 517
Прямая и отрезок. Луч и угол. Сравнение и измерение отрезков и углов 7 класс Прямая и отрезок. Луч и угол. Сравнение и измерение отрезков и углов 7 класс 320
Площадь квадрата, прямоугольника, параллелограмма Площадь квадрата, прямоугольника, параллелограмма 387
Окружности Окружности 438
Многогранники Многогранники 657
Решение задач по теме Решение задач по теме "Смежные и вертикальные углы" 456
Презентация к уроку Презентация к уроку "Развертка и площадь поверхности цилиндра" 577
Площадь прямоугольника Площадь прямоугольника 357
Задачи на построение сечений Задачи на построение сечений 785
Окружность. Вписанные углы 7 класс Окружность. Вписанные углы 7 класс 333
Счастливый случай 7 класс Счастливый случай 7 класс 328
Төртбұрыш аудандарын табу Төртбұрыш аудандарын табу 701
Движения 9 класс Движения 9 класс 305
Метод координат Метод координат 533
Векторы в пространстве Векторы в пространстве 351
Геометрия на службе у архитектуры Геометрия на службе у архитектуры 481
Построение сечений параллелепипеда. Построение сечений параллелепипеда. 505
Плоскость, прямая, луч 5 класс Плоскость, прямая, луч 5 класс 440
Тренажер Тренажер "Координаты вектора" 9 класс УМК Атанасян Л.С 481

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика