Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Шар
Содержание
- 1. Шар
- 2. ROСферой называется поверхность, состоящая из всех точек
- 3. Сфера получена вращением полуокружности АСВ вокруг диаметра
- 4. RM(x;y;z)C(x0;y0;z0)zyxOУравнение сферыУравнение с тремя неизвестными x, y
- 5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИαyxzC (0;0;d)OR1d <
- 6. αROСечение шара плоскостью есть круг.Если секущая плоскость
- 7. OdC (0;0;d)αyxzd = RТогда R2 – d2
- 8. αyxdzC (0;0;d)O3d > RТогда R2 – d2
- 9. αОАКасательная плоскость к сфереПлоскость, имеющая со сферой
- 10. За площадь сферы примем предел последовательности площадей
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. BORrxMAxСОБЪЁМ ШАРАРассмотрим шар радиуса R и центром
- 15. СОВαхАВ = hАШаровым сегментом называется часть шара,
- 16. шаровойслойСВАШаровым слоем называется часть шара, заключённая между
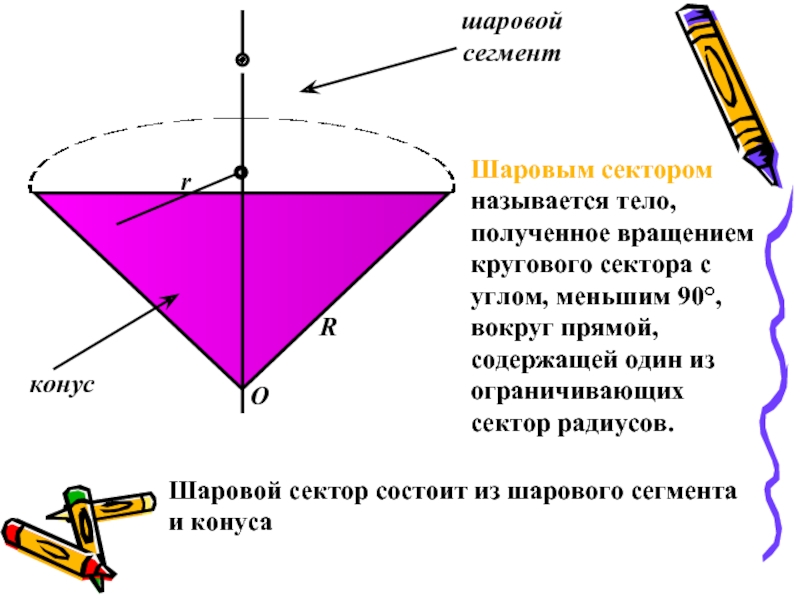
- 17. конусшаровойсегментOrRШаровым сектором называется тело, полученное вращением кругового
- 18. Скачать презентанцию
ROСферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точкиДанная точка называется центром сферыДанное расстояние – радиусом сферыОтрезок, соединяющий две точки сферы и проходящий через её
Слайды и текст этой презентации
Слайд 1ШАР
Мультимедийное пособие по стереометрии для 11 класса
учителя математики
МОУ «СОШ
№ 15» г.Братска
Слайд 2
R
O
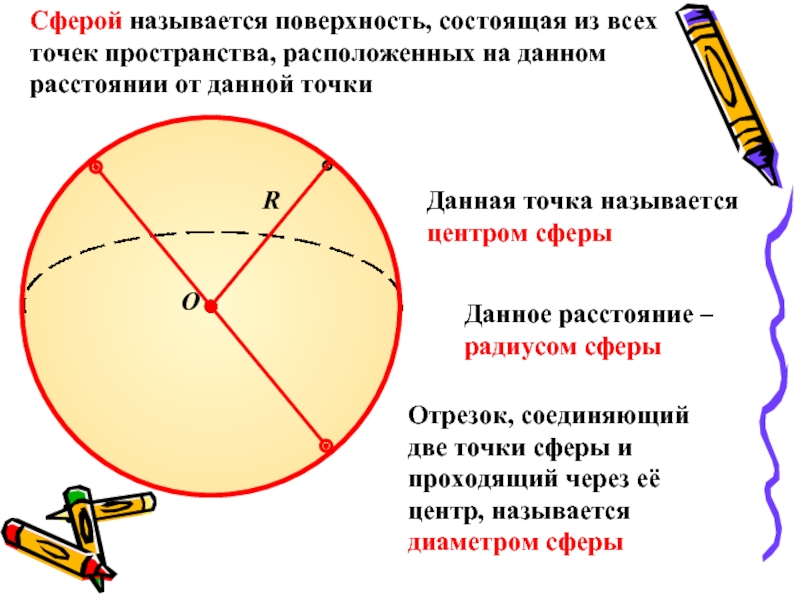
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на
данном расстоянии от данной точки
Данная точка называется центром сферы
Данное расстояние
– радиусом сферыОтрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы
Слайд 3
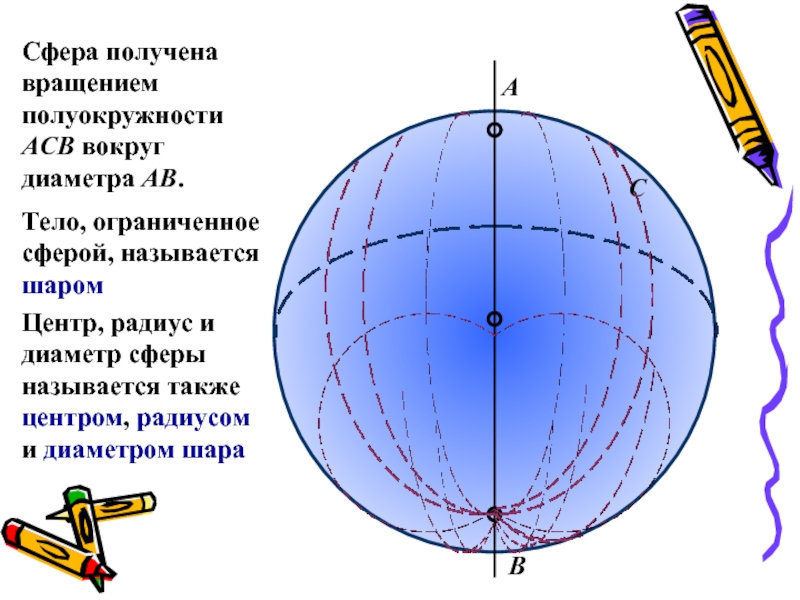
Сфера получена вращением полуокружности АСВ вокруг диаметра АВ.
А
С
В
Тело, ограниченное сферой,
называется шаром
Центр, радиус и диаметр сферы называется также центром, радиусом
и диаметром шара
Слайд 4
R
M(x;y;z)
C(x0;y0;z0)
z
y
x
O
Уравнение сферы
Уравнение с тремя неизвестными x, y и z называется
уравнением поверхности F
МС =
Если точка М лежит на данной сфере,
то МС = R или МС2 = R2, т.е. координаты точки М удовлетворяют уравнению(х – х0)2+(у – у0)2+(z – z0)2 =R2
Если точка М не лежит на данной сфере, то МС2 ≠ R2, т.е. координаты точки М не удовлетворяют уравнению.
Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром С(х0;у0;z0) имеет вид
(х – х0)2+(у – у0)2+(z – z0)2 =R2
Слайд 5ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ
α
y
x
z
C (0;0;d)
O
R
1
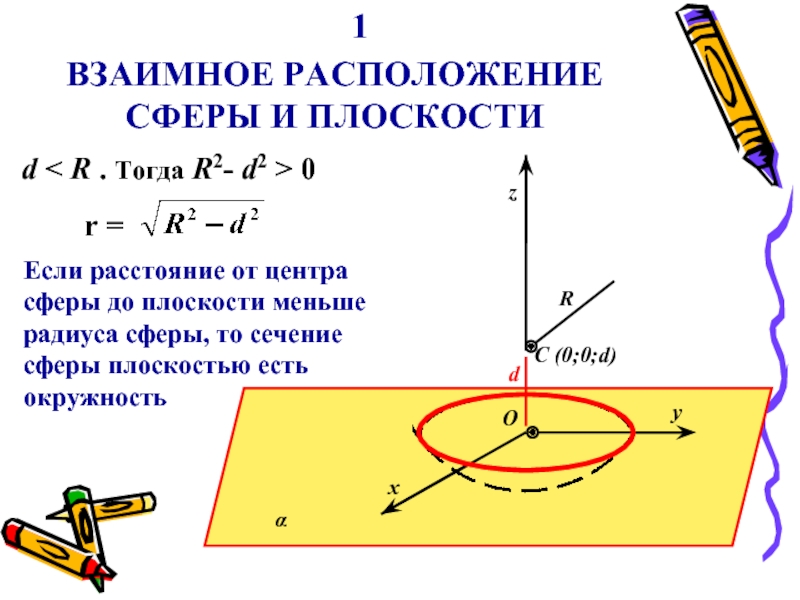
d < R . Тогда
R2- d2 > 0
r =
Если расстояние от центра сферы
до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружностьd
Слайд 6
α
R
O
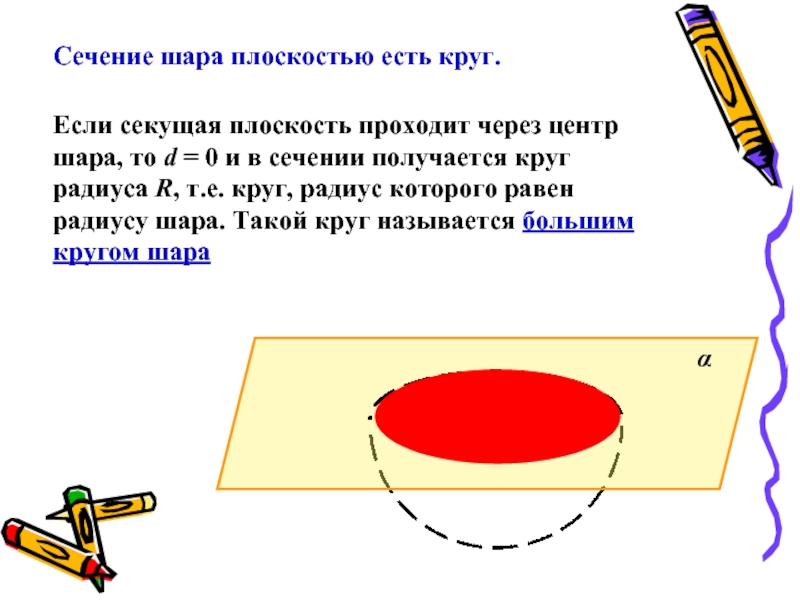
Сечение шара плоскостью есть круг.
Если секущая плоскость проходит через центр
шара, то d = 0 и в сечении получается круг
радиуса R, т.е. круг, радиус которого равен радиусу шара. Такой круг называется большим кругом шара
Слайд 7
O
d
C (0;0;d)
α
y
x
z
d = R
Тогда R2 – d2 =0
Следовательно, точка О
– единственная общая точка сферы и плоскости.
Если расстояние от центра
сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.2
Слайд 8
α
y
x
d
z
C (0;0;d)
O
3
d > R
Тогда R2 – d2 < 0 ,
и уравнению не удовлетворяют координаты никакой точки.
Если расстояние от центра
сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.
Слайд 9
α
О
А
Касательная плоскость к сфере
Плоскость, имеющая со сферой только одну общую
точку, называется касательной плоскостью сферы.
Их общая точка называется точкой касания
плоскости и сферы. Теорема1:Радиус сферы, проведён- ный в точку касания сферы и плоскости, перпендикулярен касательной плоскости.
Теорема2: Если радиус сферы перпендикулярен к плоскости, проходящий через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
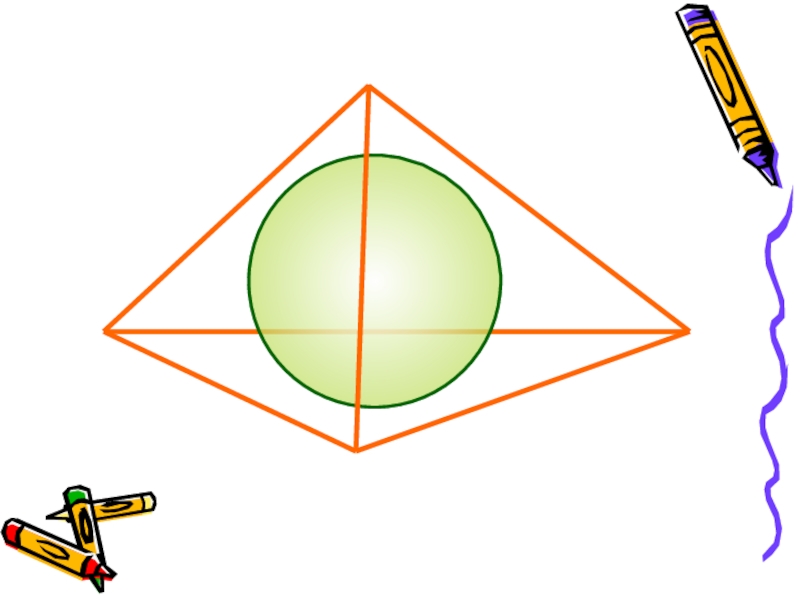
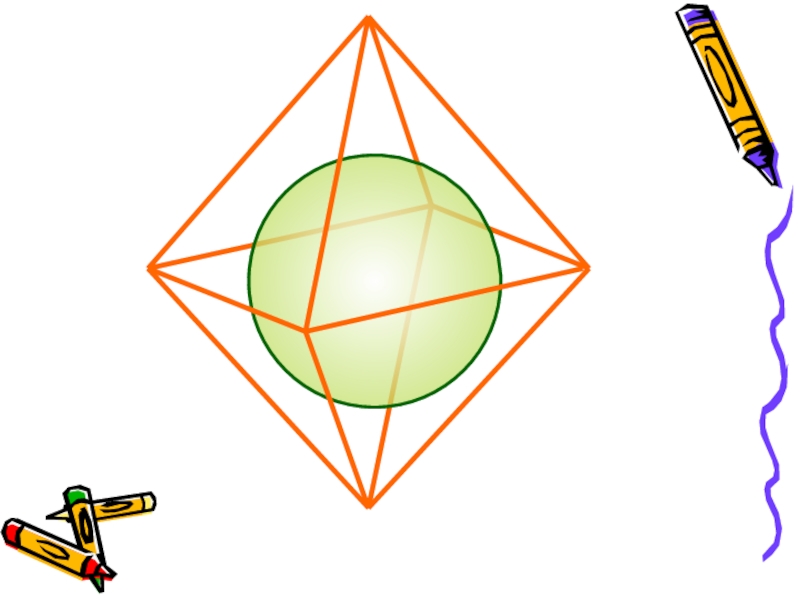
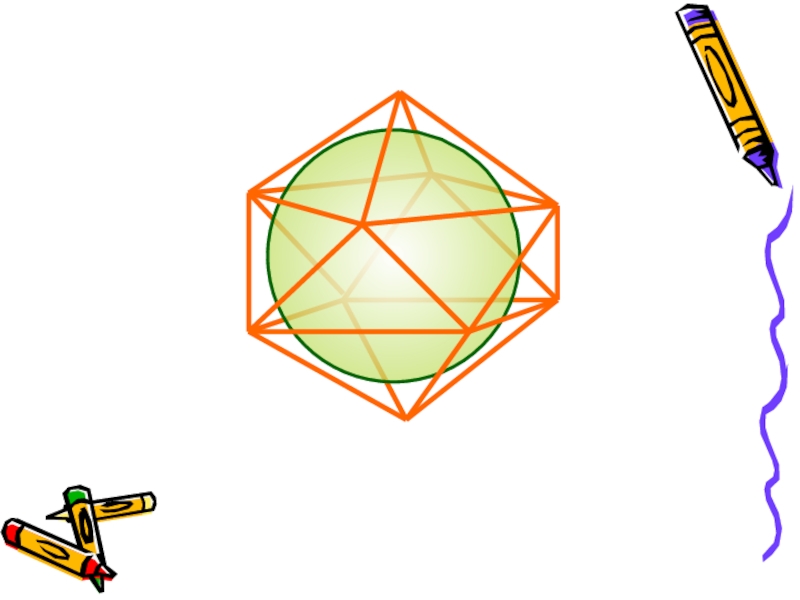
Слайд 10За площадь сферы примем предел последовательности площадей поверхностей описанных около
сферы многогранников при стремлении к нулю наибольшего размера каждой грани.
Получим
формулу для вычисления площади сферы радиуса R:S = 4 π R2
ПЛОЩАДЬ СФЕРЫ
Слайд 14
B
O
R
r
x
M
A
x
С
ОБЪЁМ ШАРА
Рассмотрим шар радиуса R и центром в точке О
и
выберем ось Ох произвольным образом
Сечение шара плоскостью, перпендикулярной к оси
Ох и проходящие через точку М на этой оси, является кругом с центром в точке М.Из прямоугольного треугольника ОМС находим
Применяя основную формулу для вычисления объёмов, получим
Так как S(x) = πr2 , то S(x) = π (R2 - x2)
Слайд 15
С
О
В
α
х
АВ = h
А
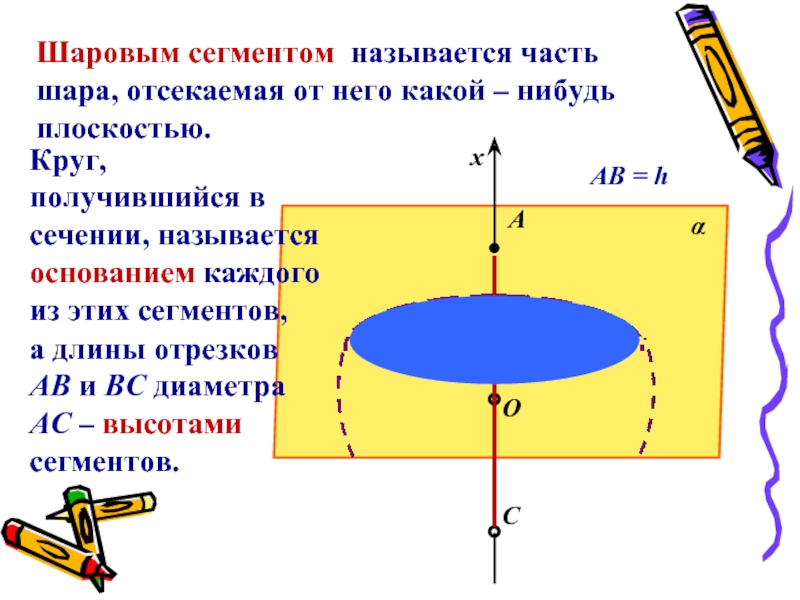
Шаровым сегментом называется часть шара, отсекаемая от него
какой – нибудь плоскостью.
Круг, получившийся в сечении, называется основанием каждого
из этих сегментов,а длины отрезков АВ и ВС диаметра АС – высотами сегментов.
Слайд 16
шаровой
слой
С
В
А
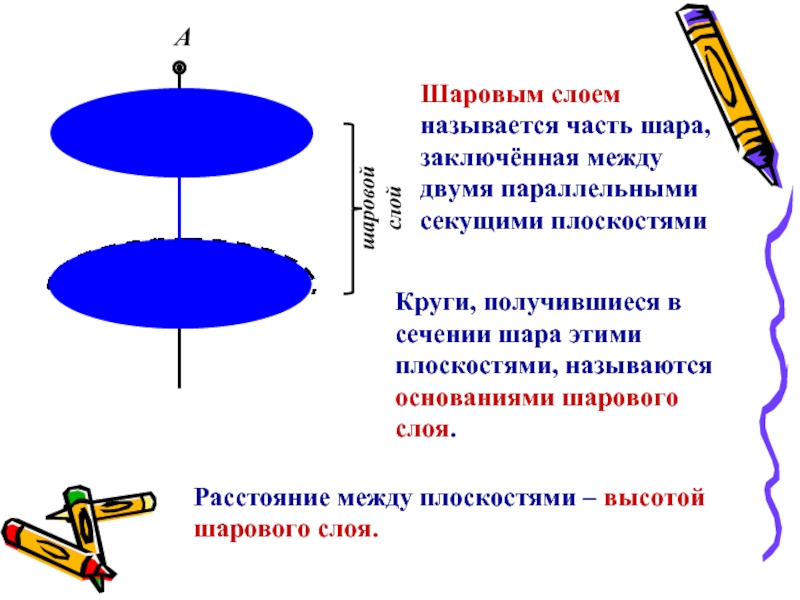
Шаровым слоем называется часть шара, заключённая между двумя параллельными секущими
плоскостями
Круги, получившиеся в сечении шара этими плоскостями, называются основаниями шарового
слоя.Расстояние между плоскостями – высотой шарового слоя.
Слайд 17
конус
шаровой
сегмент
O
r
R
Шаровым сектором называется тело, полученное вращением кругового сектора с углом,
меньшим 90°, вокруг прямой, содержащей один из ограничивающих сектор радиусов.
Шаровой
сектор состоит из шарового сегмента и конуса
Теги
