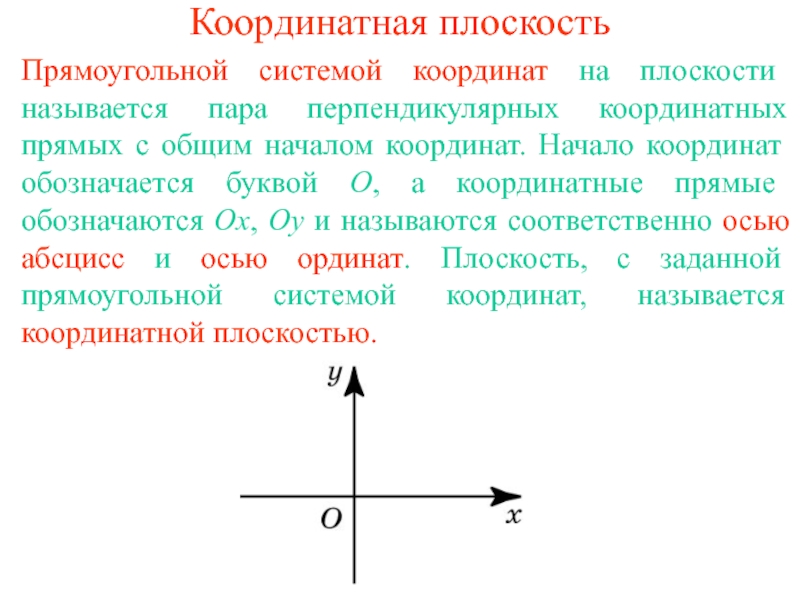
выбраны точка O, называемая началом координат, и единичный отрезок OE,
указывающий положительное направление координатной прямой.Координатой точки А на координатной прямой называется расстояние x от точки А до начала координат О, взятое со знаком "+", если А принадлежит положительной полуоси, и со знаком "–", если А принадлежит отрицательной полуоси.
Теорема. Расстояние между точками А1, А2 на координатной прямой с координатами x1, x2 соответственно выражается формулой: А1А2 = |x1 - x2|.