Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение в пространстве 10 класс
Содержание
- 1. Движение в пространстве 10 класс
- 2. 1. Центральная симметрия
- 3. Движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.
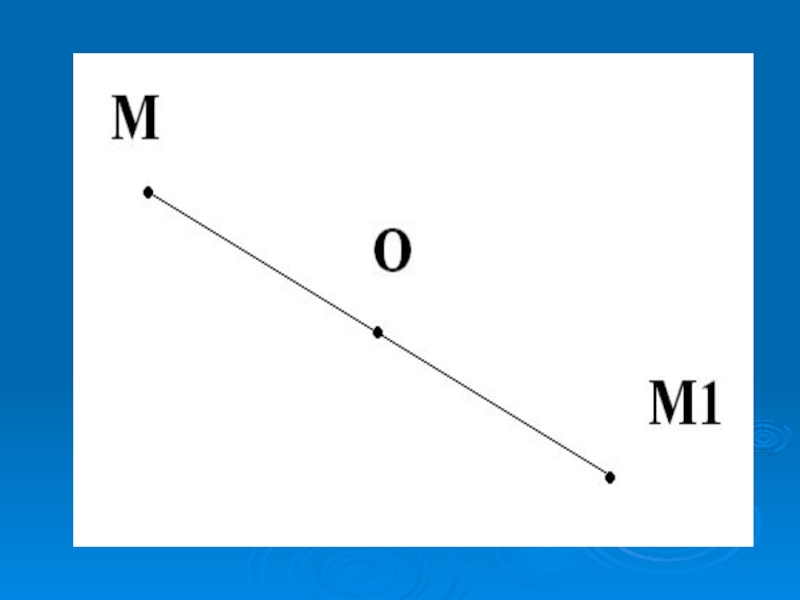
- 4. Центральная симметрия – отображение пространства на себя,
- 5. Слайд 5
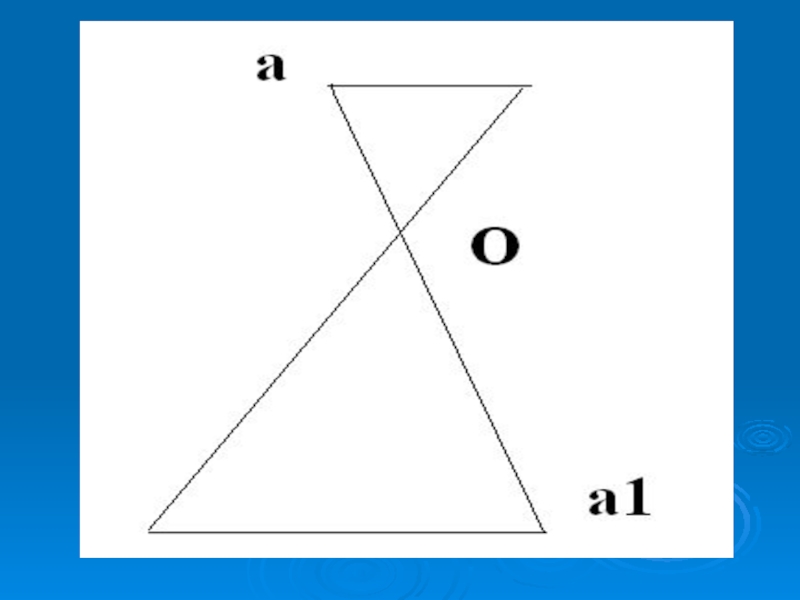
- 6. 2. Осевая симметрия
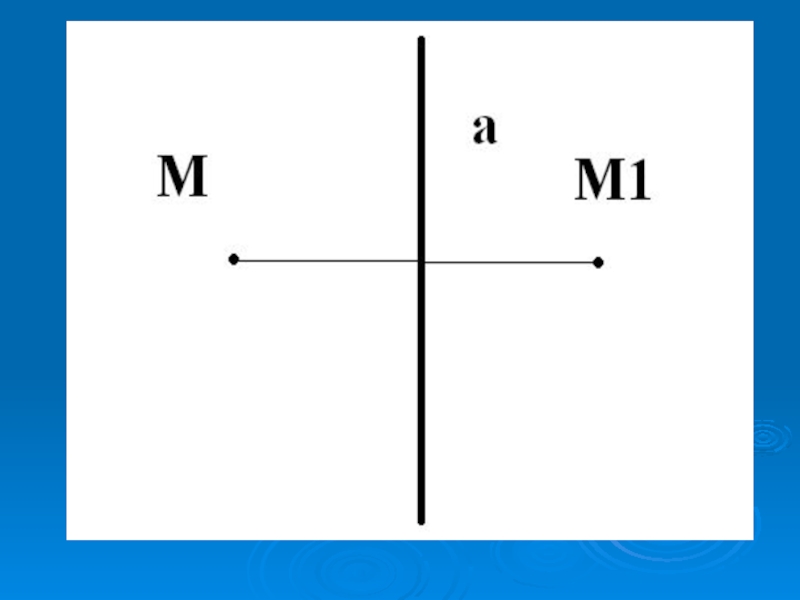
- 7. Осевой симметрией с осью а называется такое
- 8. Слайд 8
- 9. 3. Зеркальная симметрия
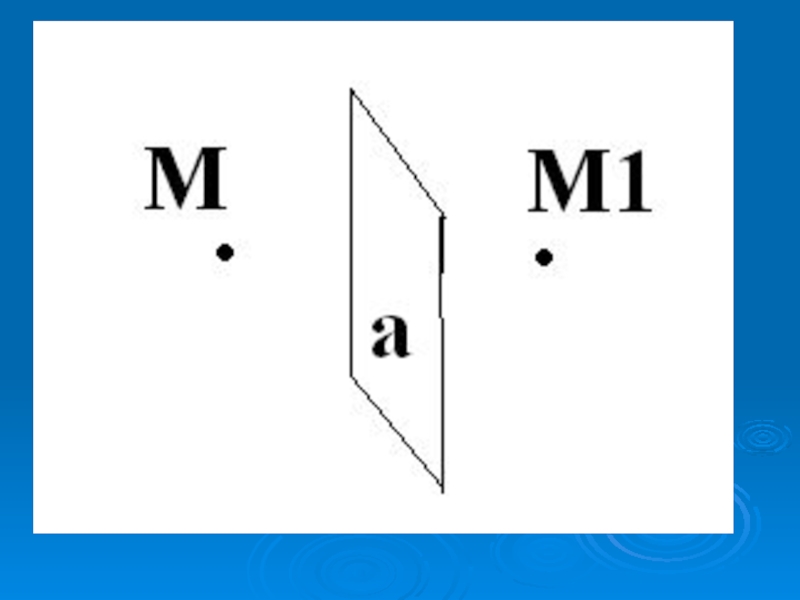
- 10. Зеркальной симметрией (симметрией относительно плоскости α) называется
- 11. Слайд 11
- 12. 4. Параллельный перенос
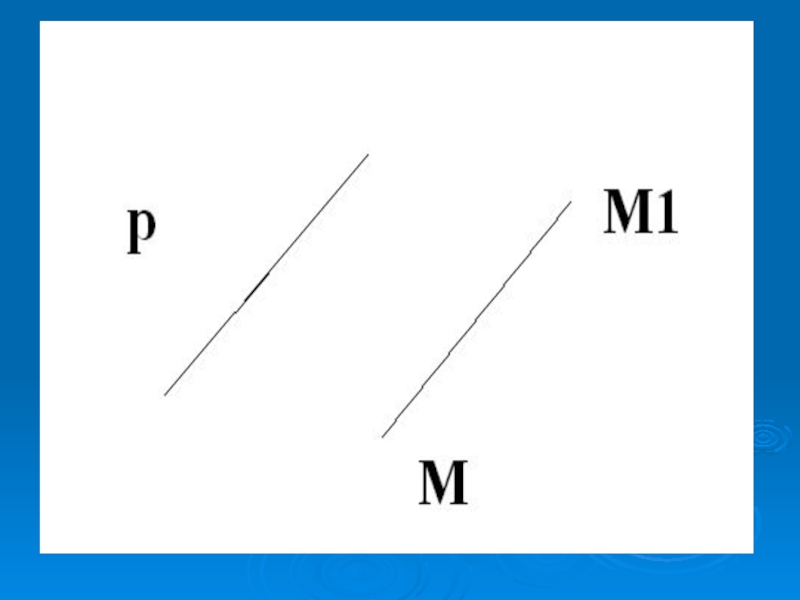
- 13. Параллельным переносом на вектор р называется отображение
- 14. Слайд 14
- 15. 5. Преобразование подобия
- 16. Центральным подобием с центром О и коэффициентом
- 17. Слайд 17
- 18. Скачать презентанцию
1. Центральная симметрия
Слайды и текст этой презентации
Слайд 3Движение пространства – это отображение пространства на себя, сохраняющее расстояние
между точками.
Слайд 4Центральная симметрия – отображение пространства на себя, при котором любая
точка М переходит в симметричную ей точку М1 относительно данного
центра О.
Слайд 7Осевой симметрией с осью а называется такое отображение пространства на
себя, при котором любая точка М переходит в симметричную ей
точку М1 относительно оси а.
Слайд 10Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства
на себя, при котором любая точка М переходит в симметричную
ей относительно плоскости α точку М1
Слайд 13Параллельным переносом на вектор р называется отображение пространства на себя,
при котором любая точка М переходит в такую точку М1,
что ММ1= р
Слайд 16Центральным подобием с центром О и коэффициентом k≠0 называется отображение
пространства на себя, при котором каждая точка М переходит в
такую точку М1, что ОМ1=kОМ
