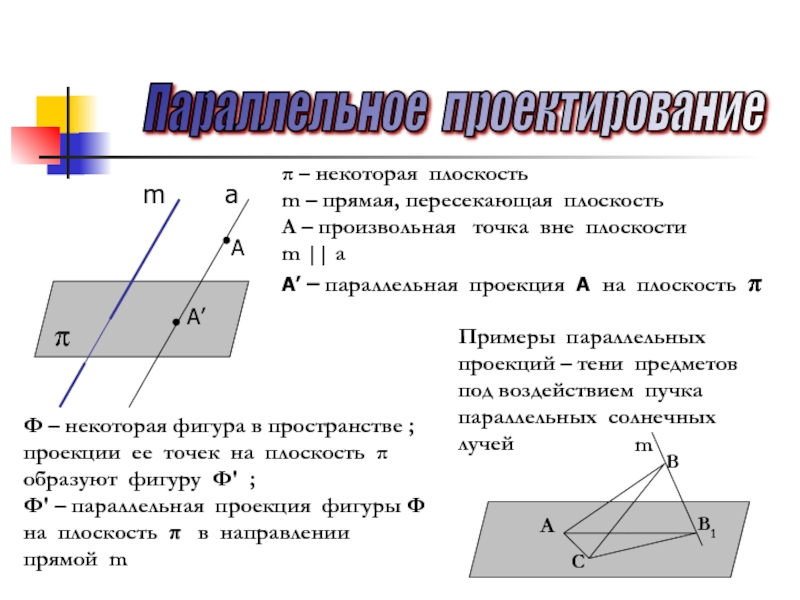
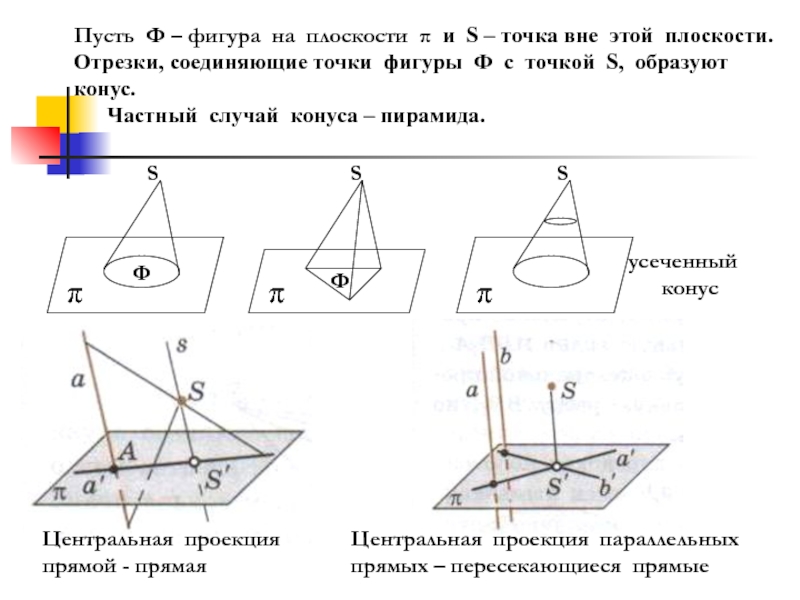
– произвольная точка вне плоскости
m || а
А’ – параллельная
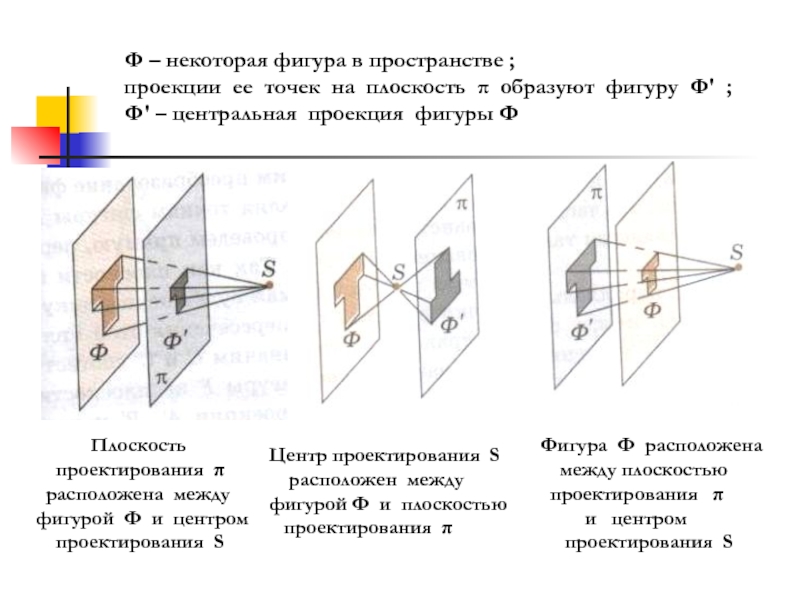
проекция А на плоскость πФ – некоторая фигура в пространстве ;
проекции ее точек на плоскость π
образуют фигуру Ф' ;
Ф' – параллельная проекция фигуры Ф
на плоскость π в направлении
прямой m
Примеры параллельных проекций – тени предметов под воздействием пучка
параллельных солнечных
лучей
А
С
В
В1
m