К уроку геометрии в 8 классе "Признаки параллелограмма"

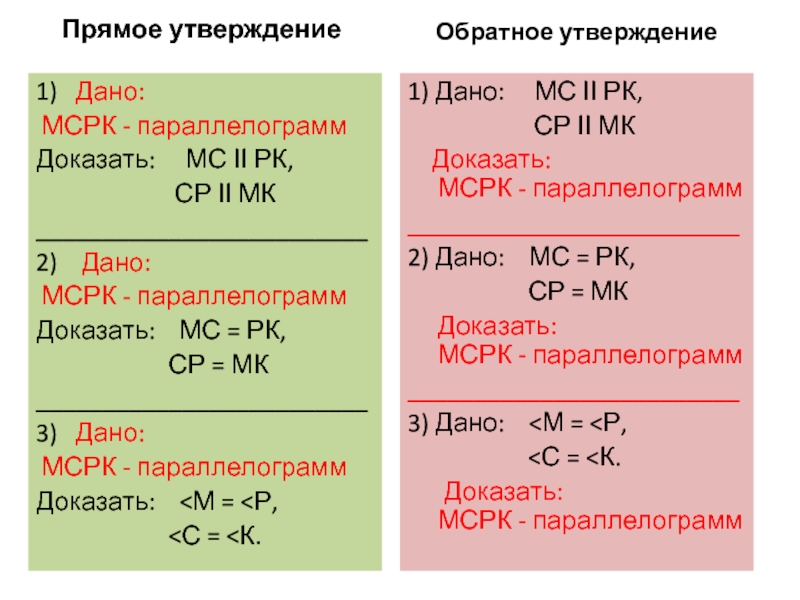
ІІ РК,

Обратное утверждение

1) Дано: МС ІІ РК,
СР ІІ МК
Доказать: МСРК - параллелограмм
_________________________
2) Дано: МС = РК,
СР = МК
Доказать: МСРК - параллелограмм
_________________________
3) Дано: <М = <Р,
<С = <К.
Доказать: МСРК - параллелограмм

Прямое утверждение

составляют
180°


Равны соответствующие треугольники

Имеются треугольники, в которых есть 3 пары соответственно

BC

Доказать: ABCD - параллелограмм

1) AB = CD (по условию),
BC = AD (по условию),
AC – общая,
следовательно, ∆ ABC = ∆ ACD,
следовательно < 1 = < 2, < 3 = < 4.
2) < 1 = < 2, они накрест лежащие,
следовательно, BC ǁ AD.
3) < 3 = < 4, они накрест лежащие,
следовательно, AB ǁ CD.
4) Получили BC ǁ AD ,
AB ǁ CD,
следовательно , ABCD – параллелограмм,
что и требовалось доказать.

AB

Доказать: ABCD - параллелограмм

1) AB ǁ CD,
следовательно, < 3 = < 4 ( они – накрест лежащие при пересечении прямых AB и CD секущей AC).
2) AB = CD (по условию),
< 3 = < 4 (доказали),
AC – общая,
следовательно, ∆ ABC = ∆ ACD,
следовательно BC = AD.
3) Получили
BC = AD (доказали),
AB = CD (по условию),
следовательно , ABCD – параллелограмм,
что и требовалось доказать.

- параллелограмм.