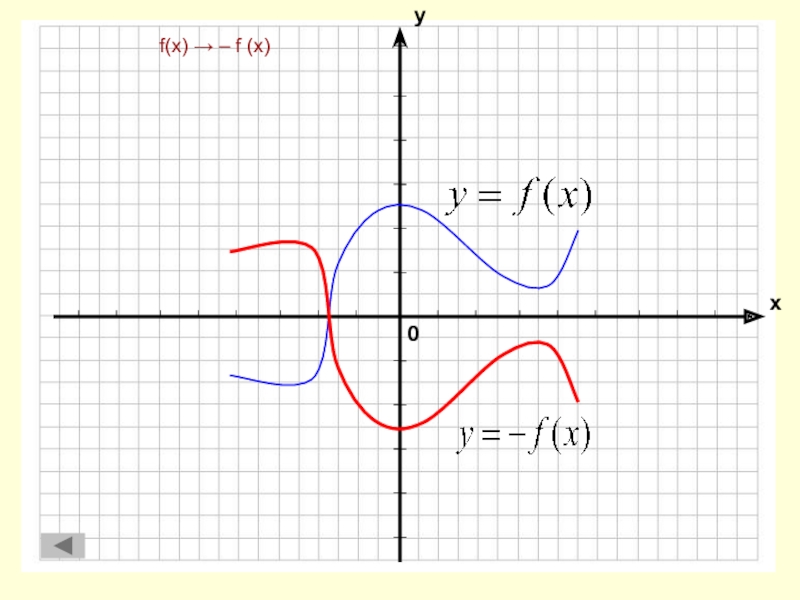
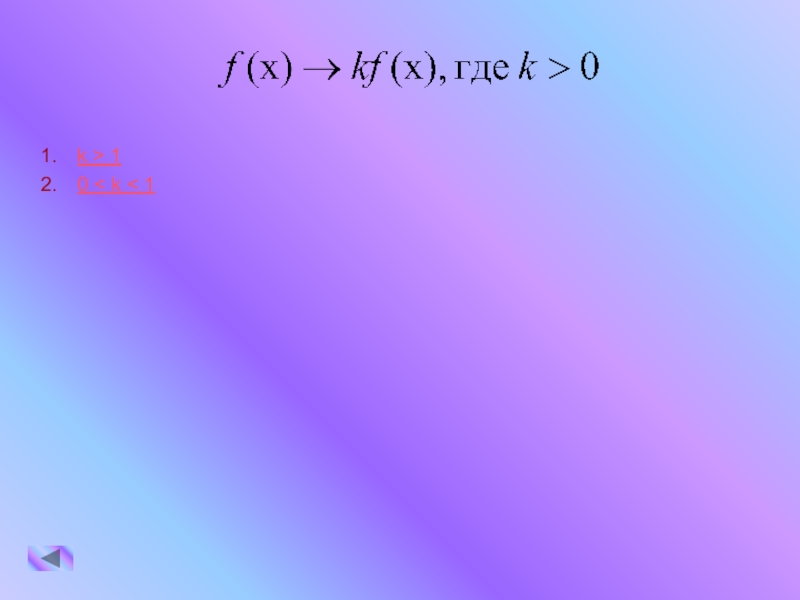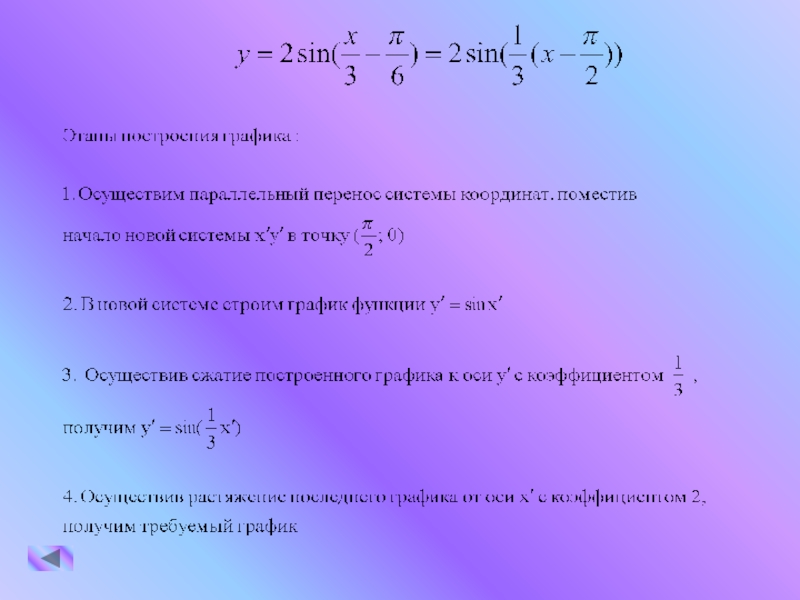оси ординат
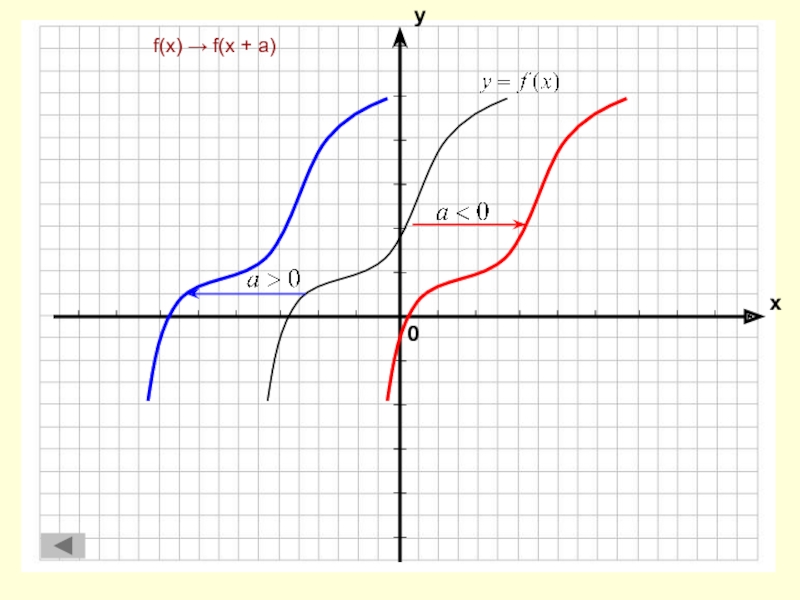
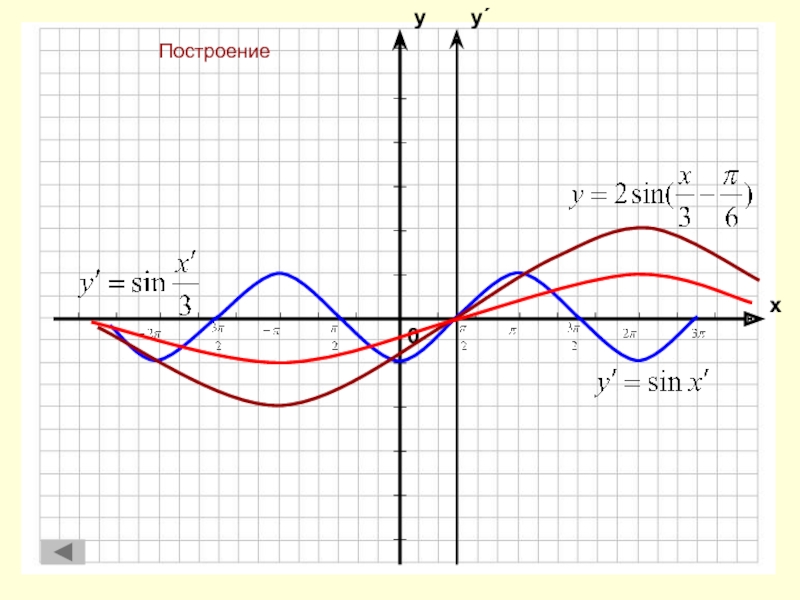
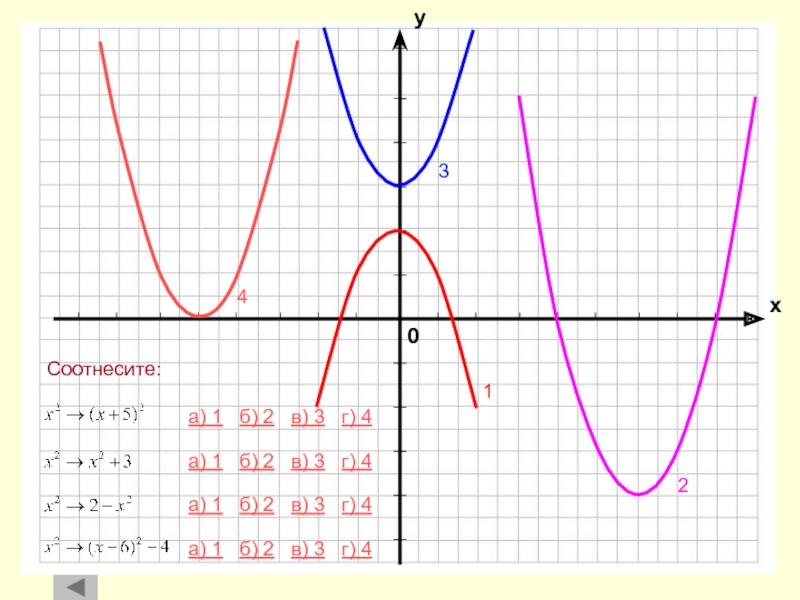
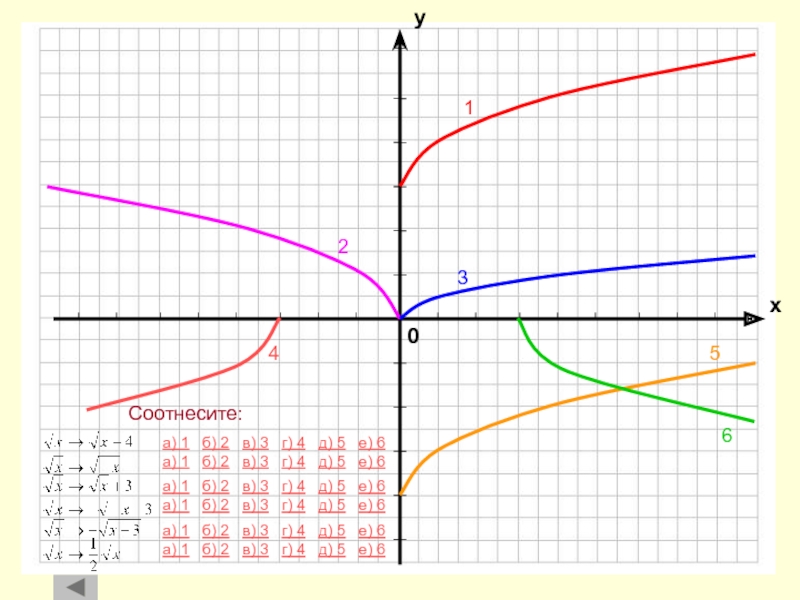
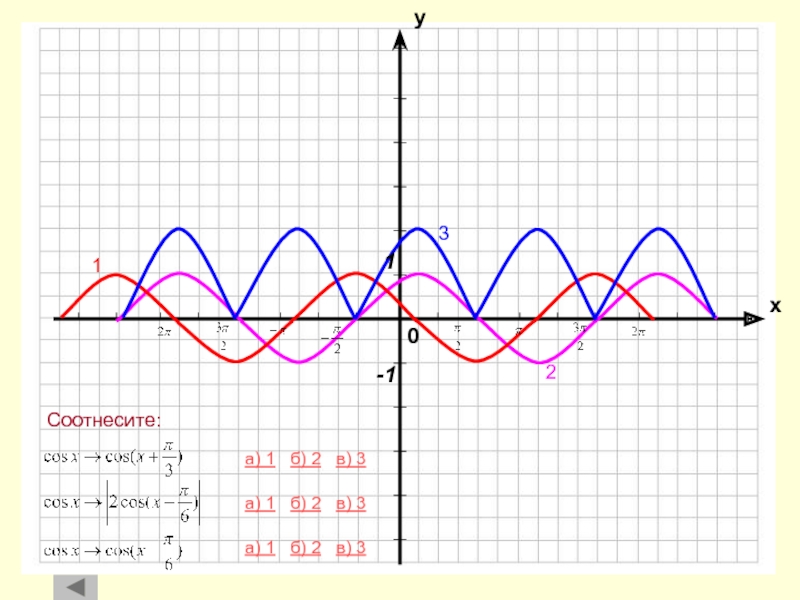
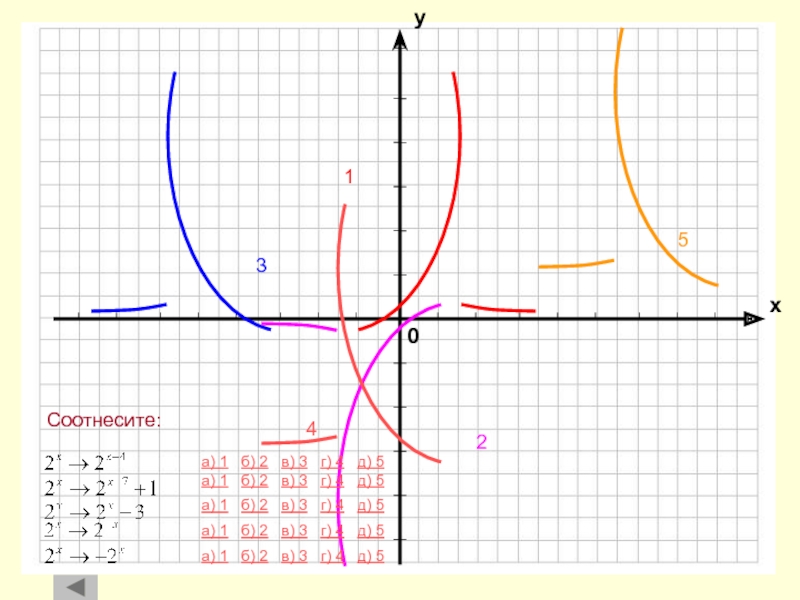
Параллельный перенос вдоль оси абсцисс
Параллельный перенос вдоль оси ординат
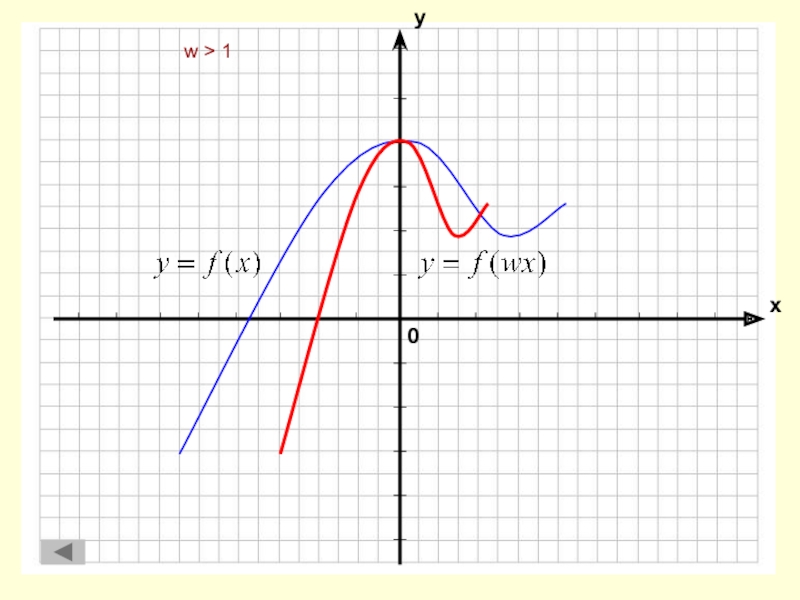
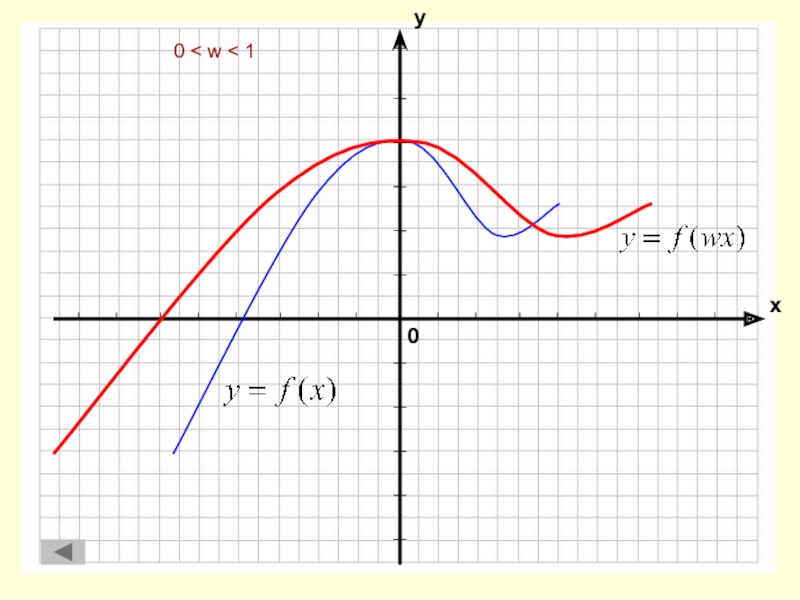
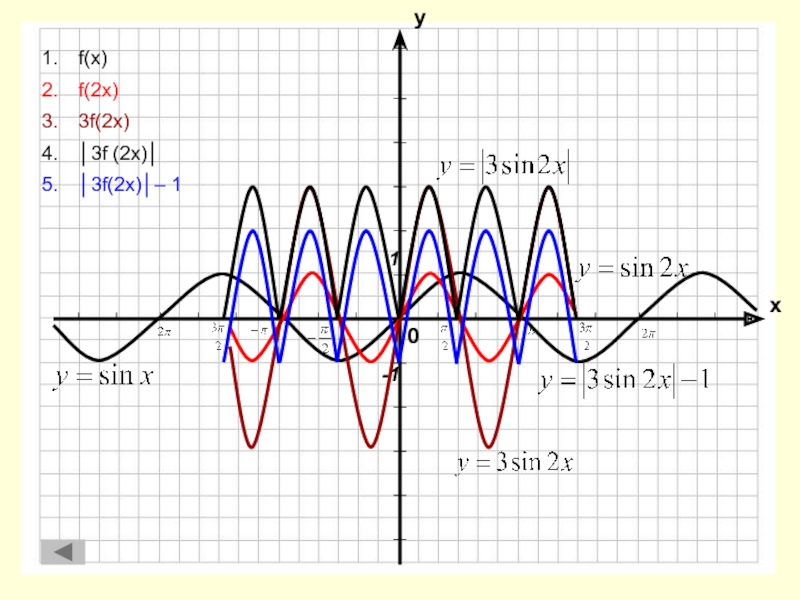
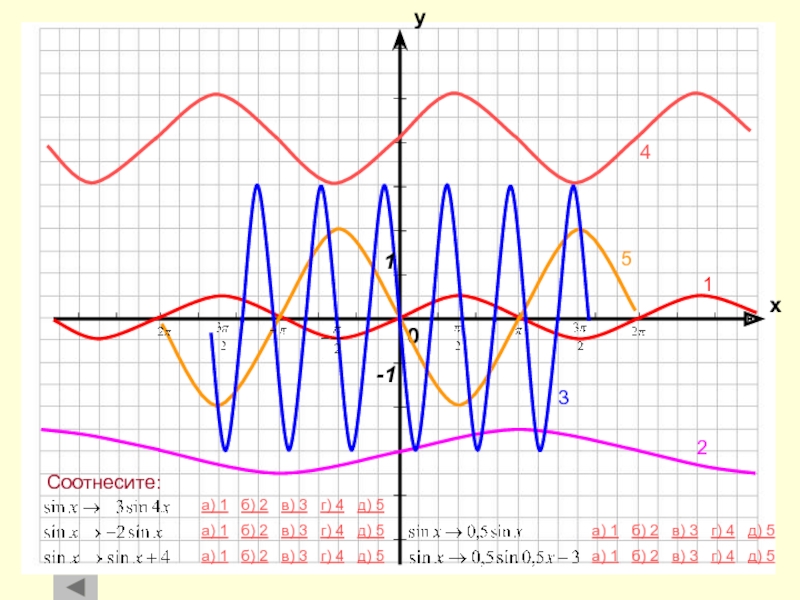
Растяжение
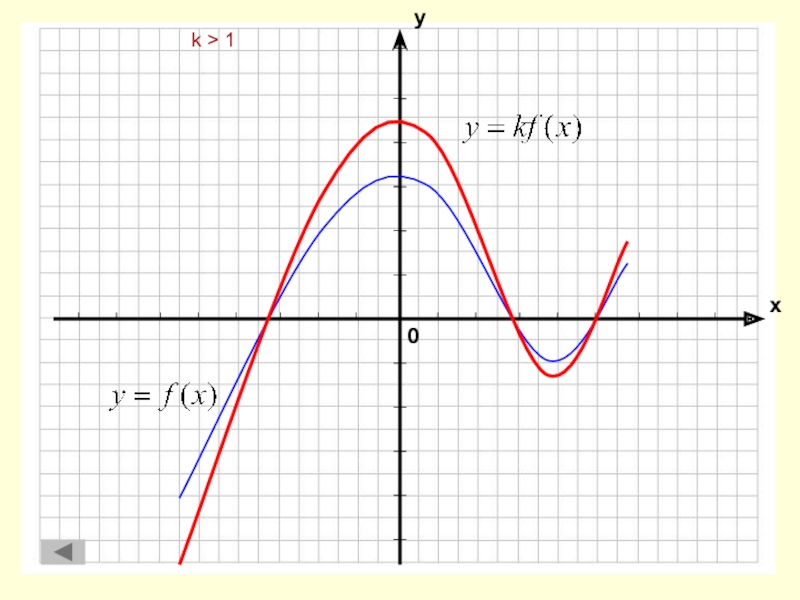
и сжатие вдоль оси абсциссРастяжение и сжатие вдоль оси ординат
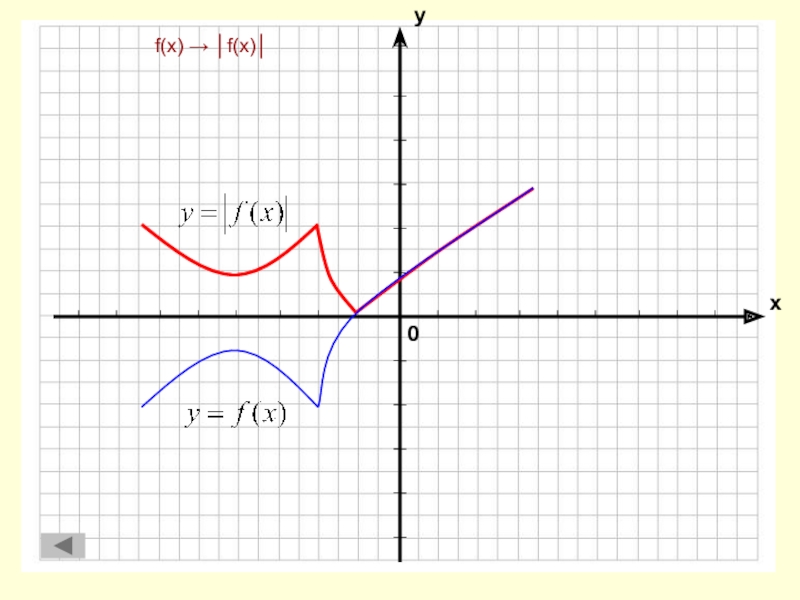
Построение графика функции у =│f(x)│
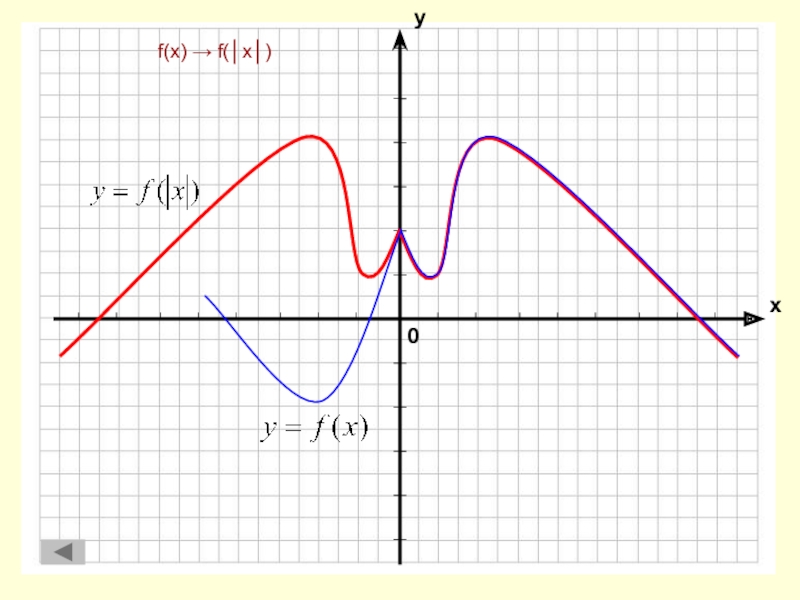
Построение графика функции у = f(│x│)
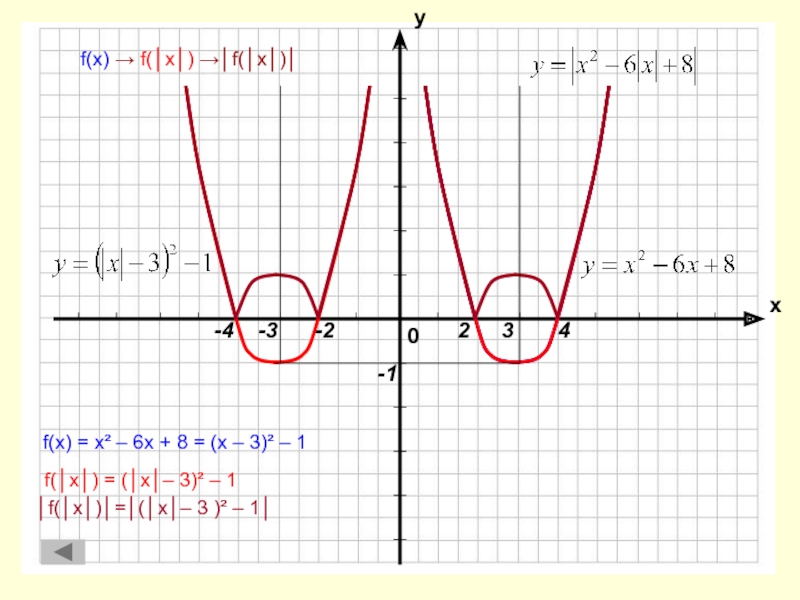
Построение графика функции у = │f(│x│)│
Содержание