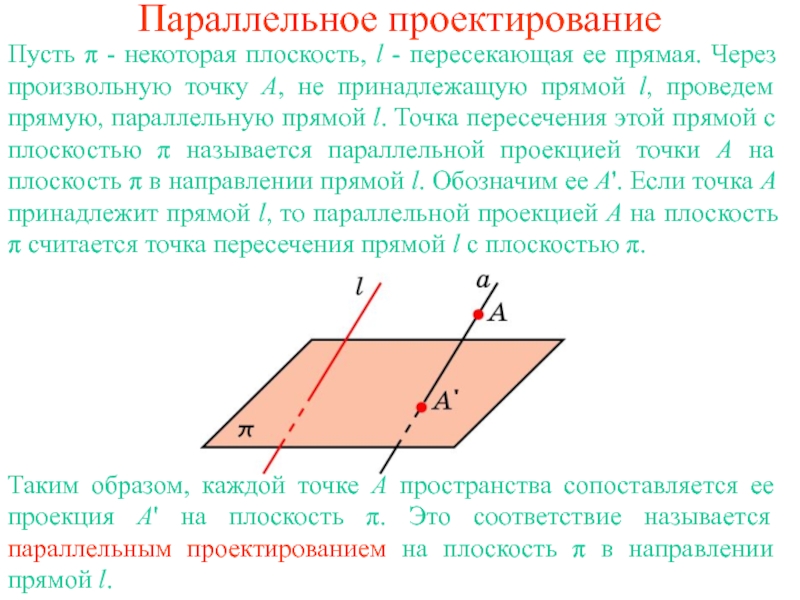
A' на плоскость π. Это соответствие называется параллельным проектированием на
плоскость π в направлении прямой l.Пусть π - некоторая плоскость, l - пересекающая ее прямая. Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью π называется параллельной проекцией точки A на плоскость π в направлении прямой l. Обозначим ее A'. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость π считается точка пересечения прямой l с плоскостью π.