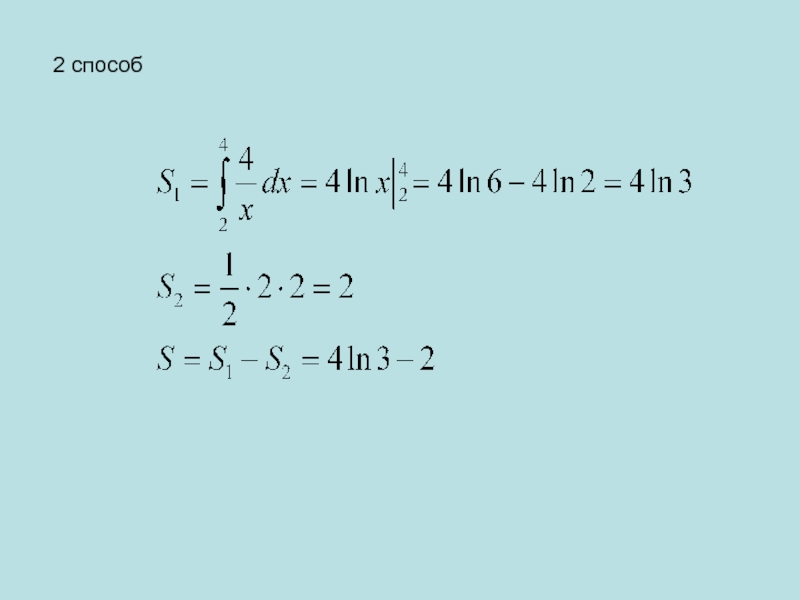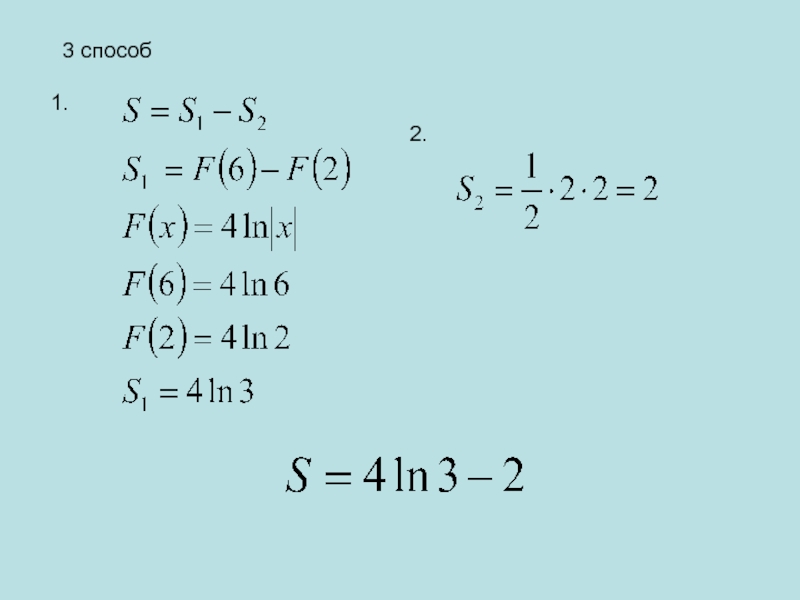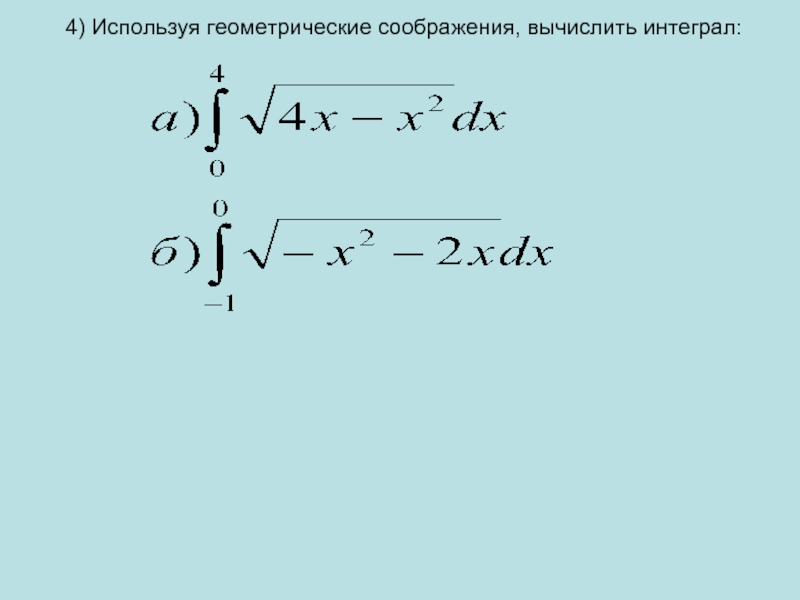Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площадь криволинейной трапеции
Содержание
- 1. Площадь криволинейной трапеции
- 2. Площадь криволинейной трапеции yxBCDAabY = f(x)sABCD –криволинейная трапецияS = F(b) – F(a)F/ (x) = f(x)
- 3. Y=g(x)xbayЗаписать формулу для вычисления площади криволинейной трапецииа) S = F(b) – F(a)b)
- 4. xy а
- 5. xabyY=f(x)Y=g(x)Записать формулу для вычисления площади криволинейной трапеции
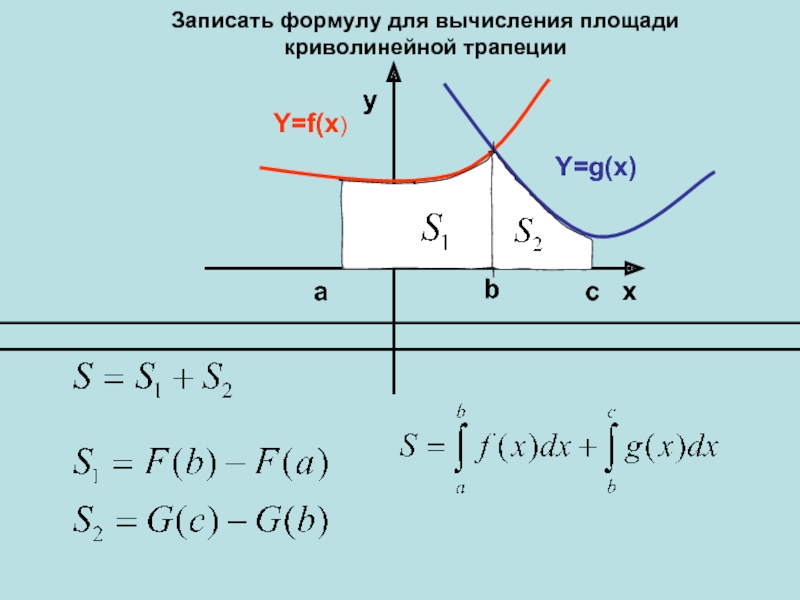
- 6. Y=f(x)Y=g(x)xyabcЗаписать формулу для вычисления площади криволинейной трапеции
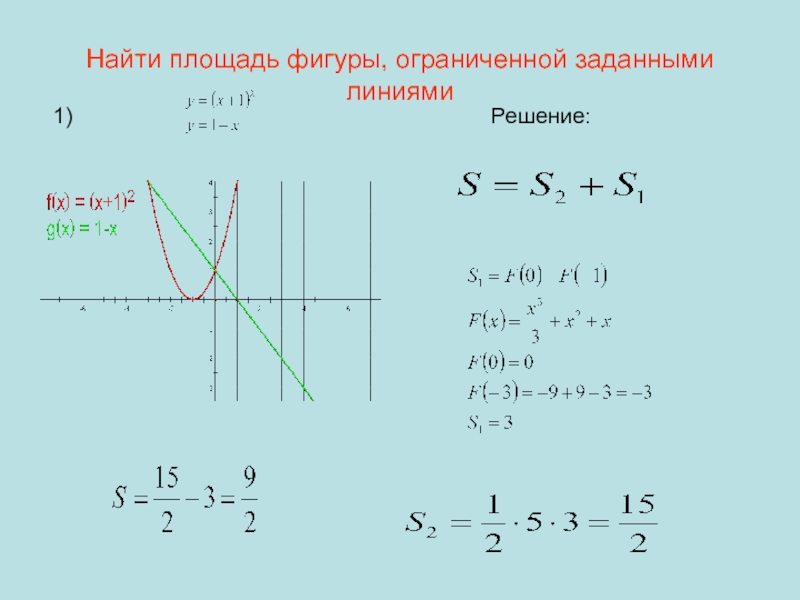
- 7. Найти площадь фигуры, ограниченной заданными линиями1) Решение:
- 8. 2)Решение:
- 9. Решение
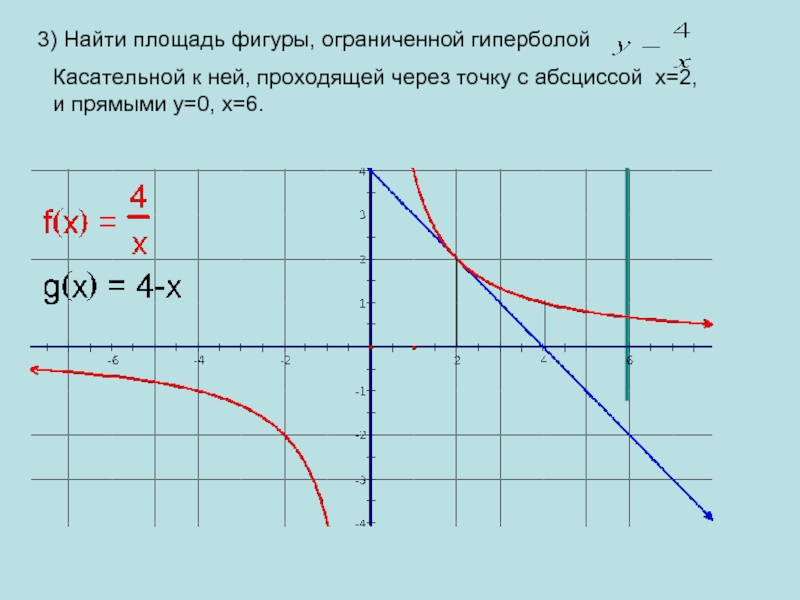
- 10. 3) Найти площадь фигуры, ограниченной гиперболой Касательной
- 11. способ:
- 12. 2 способ
- 13. 3 способ1.2.
- 14. 4) Используя геометрические соображения, вычислить интеграл:
- 15. Решение. а) Имеем: Это уравнение окружности радиуса
- 16. 5) Вычислить интеграл:
- 17. а) Фигура, площадь которой выражается заданным интегралом,
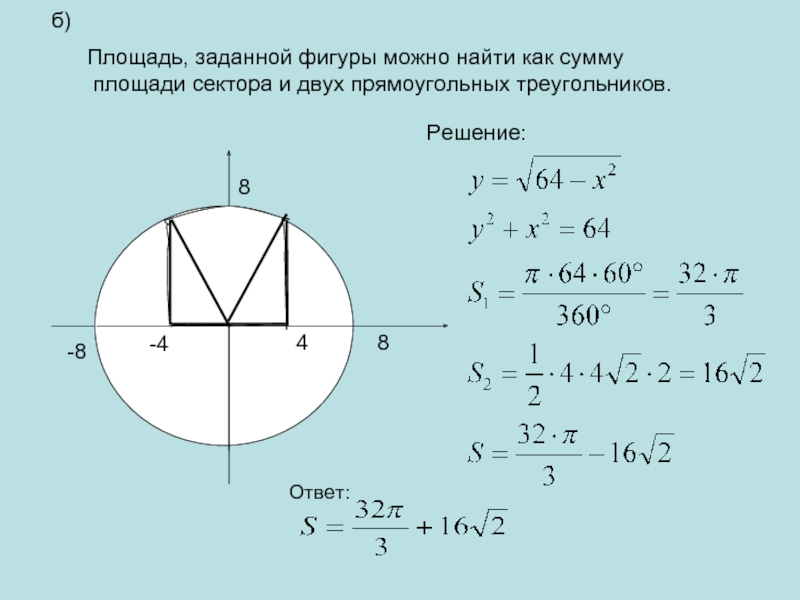
- 18. б)Площадь, заданной фигуры можно найти как сумму площади сектора и двух прямоугольных треугольников.Решение:Ответ:
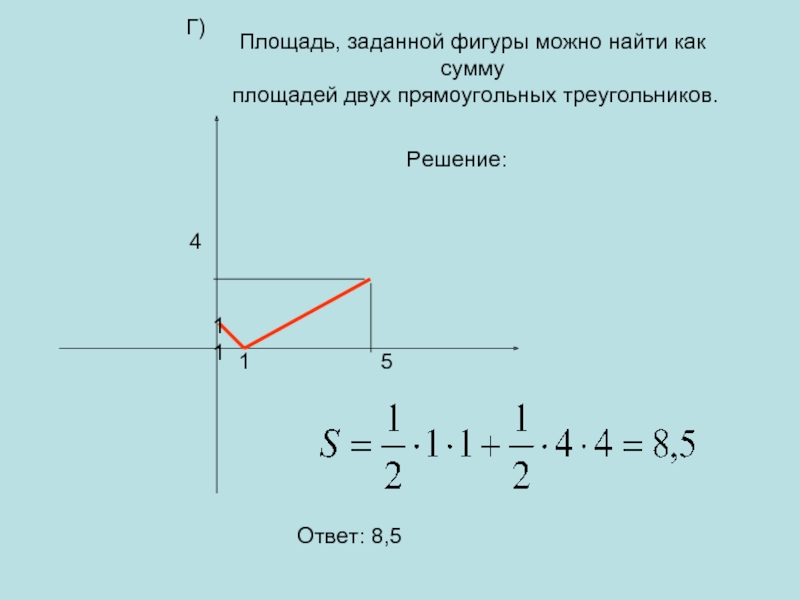
- 19. 11Площадь, заданной фигуры можно найти как сумму площадей двух прямоугольных треугольников.Г)Решение:Ответ: 8,5154
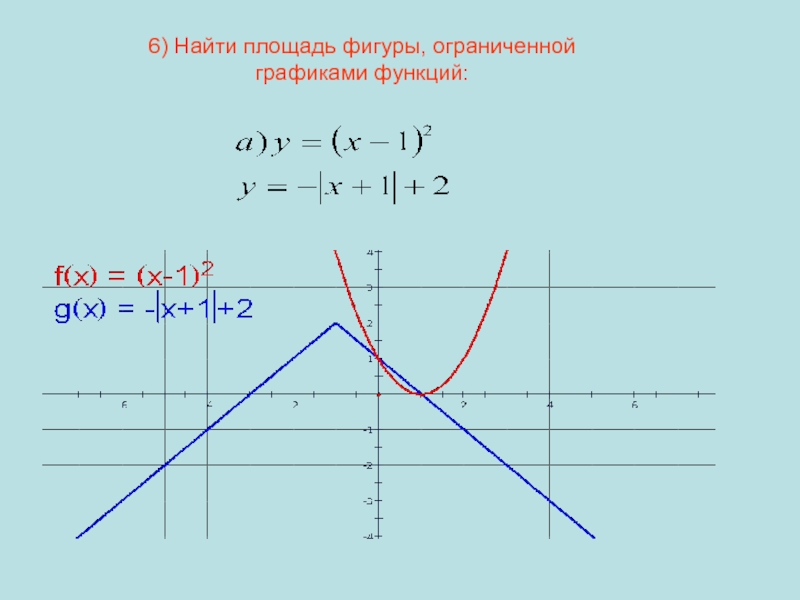
- 20. 6) Найти площадь фигуры, ограниченнойграфиками функций:
- 21. Решение:7) Найти площадь фигуры,ограниченной графикомфункции и касательной
- 22. Слайд 22
- 23. Скачать презентанцию
Площадь криволинейной трапеции yxBCDAabY = f(x)sABCD –криволинейная трапецияS = F(b) – F(a)F/ (x) = f(x)
Слайды и текст этой презентации
Слайд 4
x
y
а
b
Y= f(x)
a) S = - (F(b) –F(a)
Записать формулу для вычисления площади криволинейной трапеции
Слайд 10
3) Найти площадь фигуры, ограниченной гиперболой
Касательной к ней, проходящей
через точку с абсциссой х=2,
и прямыми у=0, х=6.
Слайд 15Решение. а) Имеем:
Это уравнение окружности радиуса r=2 с центром
в точке (2;0).
Значит, заданным интегралом выражается площадь половины круга.
б) Имеем:
Слайд 17а) Фигура, площадь которой выражается заданным интегралом,
состоит из сектора
круга радиусом 2 и центральным углом
И прямоугольного равнобедренного треугольника
с катетом Решение:
а) Уравнение окружности:
б)Найдем площадь сектора:
в) Найдем площадь треугольника:
г) Найдем площадь, заданной фигуры:
Слайд 18
б)
Площадь, заданной фигуры можно найти как сумму
площади сектора и
двух прямоугольных треугольников.
Решение:
Ответ:
Слайд 1911
Площадь, заданной фигуры можно найти как сумму
площадей двух прямоугольных
треугольников.
Г)
Решение:
Ответ: 8,5
1
5
4
Слайд 21Решение:
7)
Найти площадь фигуры,
ограниченной графиком
функции и касательной
к нему в
точке х=3
Заданная функция имеет точку максимума (1;5) и точку минимума
(3;1).Построим
график этой функции. Касательная к нему в точке х=3 параллельна оси абсцисс и имеет с графиком еще одну
общую точку (0;1).
Теги