Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площади 8 класс
Содержание
- 1. Площади 8 класс
- 2. Является утверждение верным или неверным? 1) Если два многоугольника имеют равные площади, то они равны
- 3. Является утверждение верным или неверным ?
- 4. Является утверждение верным или неверным ?3)Квадратный сантиметр – это фигура, стороны которой равны 1см
- 5. Является утверждение верным или неверным ?4) Площадь квадрата равна произведению его сторон
- 6. Является утверждение верным или неверным ?5)Площадь
- 7. Является утверждение верным или неверным ? 6) Площадь параллелограмма равна произведению стороны параллелограмма на высоту
- 8. Является утверждение верным или неверным?7) Площадь прямоугольного треугольника равна половине произведения катетов
- 9. Является утверждение верным или неверным ?8) Площадь трапеции равна произведению суммы оснований на половину высоты
- 10. Является утверждение верным или неверным ?9)
- 11. Является утверждение верным или неверным?10) Если
- 12. Выберите номер верного утверждения
- 13. 11) Высотой трапеции называется:перпендикуляр, проведённый к её
- 14. 12) Если высоты треугольников равны, то:их площади
- 15. 13) Египетским треугольником называют такой треугольник, длины
- 16. 14) Если в треугольнике АВС1) угол В
- 17. Устные геометрические задачи
- 18. Решите задачи №1abcОтвет
- 19. aabЗадача № 2Ответ : 10 Ответ поясните
- 20. Задача № 3Ответ : 36 Ответ поясните
- 21. АВСЗадача № 440º?Ответ : 50º Ответ поясните
- 22. АВС45ºЗадача № 5 Ответ : 8 Ответ поясните
- 23. 10152530º
- 24. Задача № 7АВСDОтвет : 5
- 25. КDАВС352Задача № 8Ответ : 10Ответ поясните
- 26. АВСDЗадача № 9Ответ : 96 Ответ поясните
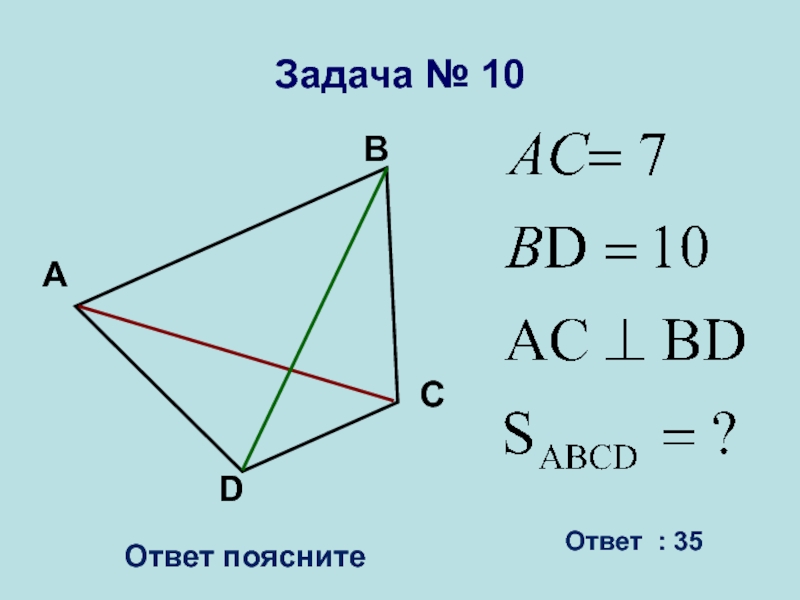
- 27. АВСDЗадача № 10Ответ поясните Ответ : 35
- 28. КDАВС5437Задача № 11Ответ : 42
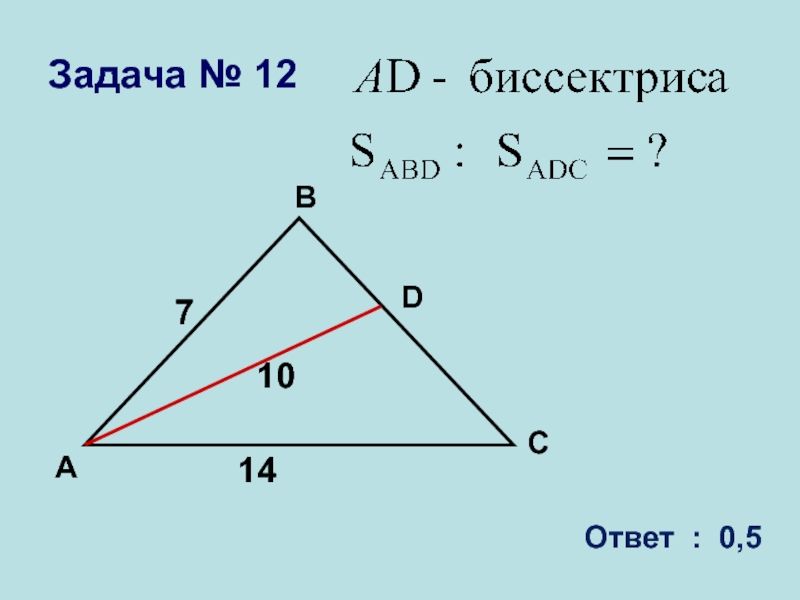
- 29. DАВС14107Задача № 12Ответ : 0,5
- 30. Задача – исследование: Вывести Формулу площади равностороннего треугольникаАВС
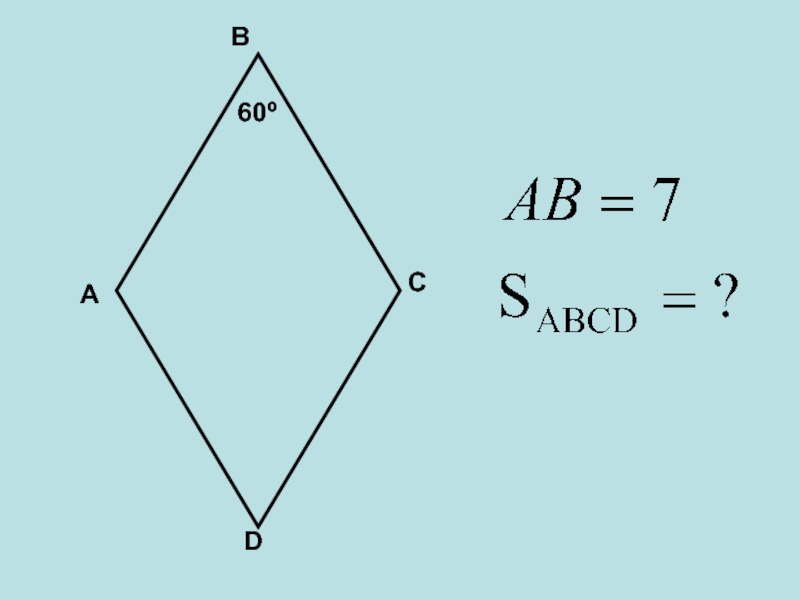
- 31. АВСD60º
- 32. Скачать презентанцию
Является утверждение верным или неверным? 1) Если два многоугольника имеют равные площади, то они равны
Слайды и текст этой презентации
Слайд 2Является утверждение верным или неверным?
1) Если два многоугольника
имеют равные площади, то они равны
Слайд 3Является утверждение
верным или неверным ?
2) Если многоугольник
составлен из нескольких многоугольников, то его площадь равна сумме площадей
этих многоугольниковСлайд 4Является утверждение
верным или неверным ?
3)Квадратный сантиметр – это фигура,
стороны которой равны 1см
Слайд 6Является утверждение
верным или неверным ?
5)Площадь треугольника равна произведению стороны
на высоту, проведённую к этой стороне
Слайд 7Является утверждение
верным или неверным ?
6) Площадь параллелограмма равна
произведению стороны параллелограмма на высоту
Слайд 8Является утверждение
верным или неверным?
7) Площадь прямоугольного треугольника равна половине
произведения катетов
Слайд 9Является утверждение
верным или неверным ?
8) Площадь трапеции равна произведению
суммы оснований на половину высоты
Слайд 10Является утверждение
верным или неверным ?
9) Теорема Пифагора гласит: Если
квадрат одной стороны треугольника равен сумме квадратов двух других сторон,
то треугольник прямоугольныйСлайд 11Является утверждение
верным или неверным?
10) Если угол одного треугольника равен
углу другого треугольника, то площади этих треугольников относятся как произведения
сторон , заключающих равные углыСлайд 1311) Высотой трапеции называется:
перпендикуляр, проведённый к её основанию
отрезок, пересекающий основание
под прямым углом
перпендикуляр, опущенный из вершины трапеции
перпендикуляр, проведенный из любой
точки одного из оснований к прямой, содержащей другое основание.Слайд 1412) Если высоты треугольников равны, то:
их площади равны
их площади относятся
как основания
эти треугольники равны
основания к которым они проведены, равны
Слайд 1513) Египетским треугольником называют такой треугольник, длины сторон которого:
удовлетворяют теореме
Пифагора
удовлетворяют, обратной теореме Пифагора
равны 3,4 и 5
равны целым числам
Слайд 16
14) Если в треугольнике АВС
1) угол В – прямой
угол С
– прямой
угол А – прямой
угол С или угол А
прямой