Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Замечательные кривые. эллипса 7 класс
Содержание
- 1. Замечательные кривые. эллипса 7 класс
- 2. Прямая и окружность – две наиболее простые
- 3. Цели урока Познакомить учащихся с определением
- 4. Ход урокаОпределение эллипсаКаноническое уравнение эллипсаПостроение эллипсаОкружность -
- 5. Определение эллипса Эллипсом
- 6. Каноническое уравнение эллипсаMF1+MF2=2a - характеристическое свойство эллипсаy0b-
- 7. Построение эллипса Задача: Изобразить в
- 8. Окружность – частный случай эллипсаУравнение эллипса хху0а
- 9. Приборы для построения эллипсаЭллиптический циркульВеревочный способММF1F2
- 10. Оптические свойства эллипса и их применениеОпыт 1
- 11. Эллипс в жизни 1
- 12. Выводы Достижение поставленной целиРезультаты деятельности учащихся на урокеПодведение итогов
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Цели урока
Познакомить учащихся с определением эллипса; рассмотреть его замечательные
свойства и их применение
Развивать логическое, творческое и абстрактное мышление,
интерес к предметуЗадача Активизация мыслительной деятельности и познавательной активности учащихся
Слайд 4Ход урока
Определение эллипса
Каноническое уравнение эллипса
Построение эллипса
Окружность - частный случай эллипса
Приборы
для построения эллипса
Оптические свойства эллипса и их применение
Эллипс в
жизниИтог урока
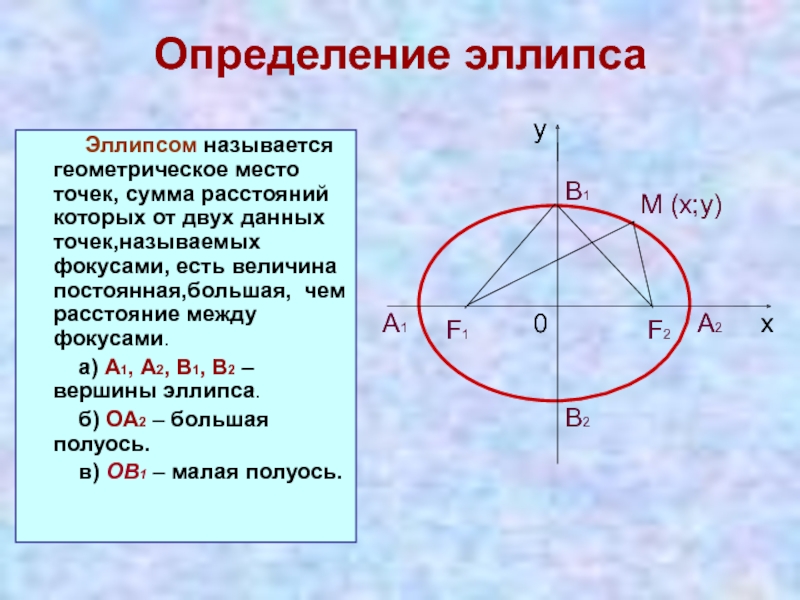
Слайд 5Определение эллипса
Эллипсом называется геометрическое место
точек, сумма расстояний которых от двух данных точек,называемых фокусами, есть
величина постоянная,большая, чем расстояние между фокусами.а) А1, А2, В1, В2 – вершины эллипса.
б) ОА2 – большая полуось.
в) ОВ1 – малая полуось.
y
x
0
B1
A1
B2
A2
F1
F2
M (x;y)
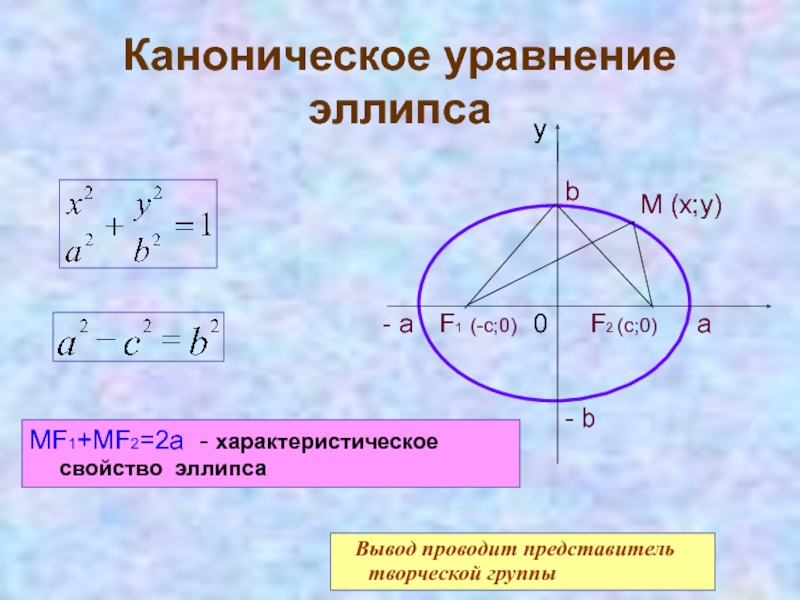
Слайд 6Каноническое уравнение эллипса
MF1+MF2=2a - характеристическое свойство эллипса
y
0
b
- а
- b
a
F1 (-c;0)
F2
(c;0)
M (x;y)
Вывод проводит представитель творческой группы
Слайд 7Построение эллипса
Задача: Изобразить в координатной плоскости эллипс,
заданный уравнением
у
х
4
5
-4
-5
0
Решение
а) а = 5,
b = 4
c =
3b) F1 (-3;0), F2(3;0)-фокусы
в) симметрия относительно оХ, оУ, и О(0;0)
Работа с классом с использованием слайда – учебная дискуссия
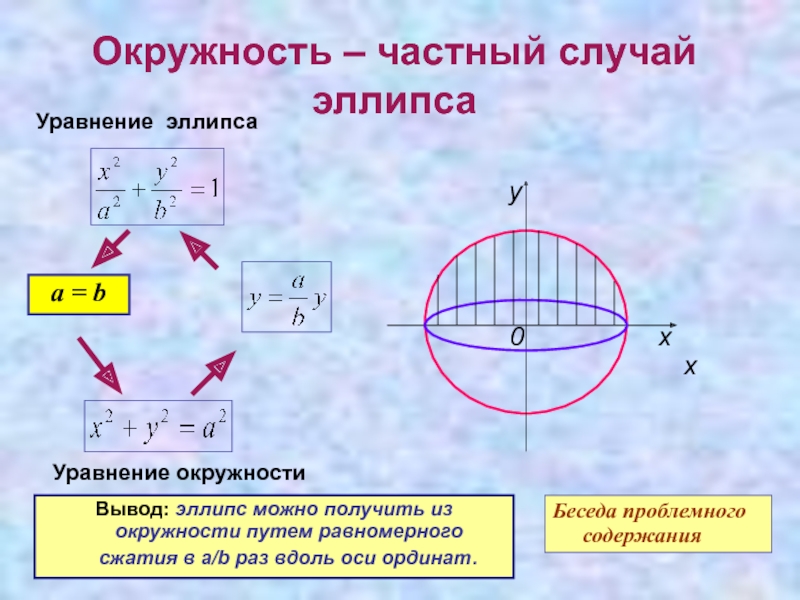
Слайд 8Окружность – частный случай эллипса
Уравнение эллипса
хх
у
0
а = b
Уравнение
окружности
Вывод: эллипс можно получить из окружности путем равномерного сжатия в
а/b раз вдоль оси ординат.Беседа проблемного содержания
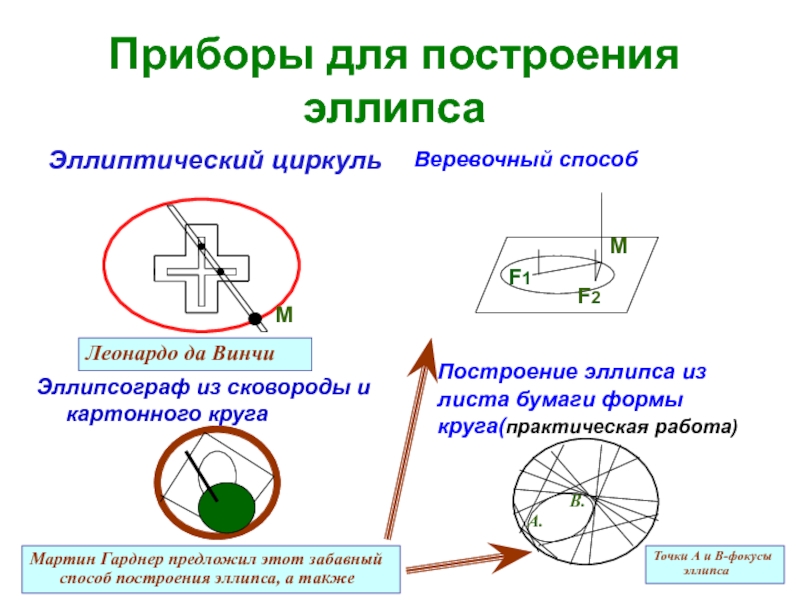
Слайд 9Приборы для построения эллипса
Эллиптический циркуль
Веревочный способ
М
М
F1
F2
Построение эллипса из
листа бумаги формы круга(практическая работа)
Эллипсограф из сковороды и картонного круга
А.
B.
Точки
А и В-фокусы эллипсаМартин Гарднер предложил этот забавный способ построения эллипса, а также
Леонардо да Винчи
Слайд 10Оптические свойства эллипса и их применение
Опыт 1 .В неглубокий эллиптический
таз налита вода.В месте первого фокуса (F1) опускают несколько раз
палец после чего расходятся круговые волны, и, отражаясь от края, сходятся в месте второго фокуса (F2), образуя лунку.Вопрос:
Почему волны сходятся в месте второго фокуса?
Использование оптического
свойства эллипса в быту
В 1964 году в США Артур Фриго придумал игру «Эллиптипул»- биллиард на эллиптическом столе с лузами в фокусах.На этом столе, посылая шары из одного фокуса в любом направлении можно всё время выигрывать.
Фокальное свойство эллипса:
отрезки, соединяющие точку Х с его фокусами, составляют равные углы с касательной, проведенной к эллипсу в точке Х.
В
А
А1
Х
Опыт 2. Источник света расположен в точке F1.Лучи света , отразившись от края зеркальной изогнутой полоски формы эллипса, осветят(зажгут) бумагу в точке F2.
Вопрос
Почему освещается(загорается) бумага? Объяснить.
Демонстрация опытов учащимися
Слайд 11Эллипс в жизни
1 . Очертание верхнего
слоя воды в стакане
2.Ломтики колбасы
3.Сечение прямого
цилиндра плоскостью4.Сечение конуса плоскостью
Замечательное оптическое свойство эллипса лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека , стоящего в другом фокусе, слышна так хорошо,как будто он находится рядом, хотя расстояние на самом деле велико.
1.
2.
3.
4.
5.
Демонстрация плакатов