Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
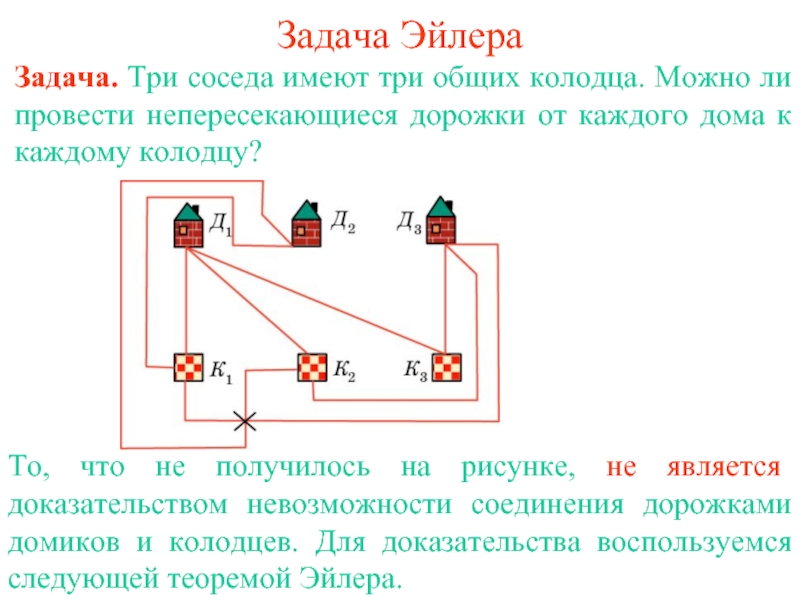
Площади подобных фигур 8 класс
Содержание
- 1. Площади подобных фигур 8 класс
- 2. Пример 1Периметры двух подобных многоугольников относятся как
- 3. Пример 2В круге с центром O проведена
- 4. Упражнение 1Найдите отношение площадей двух квадратов, если
- 5. Упражнение 2Как относятся стороны двух квадратов, если
- 6. Упражнение 3Стороны равносторонних треугольников равны 6 см
- 7. Упражнение 4Как изменится площадь круга, если его
- 8. Упражнение 5Одна из сторон треугольника разделена на
- 9. Упражнение 6Прямая, параллельная стороне треугольника, делит его
- 10. Упражнение 7Площадь данного многоугольника равна 45 см2.
- 11. Упражнение 8Периметры двух подобных многоугольников относятся как
- 12. Упражнение 9Как изменится площадь многоугольника, если каждая
- 13. Упражнение 10Периметры двух правильных n - угольников
- 14. Упражнение 11Найдите отношение площадей правильных шестиугольников, вписанного и описанного около данной окружности.Ответ: 3:4.
- 15. Упражнение 12Две окружности, радиусов R и r
- 16. Упражнение 13Фигура Ф' получена из фигуры Ф
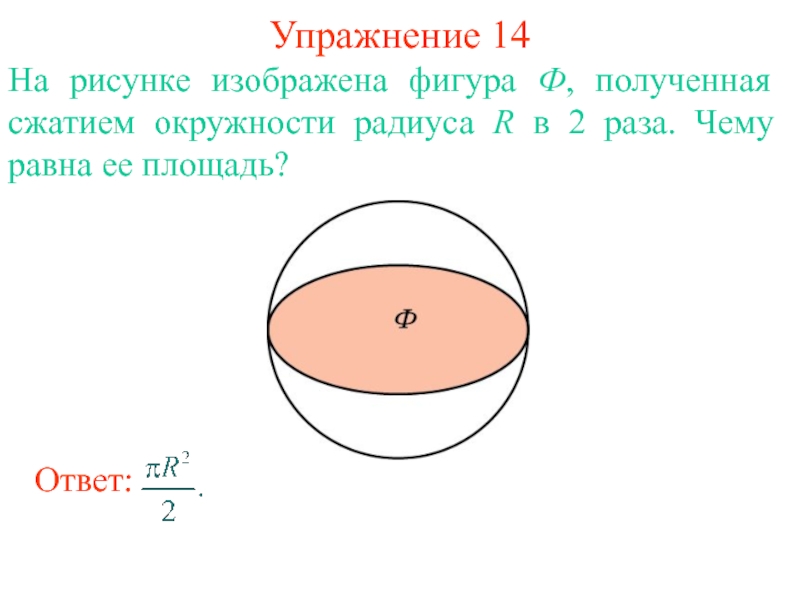
- 17. Упражнение 14На рисунке изображена фигура Ф, полученная
- 18. Скачать презентанцию
Пример 1Периметры двух подобных многоугольников относятся как 1 : 2. Как относятся их площади?Ответ: 1 : 4.
Слайды и текст этой презентации
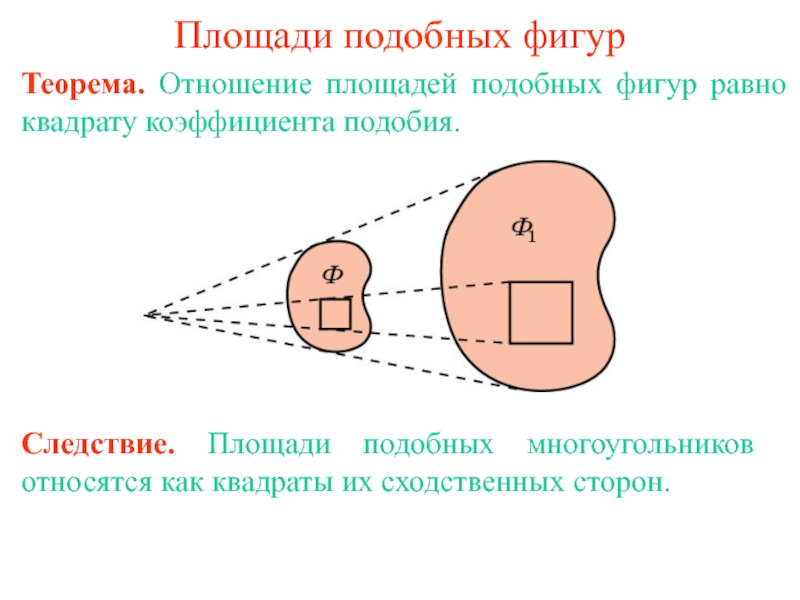
Слайд 1Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента
подобия.
Слайд 2Пример 1
Периметры двух подобных многоугольников относятся как 1 : 2.
Как относятся их площади?
Ответ: 1 : 4.
Слайд 3Пример 2
В круге с центром O проведена хорда AB. На
радиусе OA, как на диаметре, описана окружность. Докажите, что площади
двух сегментов, отсекаемых хордой AB от обоих кругов, относятся как 4 : 1.Решение: Заметим, что большая окружность получается из малой гомотетией с центром в точке A и коэффициентом 2. При этой гомотетии сегмент малой окружности переходит в сегмент большой окружности. Следовательно, отношение их площадей равно 4 : 1.
Слайд 4Упражнение 1
Найдите отношение площадей двух квадратов, если отношение сторон этих
квадратов равно: а) 2:3; б)
; в) 1 : 1,5.Ответ: а) 4 : 9;
б) 2 : 3;
в) 1 : 2,25.
Слайд 5Упражнение 2
Как относятся стороны двух квадратов, если отношение площадей этих
квадратов равно: а) 4 : 9; б) 3 : 4;
в) 0,5 : 2?Ответ: а) 2 : 3;
в) 1 : 2.
Слайд 6Упражнение 3
Стороны равносторонних треугольников равны 6 см и 7 см.
Чему равно отношение их площадей?
Ответ: 36 : 49.
Слайд 7Упражнение 4
Как изменится площадь круга, если его диаметр: а) увеличить
в 2 раза; б) уменьшить в 5 раз?
Ответ: а) Увеличится
в 4 раза; б) уменьшится в 25 раз.
Слайд 8Упражнение 5
Одна из сторон треугольника разделена на три равные части
и через точки деления проведены прямые, параллельные другой стороне. Найдите
отношения площади данного треугольника к площадям треугольников, отсеченных построенными прямыми.Ответ: 9 : 4 : 1.
Слайд 9Упражнение 6
Прямая, параллельная стороне треугольника, делит его на две равновеликие
части. В каком отношении эта прямая делит другие стороны треугольника?
Слайд 10Упражнение 7
Площадь данного многоугольника равна 45 см2. Чему равна площадь
многоугольника, ему подобного, если сходственные стороны многоугольников равны 15 см
и 10 см?Ответ: 20 см2.
Слайд 11Упражнение 8
Периметры двух подобных многоугольников относятся как 3:5. Площадь большего
многоугольника равна 40 м2. Найдите площадь второго многоугольника.
Ответ: 14,4 м2.
Слайд 12Упражнение 9
Как изменится площадь многоугольника, если каждая из его сторон:
а) увеличится в n раз; б) уменьшится в m раз
(а величины углов не изменятся)?Ответ: а) Увеличится в n2 раз;
б) уменьшится в m2 раз.
Слайд 13Упражнение 10
Периметры двух правильных n - угольников относятся как a:b.
Как относятся их площади?
Ответ: a2 : b2.
Слайд 14Упражнение 11
Найдите отношение площадей правильных шестиугольников, вписанного и описанного около
данной окружности.
Ответ: 3:4.
Слайд 15Упражнение 12
Две окружности, радиусов R и r касаются внутренним образом.
Через точку касания проведена хорда, которая отсекает от внешней окружности
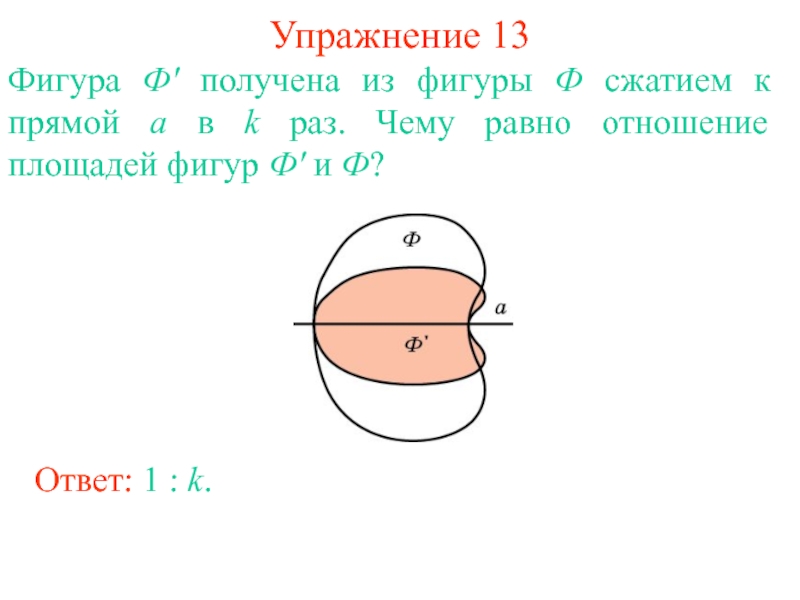
сегмент площади S. Найдите площадь сегмента, отсекаемого этой хордой от внутренней окружности.
Слайд 16Упражнение 13
Фигура Ф' получена из фигуры Ф сжатием к прямой
a в k раз. Чему равно отношение площадей фигур Ф'
и Ф?Ответ: 1 : k.
Слайд 17Упражнение 14
На рисунке изображена фигура Ф, полученная сжатием окружности радиуса
R в 2 раза. Чему равна ее площадь?
