Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие движения
Содержание
- 1. Понятие движения
- 2. План урокаОсевая симметрияЦентральная симметрияПрактическая работаПонятие отображения плоскости на себяПонятие движенияРешение задачИтоги урока
- 3. Осевая симметрияКакие точки называются симметричными относительно
- 4. Центральная симметрияКакие точки называются симметричными относительно
- 5. Практическая работа 1Постройте точки симметричные даннымАВА1В1LFEOE1F1
- 6. Отображение плоскости на себяПусть каждой точке
- 7. Понятие движенияКакими общими свойствами обладают осевая и
- 8. Решение задачРешить задачу № 1153 (учебник)
- 9. Итог урока Осевая и центральная симметрия -
- 10. До скорой встречи!Урок окончен
- 11. Скачать презентанцию
План урокаОсевая симметрияЦентральная симметрияПрактическая работаПонятие отображения плоскости на себяПонятие движенияРешение задачИтоги урока
Слайды и текст этой презентации
Слайд 1 ПОНЯТИЕ ДВИЖЕНИЯ
Геометрия 9 класс
Автор: Григорьева Зинаида Валентиновна
Учитель математики
МОУ
Чилинская СОШ Колпашевского района
Слайд 2 План урока
Осевая симметрия
Центральная симметрия
Практическая работа
Понятие отображения плоскости на себя
Понятие
движения
Решение задач
Итоги урока
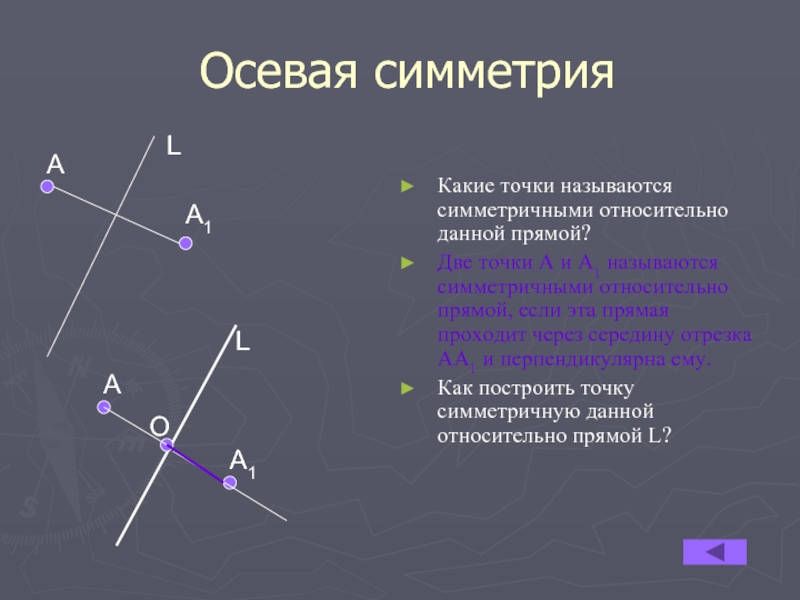
Слайд 3 Осевая симметрия
Какие точки называются симметричными относительно данной прямой?
Две точки
А и А1 называются симметричными относительно прямой, если эта прямая
проходит через середину отрезка АА1 и перпендикулярна ему.Как построить точку симметричную данной относительно прямой L?
А
L
А1
А
О
А1
L
Слайд 4 Центральная симметрия
Какие точки называются симметричными относительно данной точки?
Две точки
А и А1 называются симметричными относительно точки, если эта точка
является серединой отрезка АА1.Как построить точку симметричную данной относительно некоторой точки О?
А
О
А1
А
О
А1
Слайд 6 Отображение плоскости на себя
Пусть каждой точке плоскости ставится в
соответствие какая –то точка этой плоскости, причем любая точка плоскости
оказывается сопоставленной некоторой точке. В таком случае говорят, что дано отображение плоскости на себя.
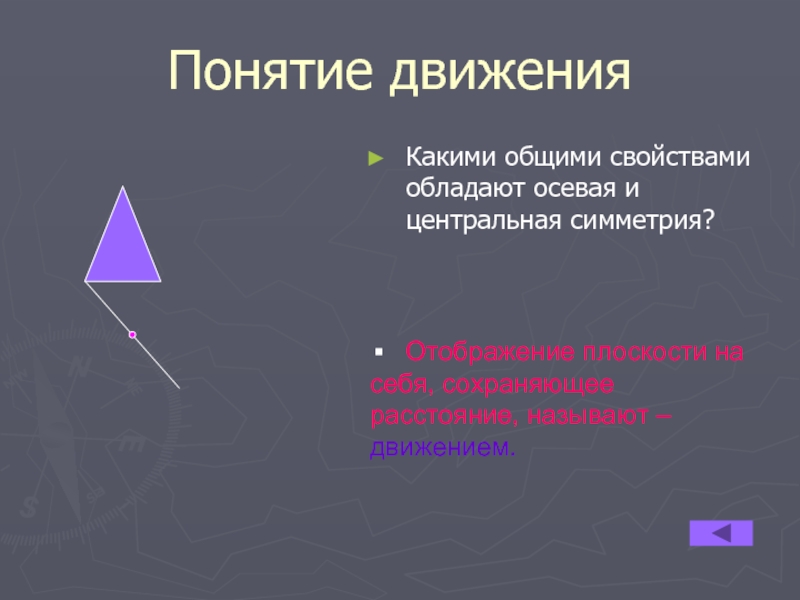
Слайд 7Понятие движения
Какими общими свойствами обладают осевая и центральная симметрия?
Отображение плоскости на себя, сохраняющее расстояние, называют – движением.
Теги