ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ

Содержание

1. ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
2. Дайте определение параллельных прямых.Две прямые на плоскости называются параллельными, если они не пересекаются. ab
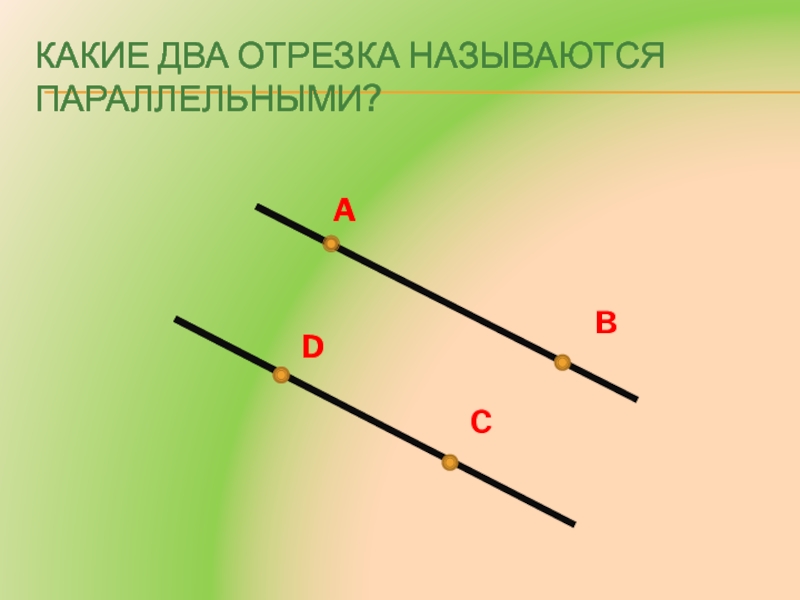
3. Какие два отрезка называются параллельными?ADBC
4. Что такое секущая?Назовите пары углов, которые образуются при пересечении двух прямых секущей?abc12345678
5. Если при пересечении двух прямых секущей накрест
6. Доказательство.
7. 2) Пусть ∟1 и ∟2 не
8. Если при пересечении двух прямых секущей соответственные
9. Если при пересечении двух прямых секущей сумма
10. РЕШИТЕ задачу:1. По данным рисунка докажите, что
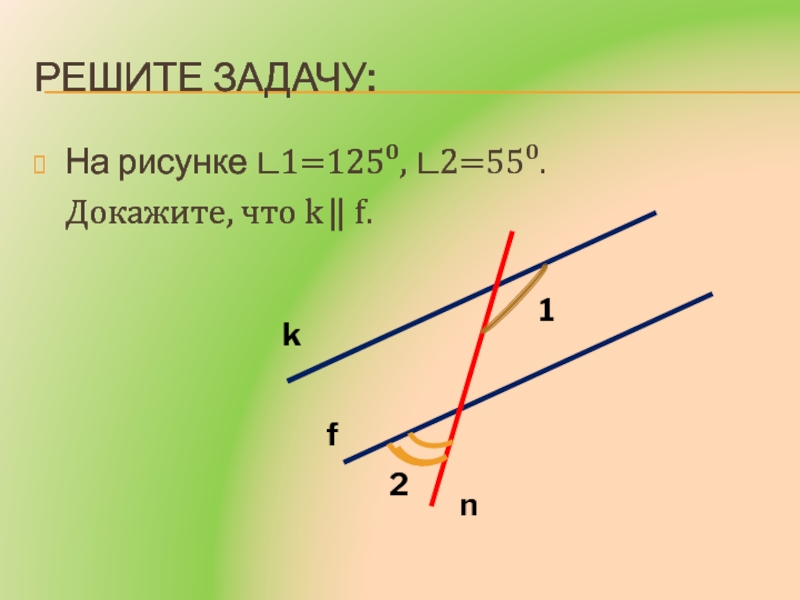
11. Решите задачу:На рисунке ∟1=125⁰, ∟2=55⁰. Докажите, что k ⃦ f.kfn12
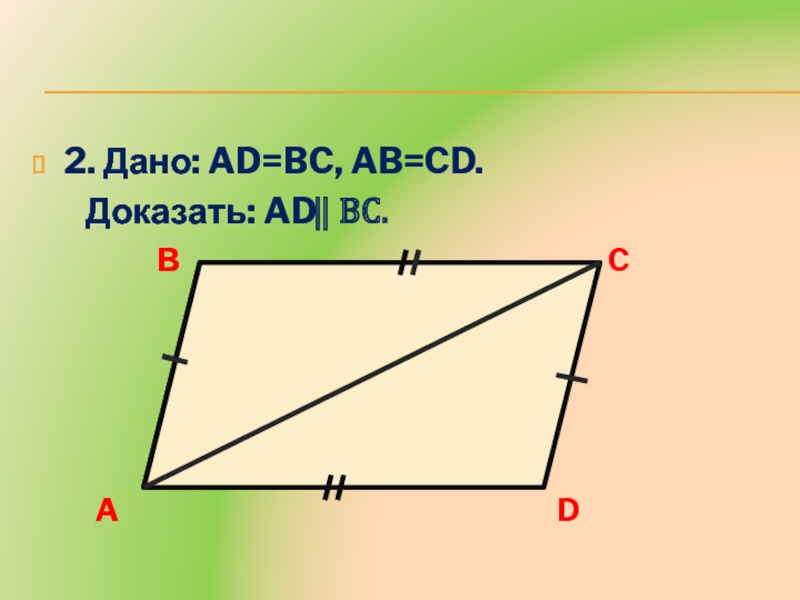
12. 2. Дано: AD=BC, AB=CD. Доказать: AD ⃦ BC.ABCD
13. В классе№ 186(в), № 189.
14. 3.ABCDЧерез точки A и C проведитепрямые a
15. Домашнее задание повторить теорию: п.25-п.26,
16. Скачать презентанцию

Дайте определение параллельных прямых.Две прямые на плоскости называются параллельными, если они не пересекаются. ab

Главная
Геометрия
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ

Слайды и текст этой презентации

Слайд 1ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ

ПРЯМЫХ
Петрова Людмила

Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 126

Слайд 2Дайте определение параллельных прямых.
Две прямые на плоскости называются параллельными, если

они не пересекаются.

a
b

Слайд 3Какие два отрезка называются параллельными?
A
D
B
C

Слайд 4Что такое секущая?
Назовите пары углов, которые образуются при пересечении двух

прямых секущей?
a
b
c
1
2
3
4
5
6
7
8

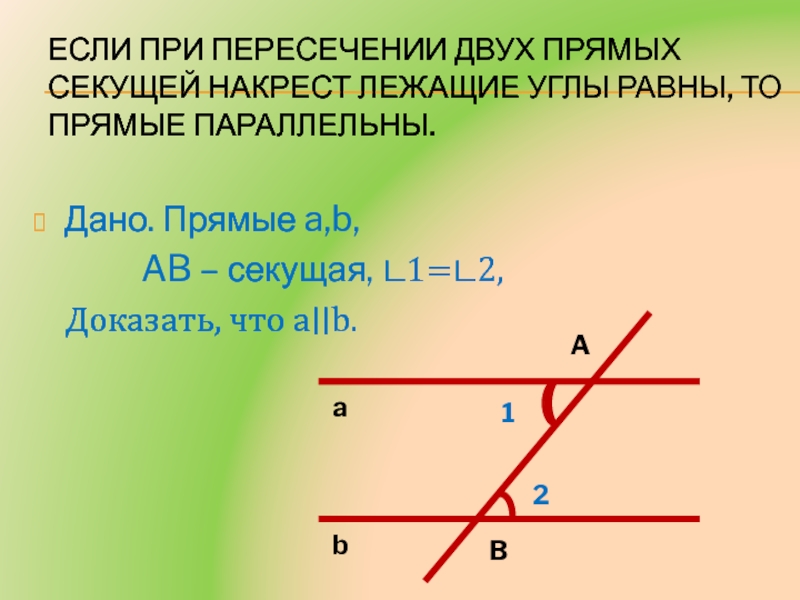
Слайд 5Если при пересечении двух прямых секущей накрест лежащие углы равны,

то прямые параллельны.
Дано. Прямые a,b,

AB – секущая, ∟1=∟2,
Доказать, что a∣∣b.

Слайд 6Доказательство.

1) ∟1 и ∟2 прямые,
a ⊥ AB, b ⊥ AB.
Следовательно,
a ∣∣ b.

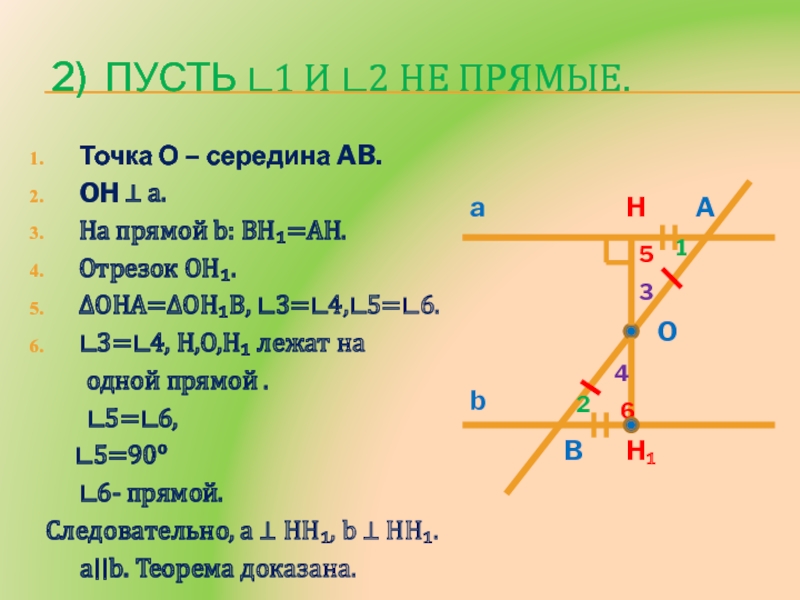
Слайд 7 2) Пусть ∟1 и ∟2 не прямые.
Точка О –

середина AB.
OH ⊥ a.
На прямой b: BH₁=AH.
Отрезок OH₁.
∆OHA=∆OH₁B, ∟3=∟4,∟5=∟6.
∟3=∟4, H,O,H₁

лежат на
одной прямой .
∟5=∟6,
∟5=90о
∟6- прямой.
Следовательно, a ⊥ HH₁, b ⊥ HH₁.
a∣∣b. Теорема доказана.

H₁

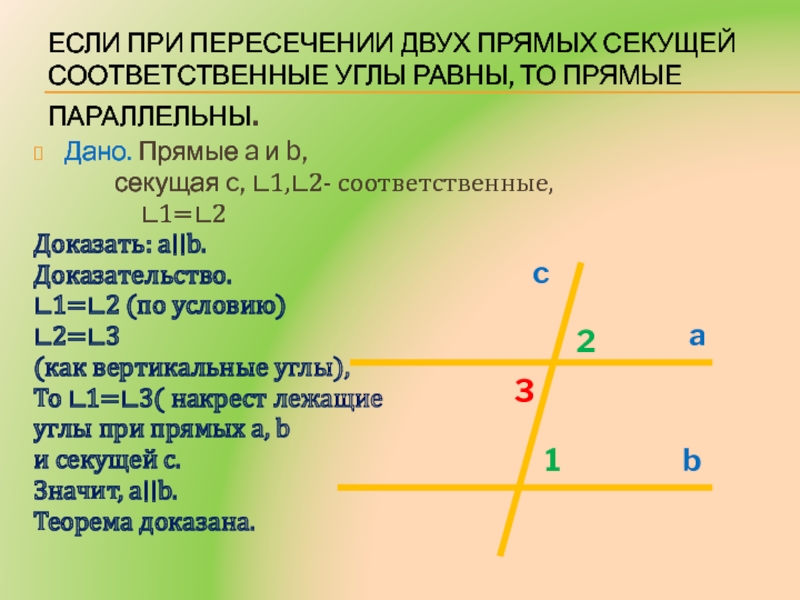
Слайд 8Если при пересечении двух прямых секущей соответственные углы равны, то

прямые параллельны.
Дано. Прямые a и b,

секущая c, ∟1,∟2- соответственные,
∟1=∟2
Доказать: a∣∣b.
Доказательство.
∟1=∟2 (по условию)
∟2=∟3
(как вертикальные углы),
То ∟1=∟3( накрест лежащие
углы при прямых а, b
и секущей с.
Значит, a∣∣b.
Теорема доказана.

Слайд 9Если при пересечении двух прямых секущей сумма односторонних углов равна

180⁰, то прямые параллельны.
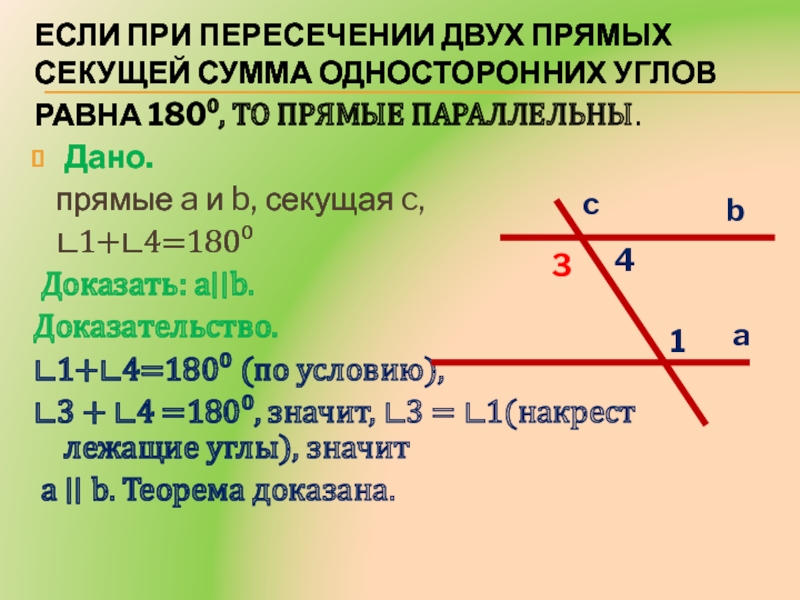
Дано.
прямые a и b,

секущая c,
∟1+∟4=180⁰
Доказать: a∣∣b.
Доказательство.
∟1+∟4=180⁰ (по условию),
∟3 + ∟4 =180⁰, значит, ∟3 = ∟1(накрест лежащие углы), значит
a ∣∣ b. Теорема доказана.