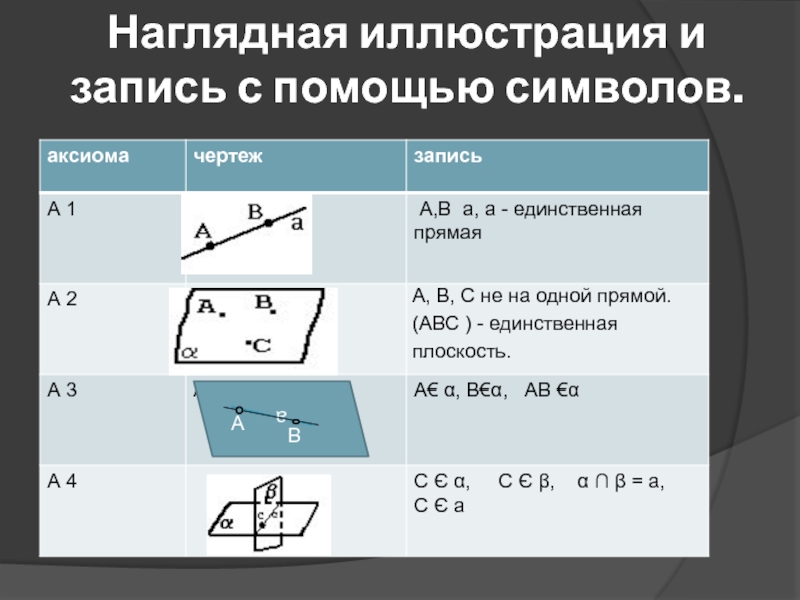
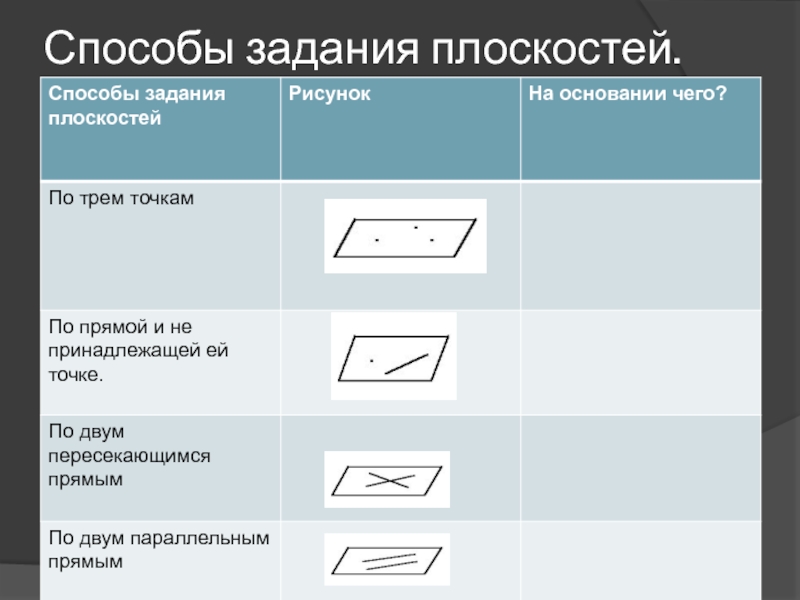
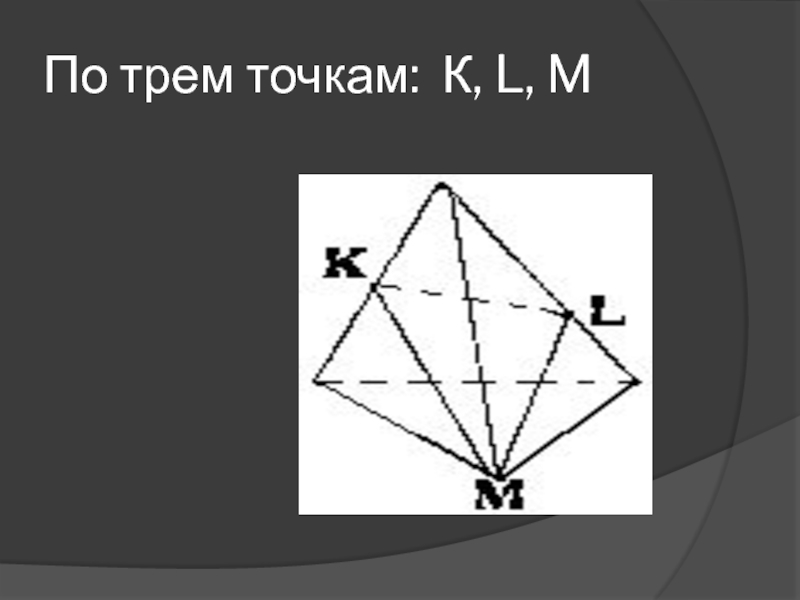
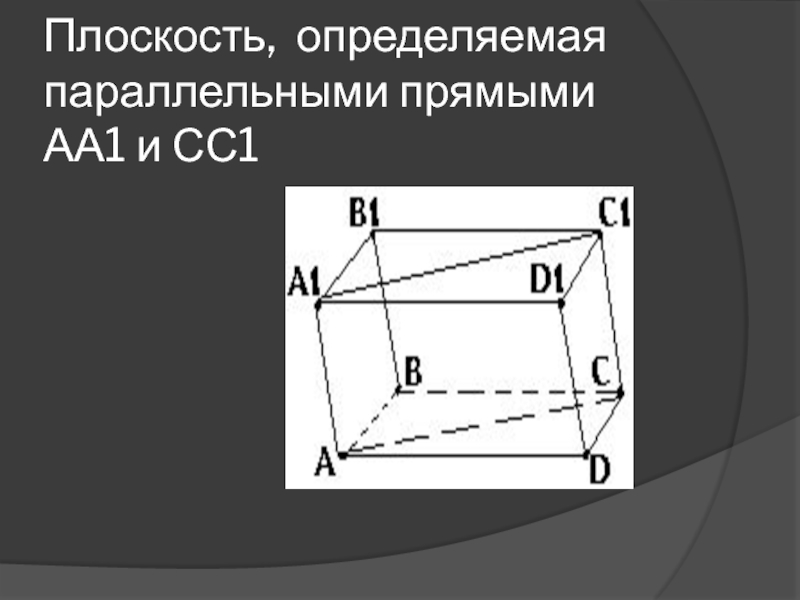
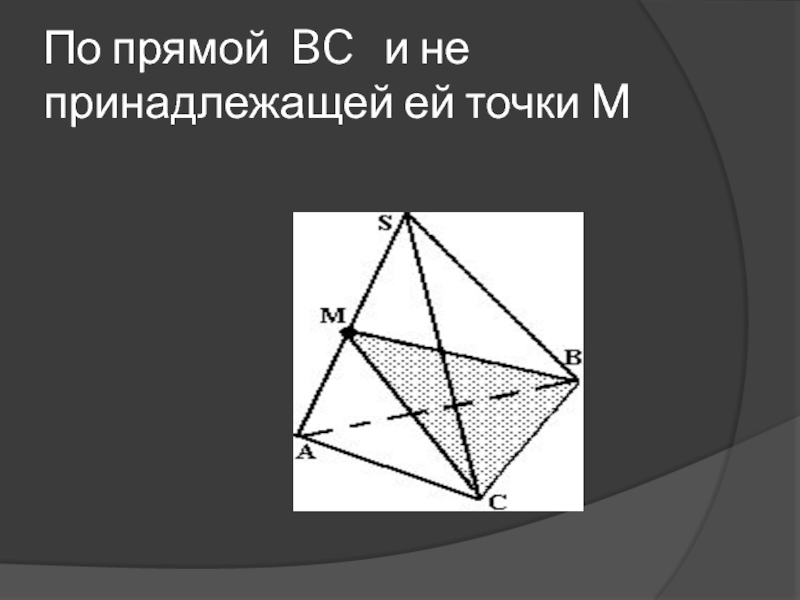
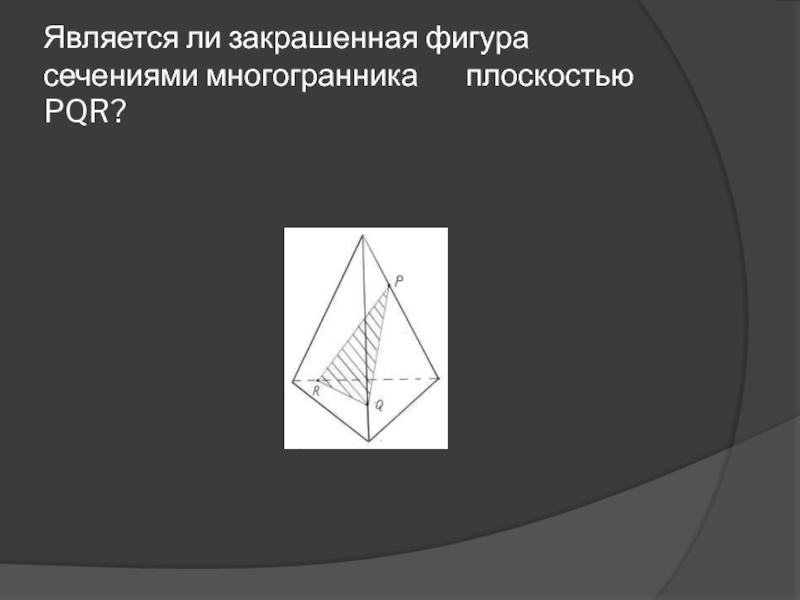
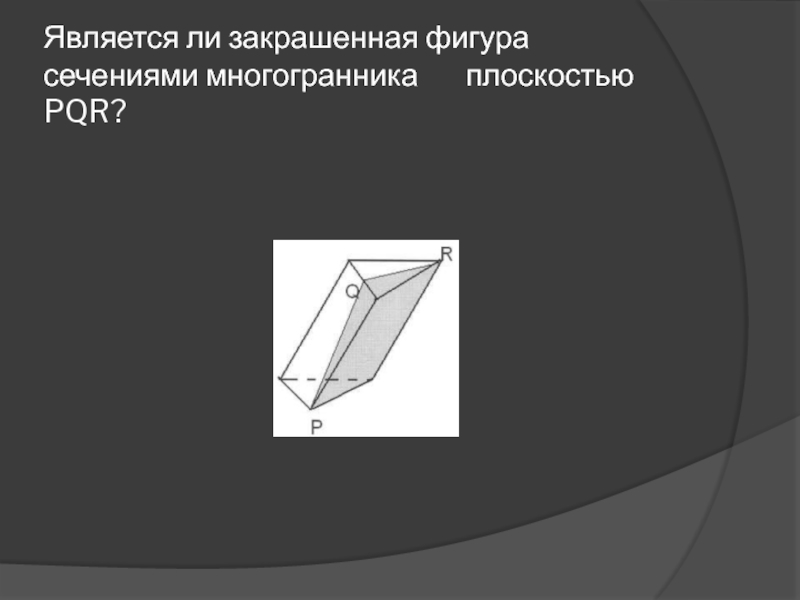
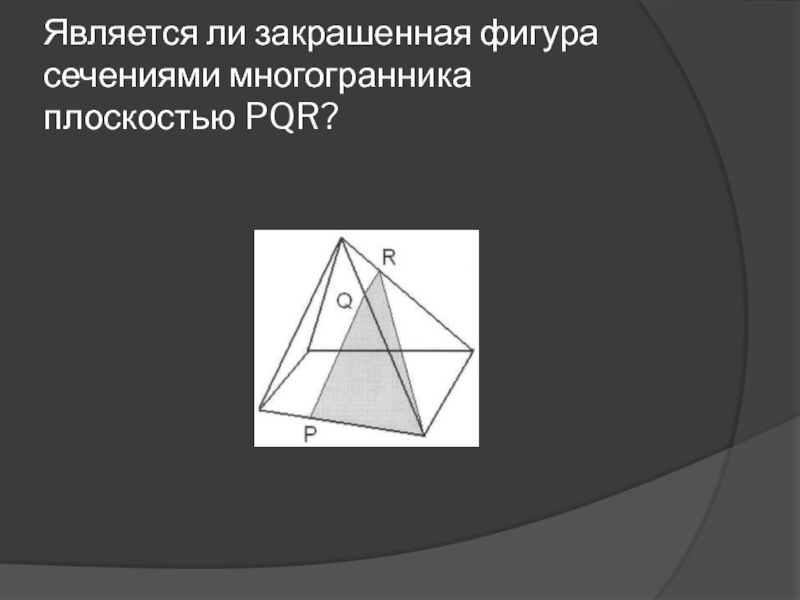
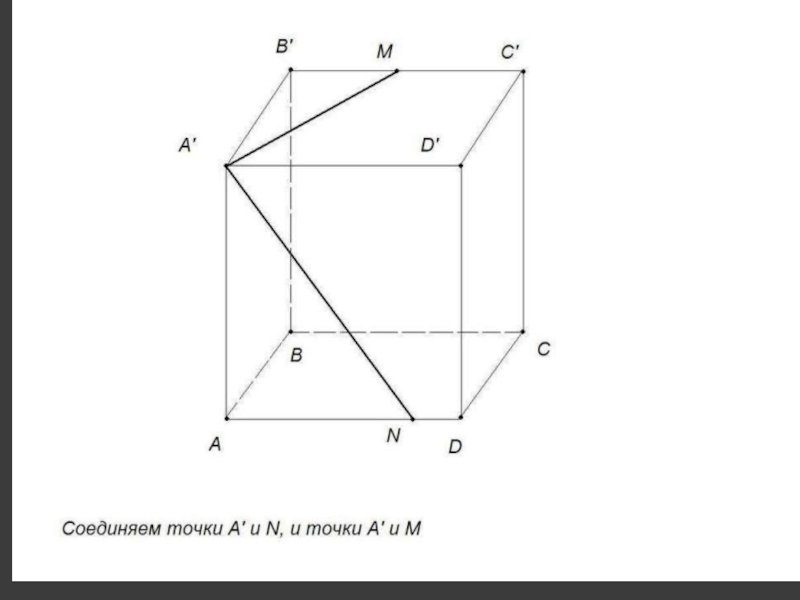
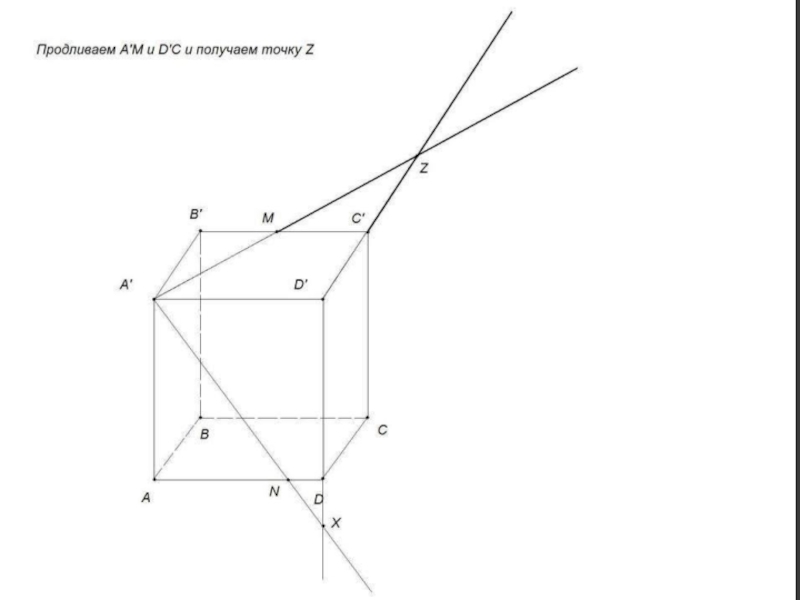
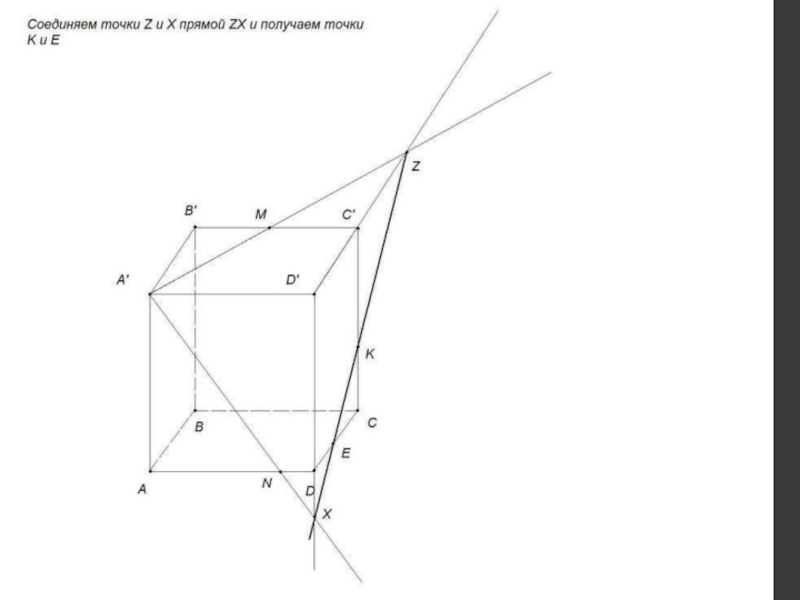
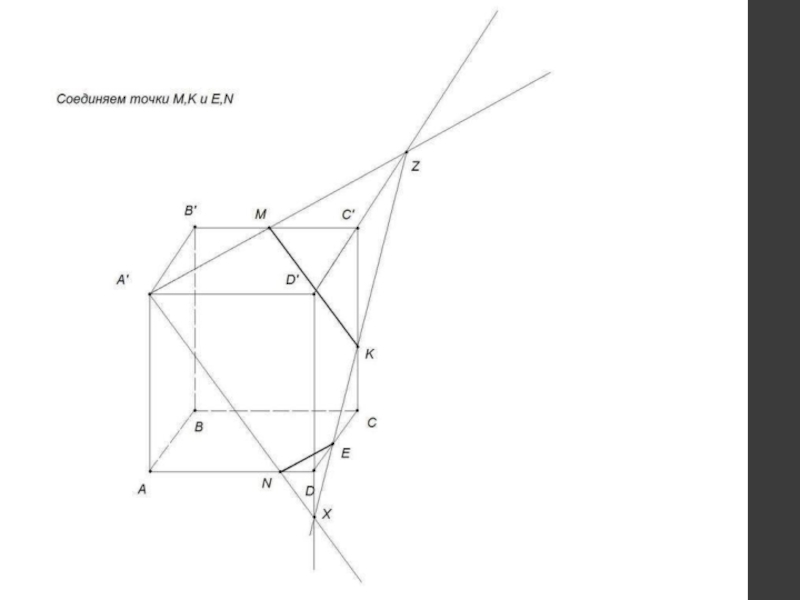
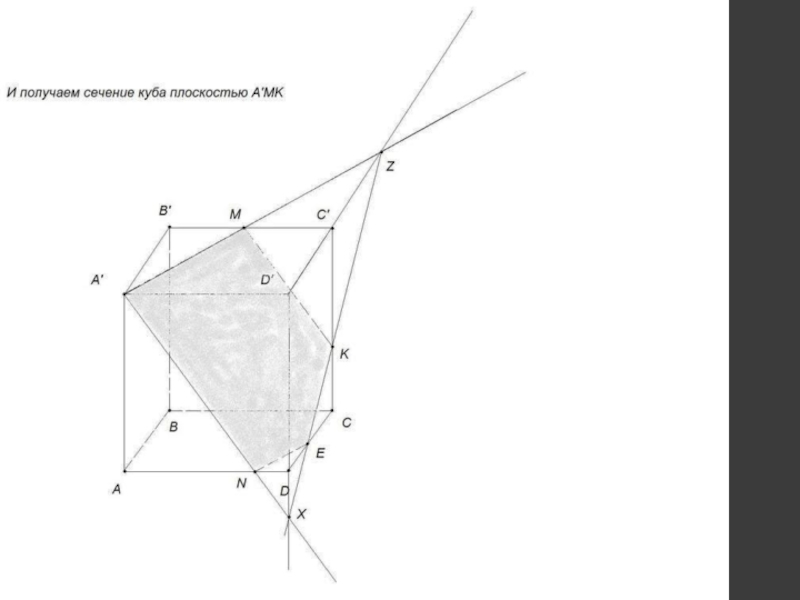
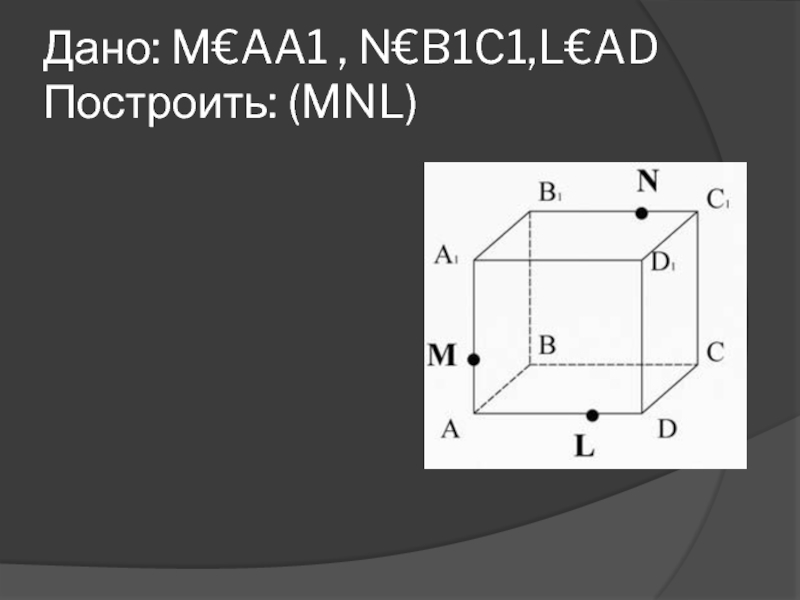
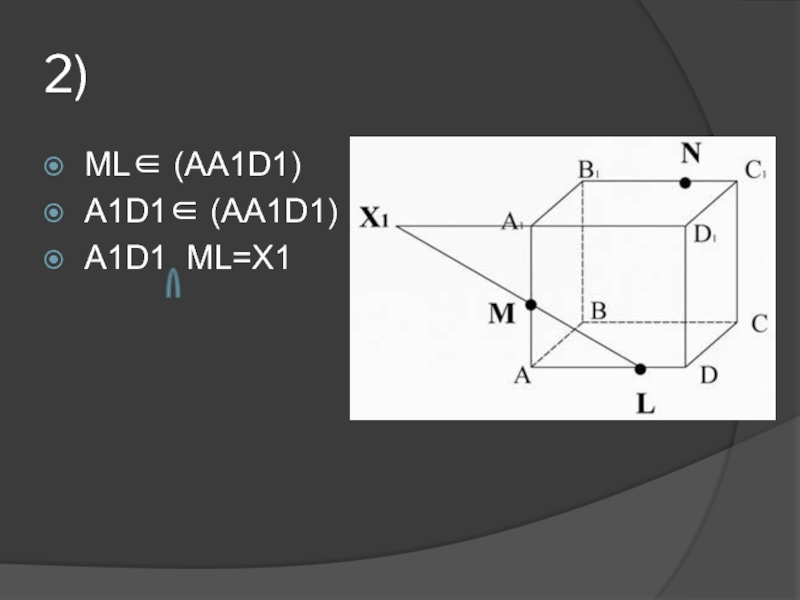
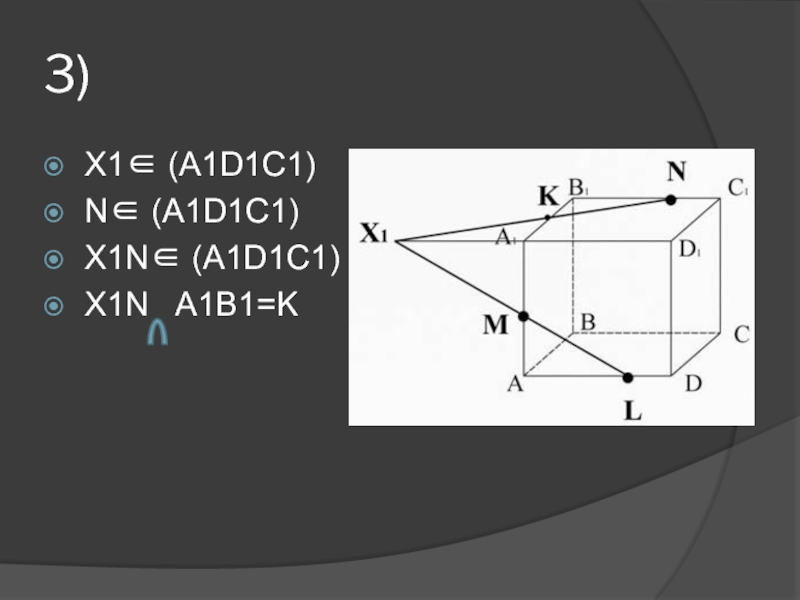
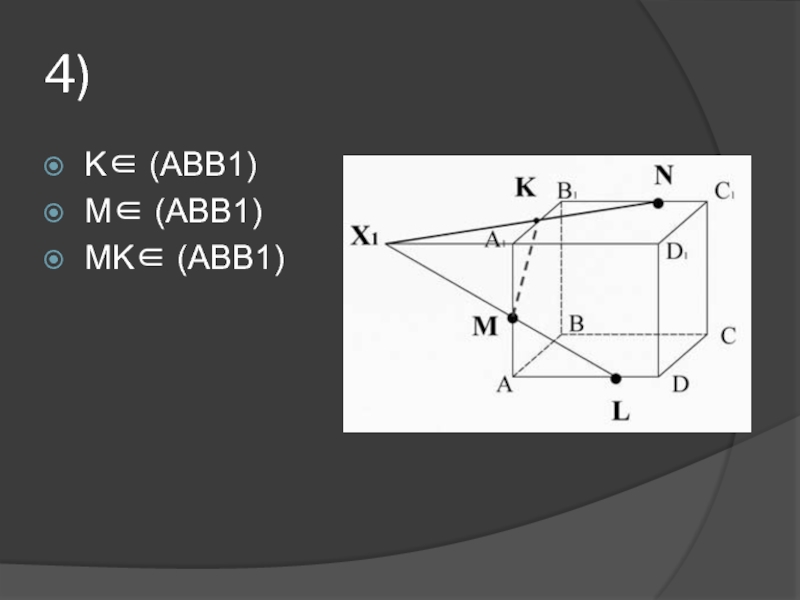
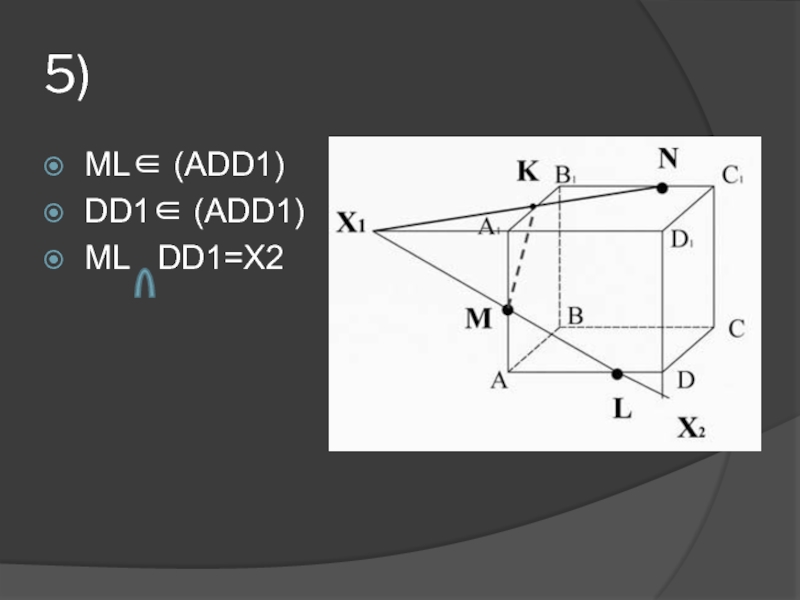
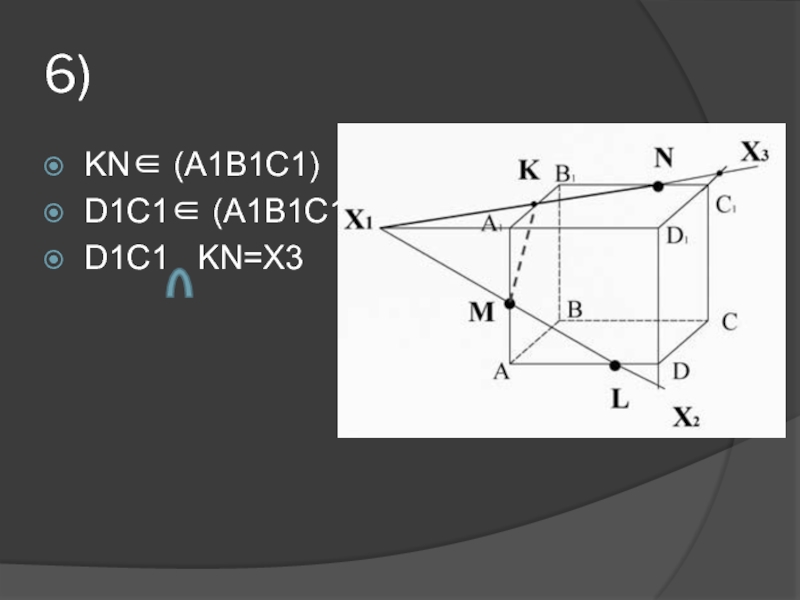
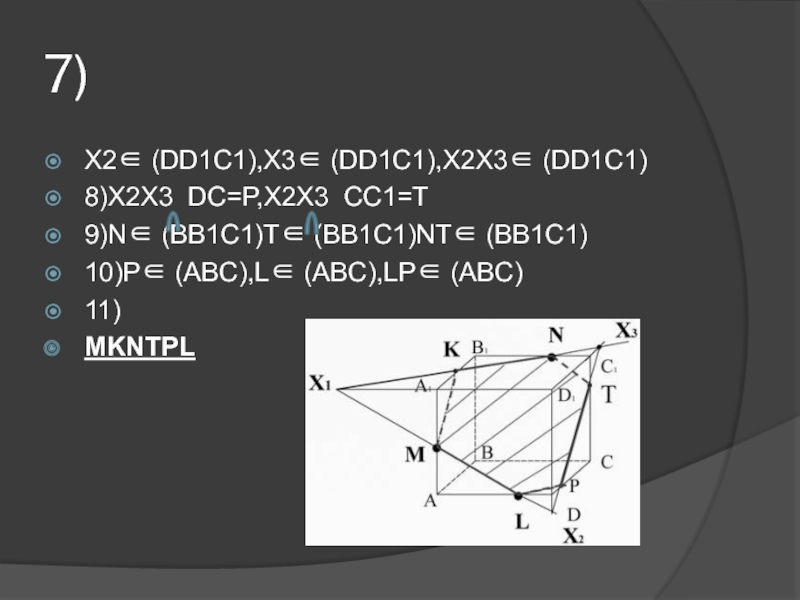
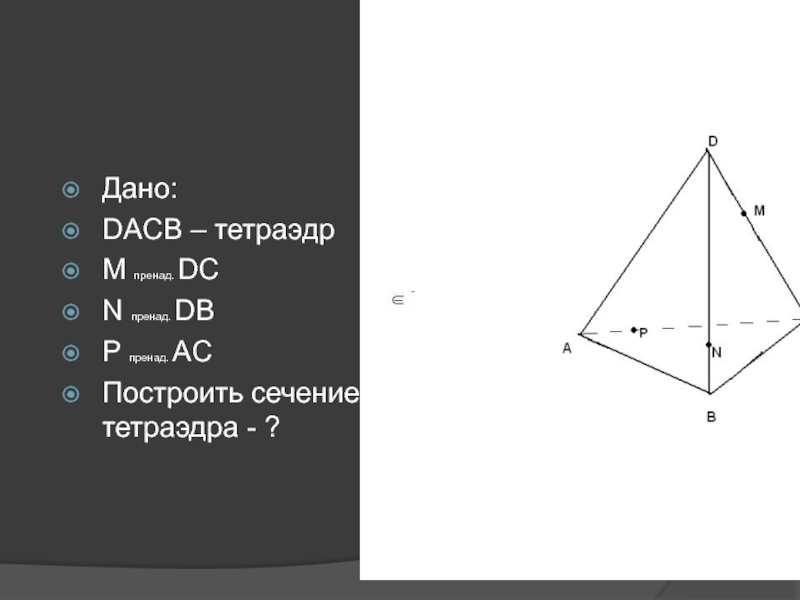
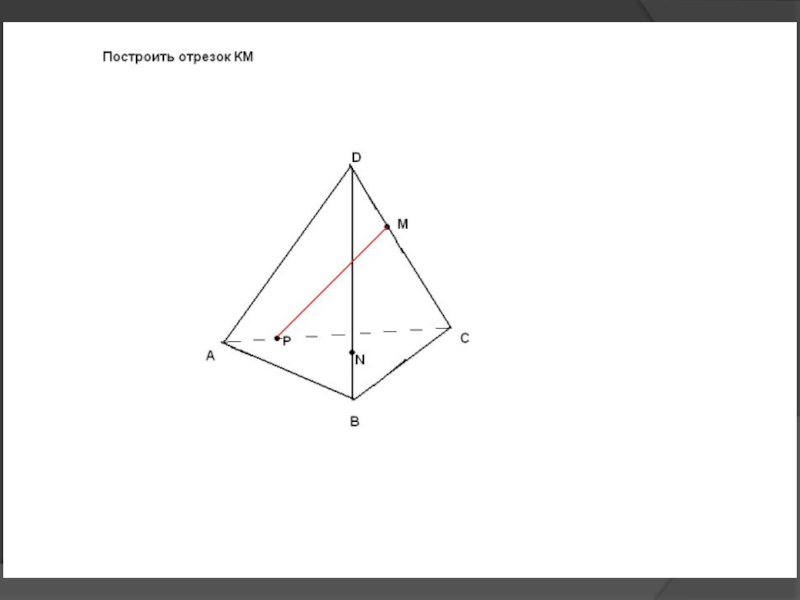
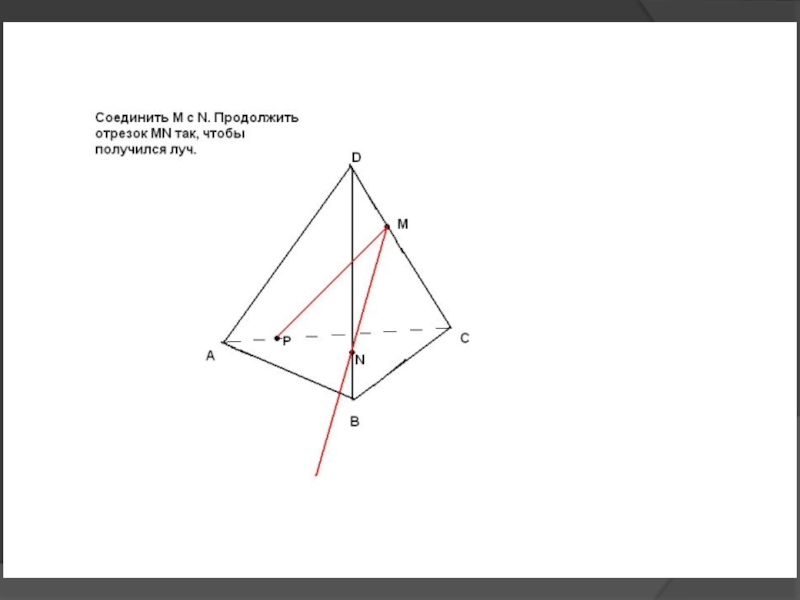
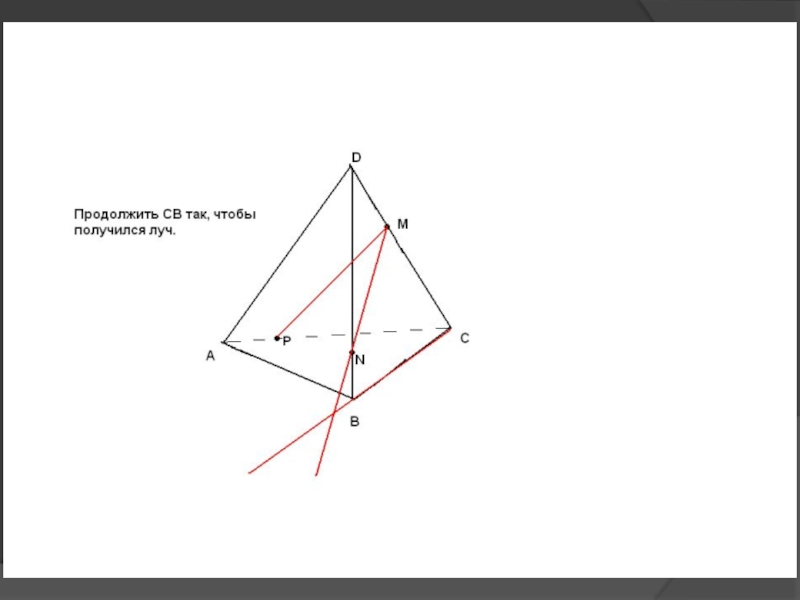
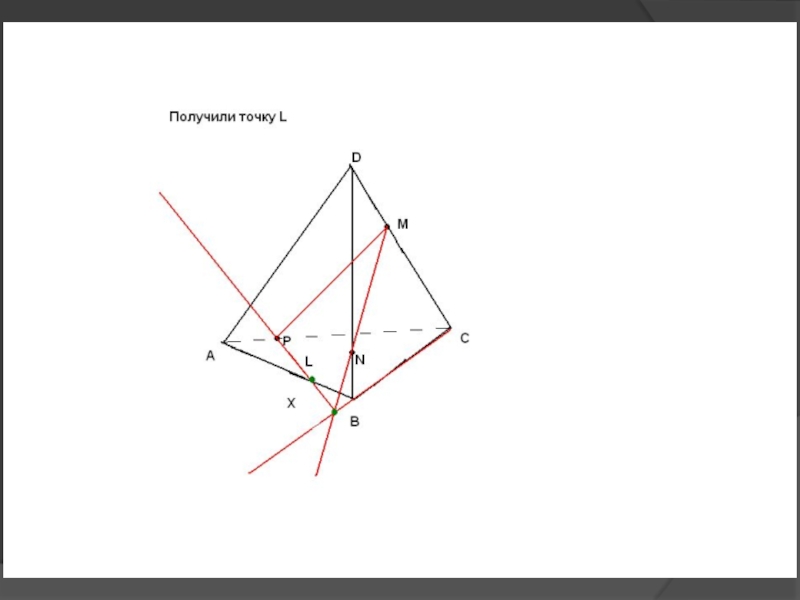
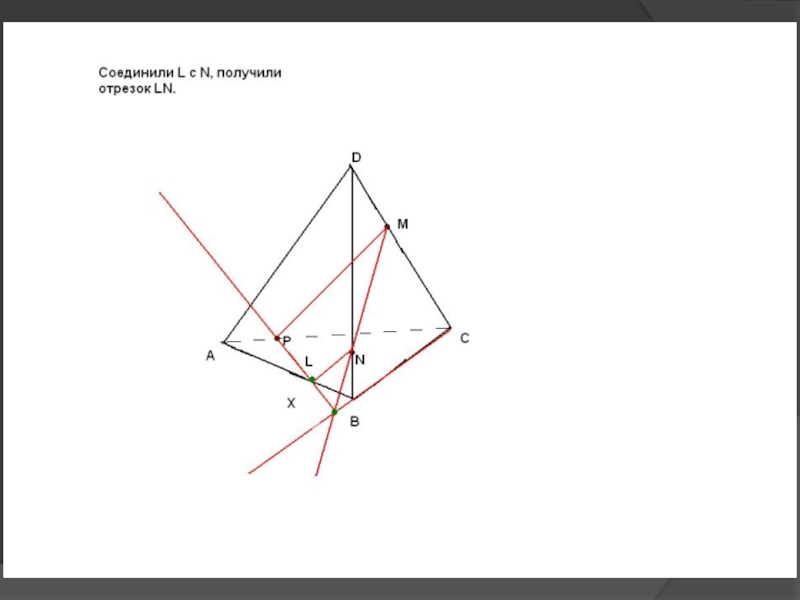
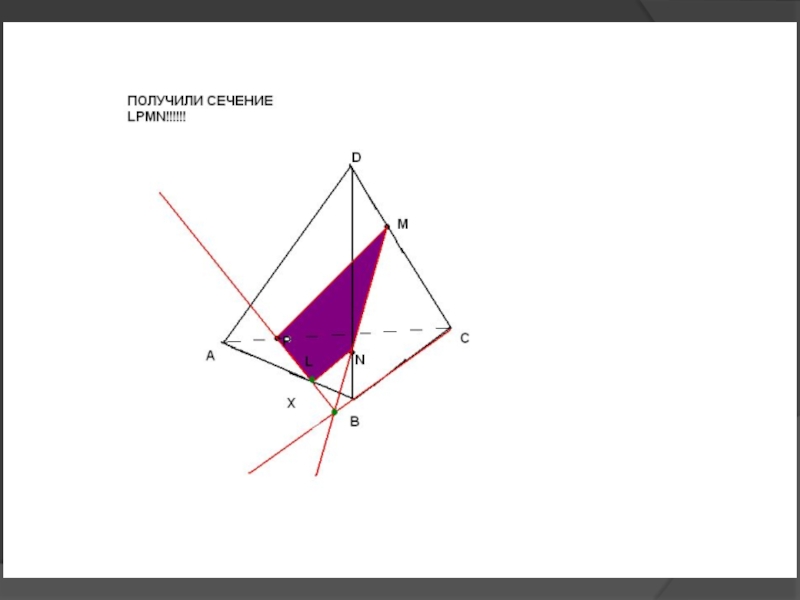
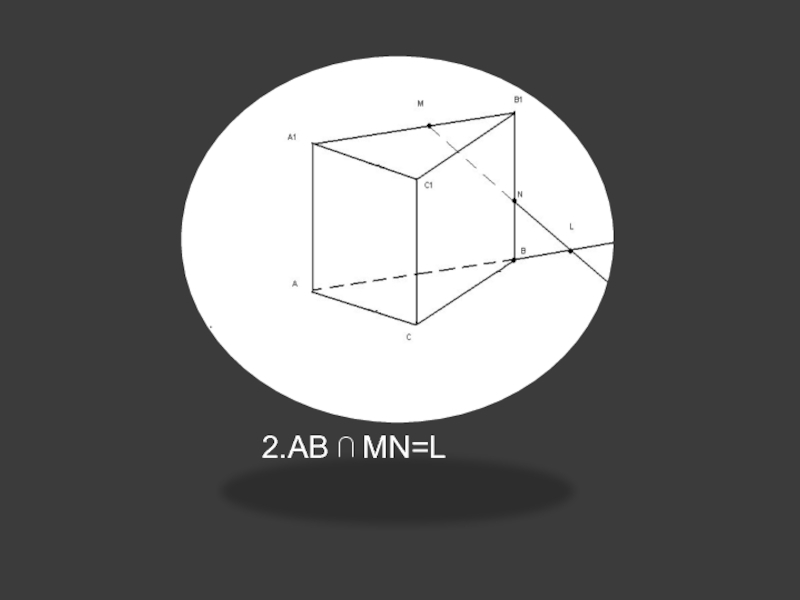
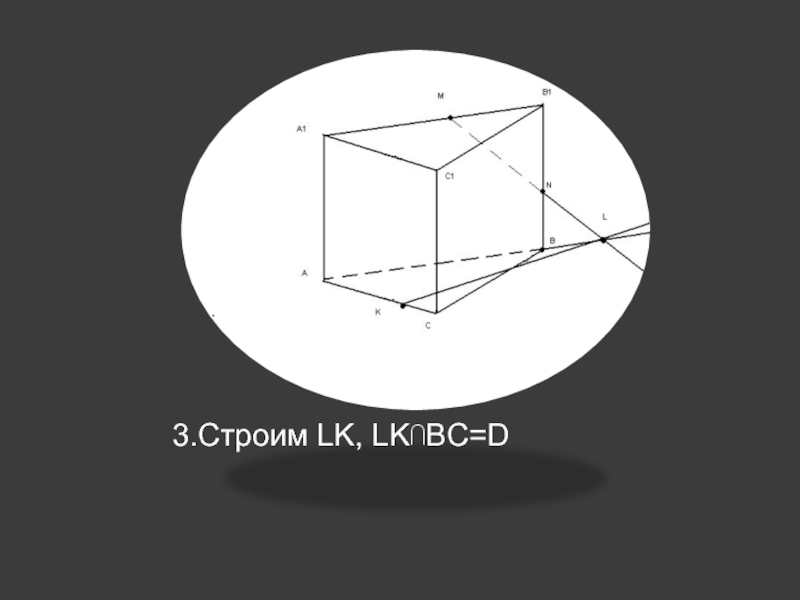
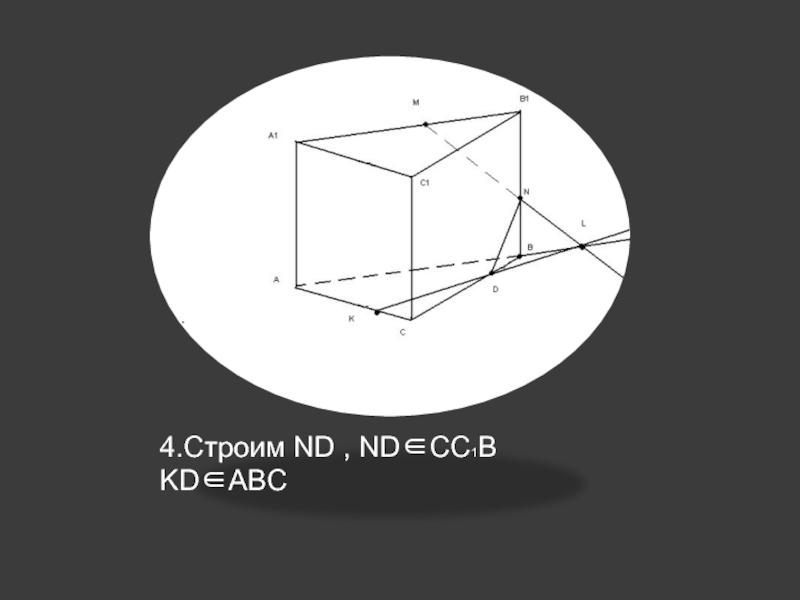
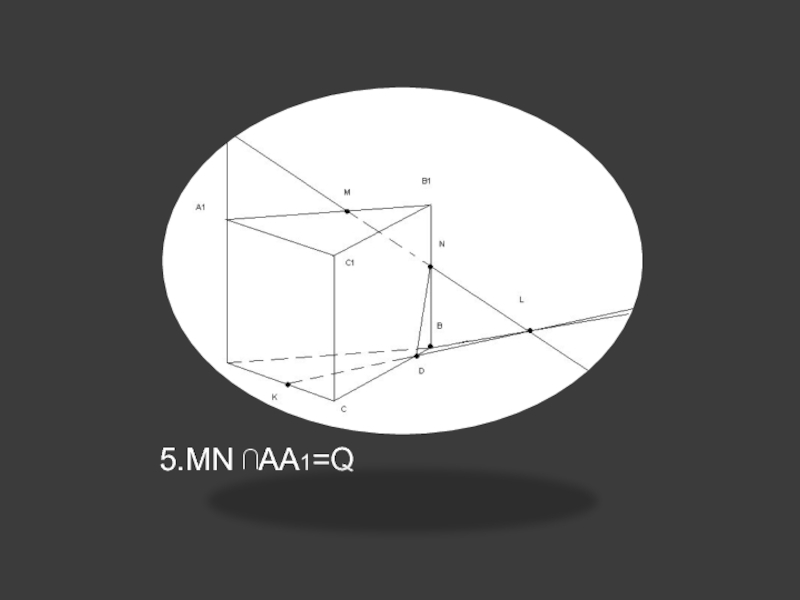
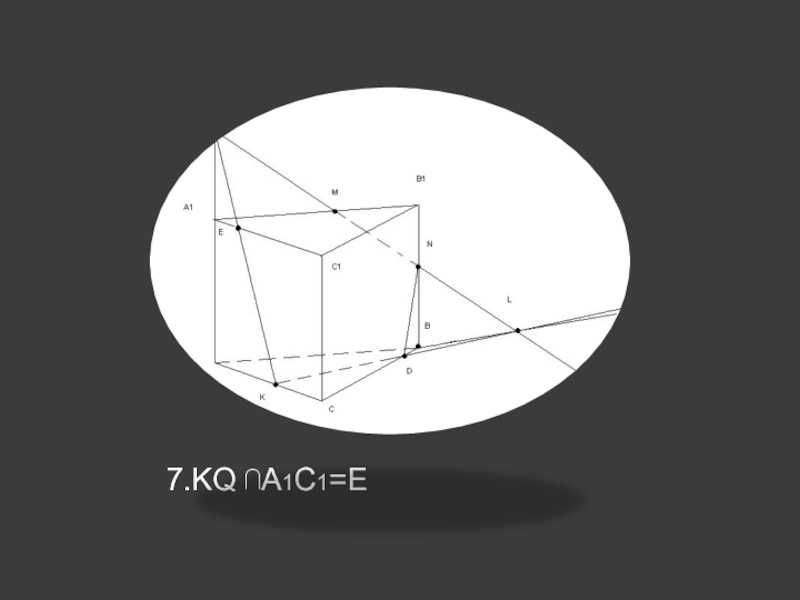
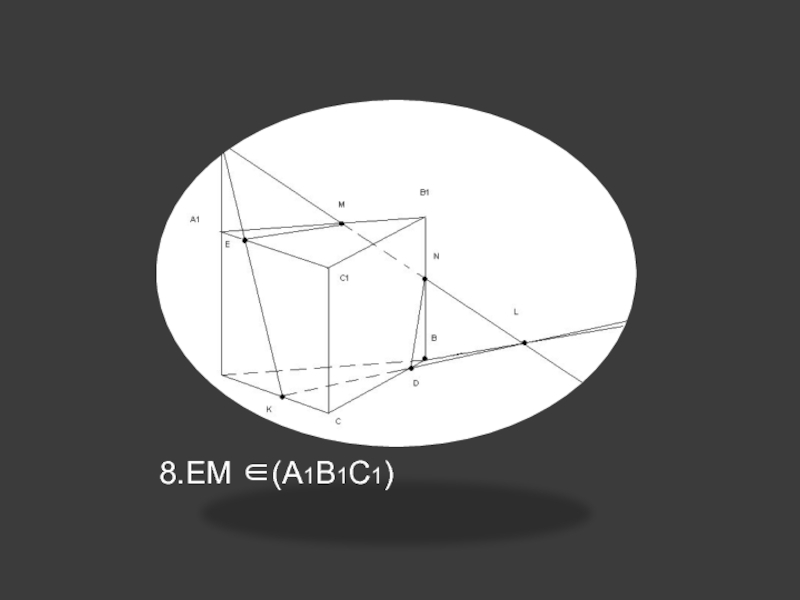
др.
2. Владеть символическим языком геометрии.
3. Воспитывать аккуратность,
коллективизм, ответственность за себя и товарищей, дружбу, любовь к предмету и др. 4. Научить анализировать задачу, работать с учебником, применять свои знания в новой ситуации.