Расстояние между скрещивающимися прямыми

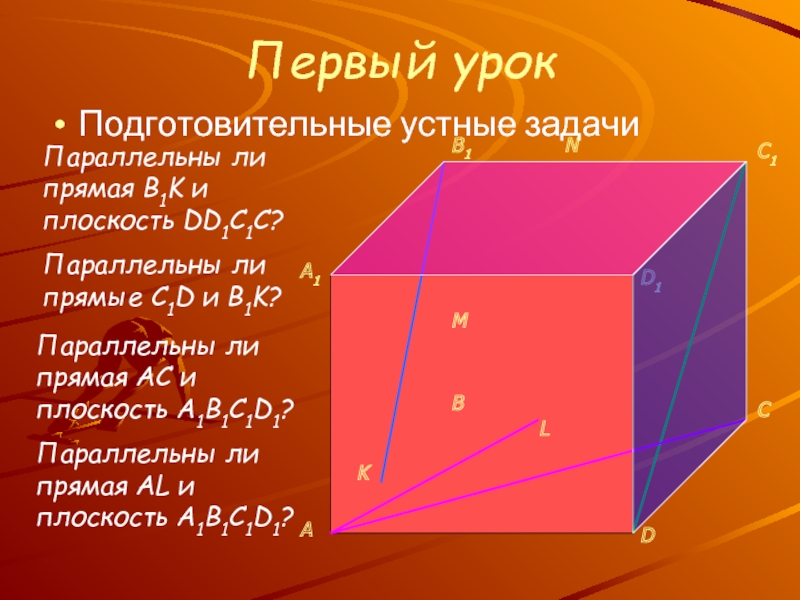
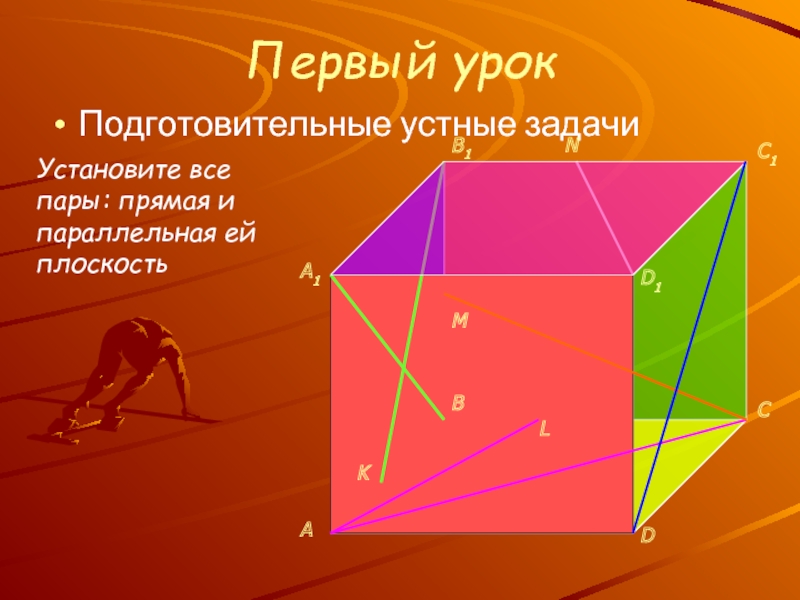
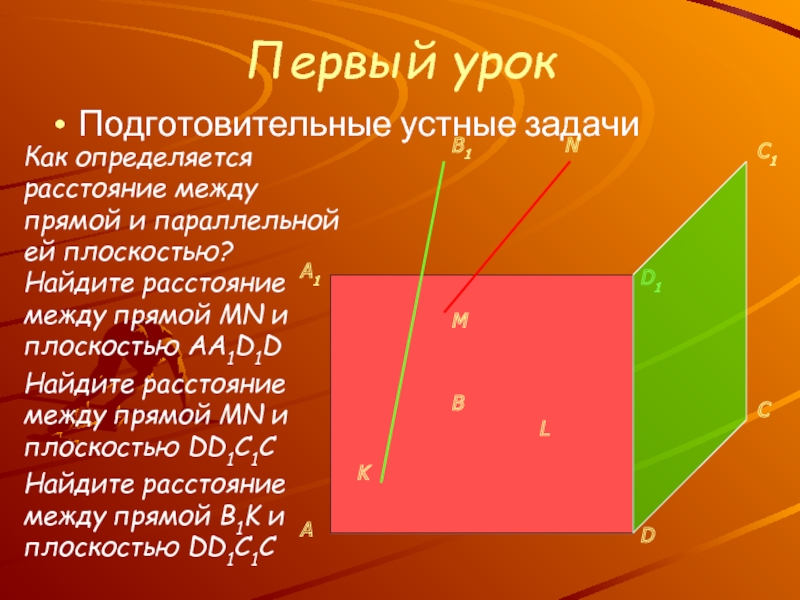
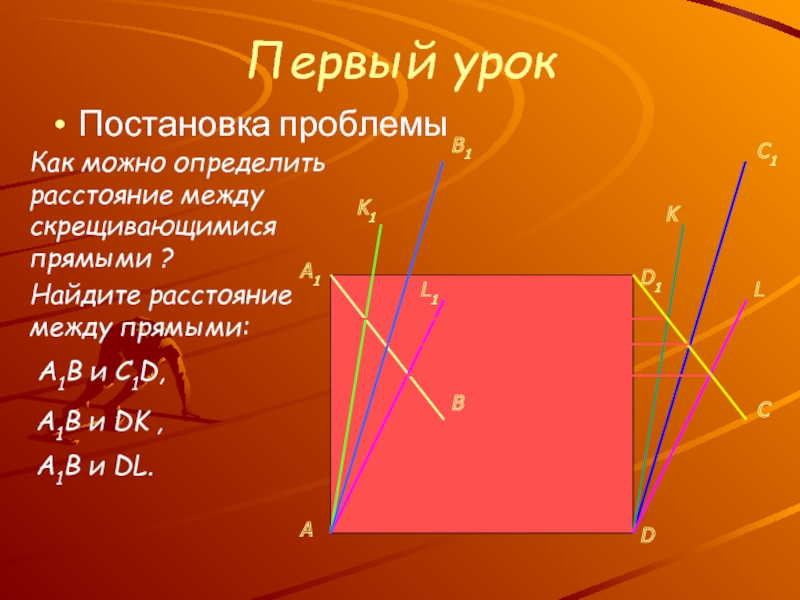
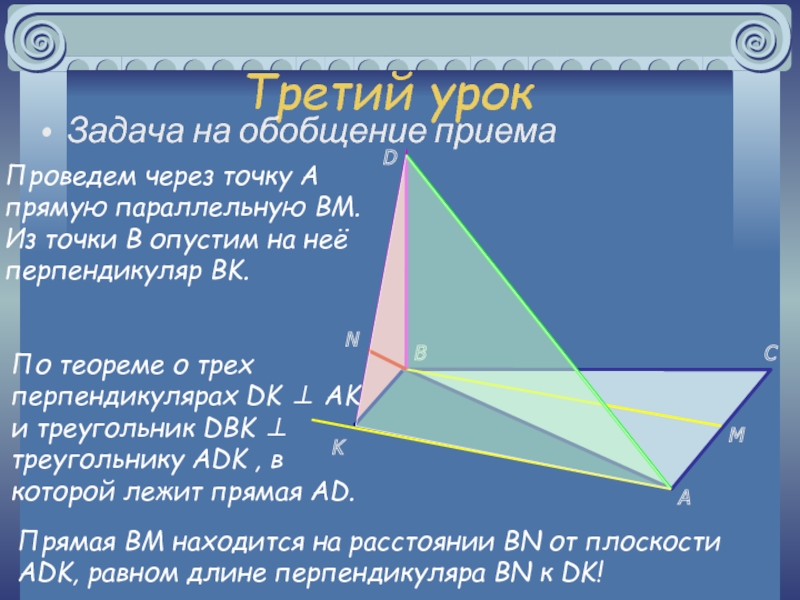
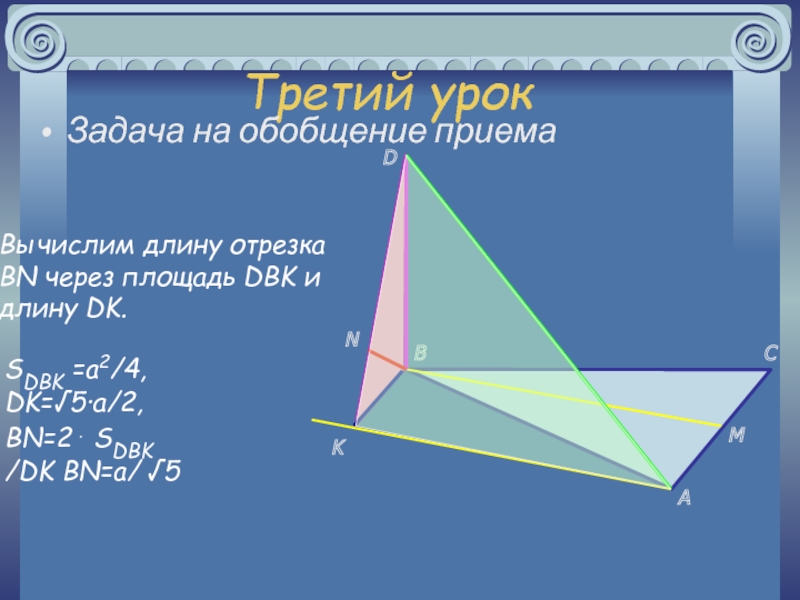
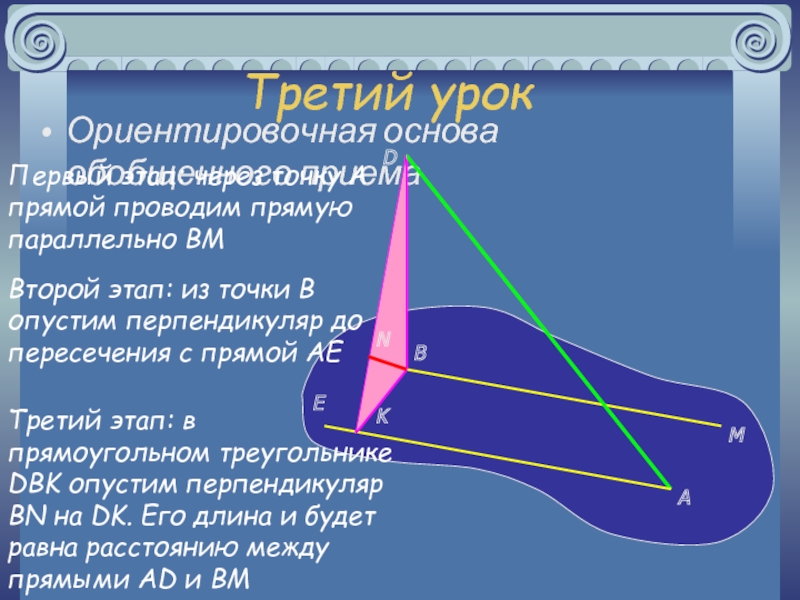
, плоскостями и телами
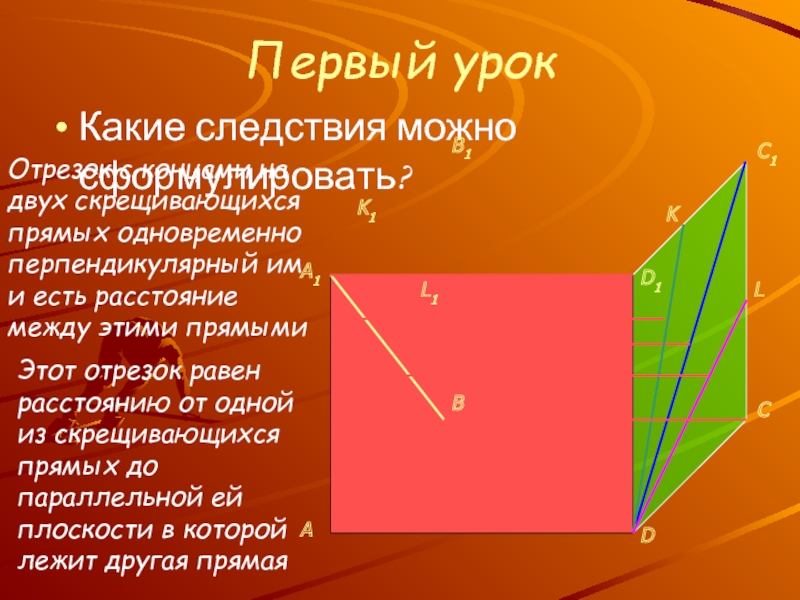
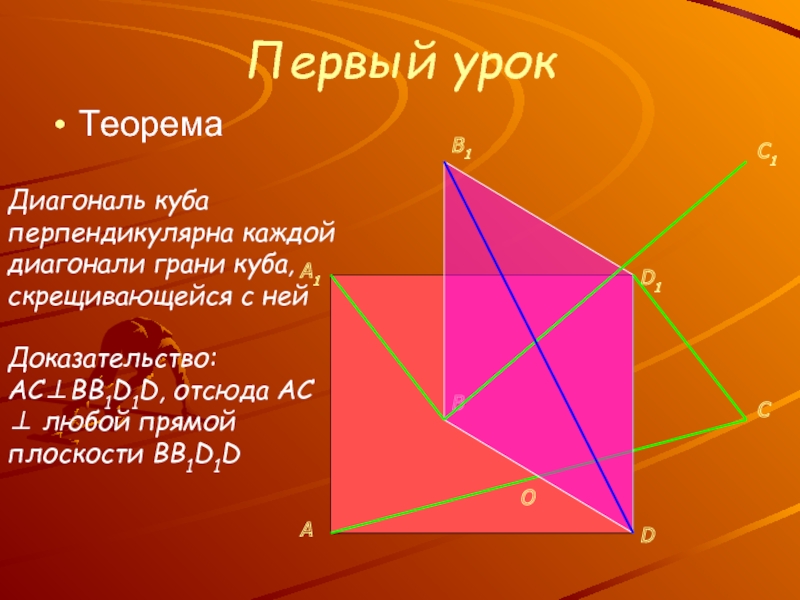
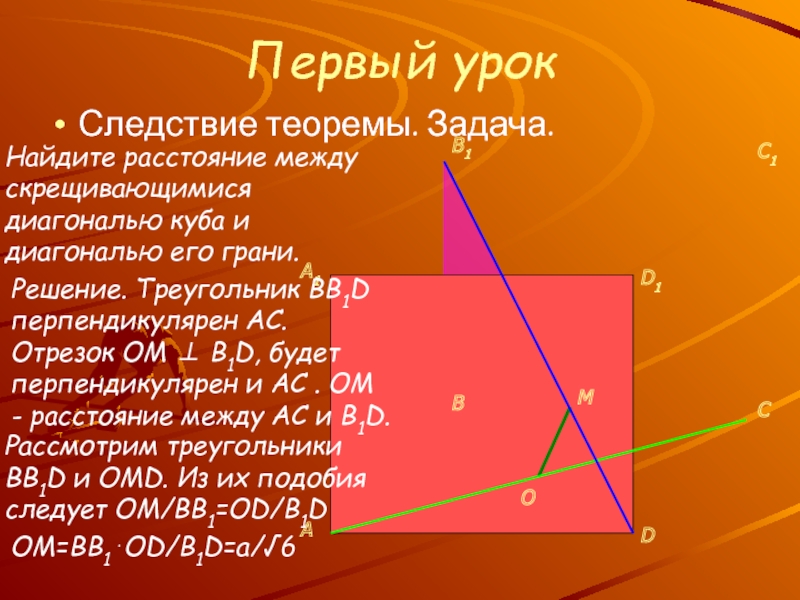
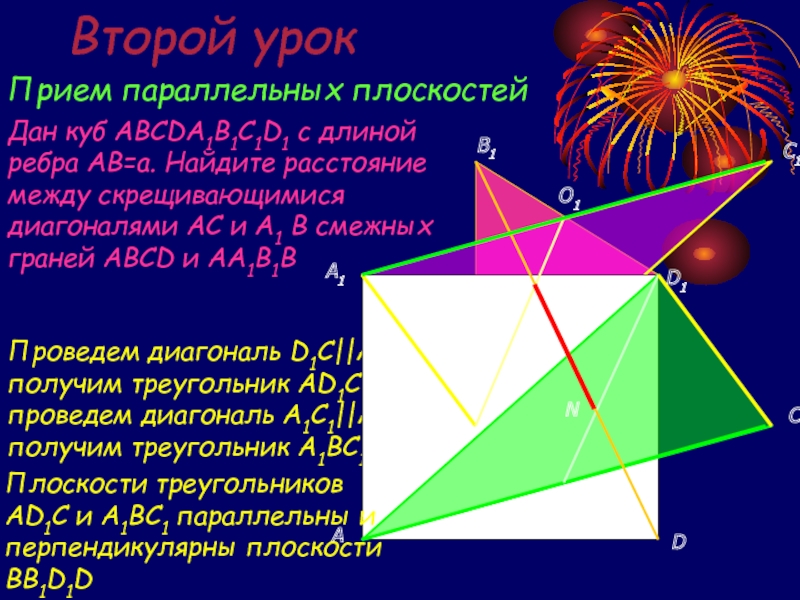
Знакомство с новым понятием: расстояние между скрещивающимися

пространственными объектами: прямыми и плоскостями
Определение нового понятия: расстояние между скрещивающимися

о трех перпендикулярах
Приемы стерео и планиметрических построений
Типовые и проблемные

задачи
Определение и усвоение нового понятия
Второй урок . Решение

ли прямые C1D и B1K?
Параллельны ли прямая AC и плоскость

плоскость

ей плоскостью?

Найдите расстояние между прямой MN и плоскостью AA1D1D
Найдите расстояние

Найдите расстояние между прямой B1K и плоскостью DD1C1C

расстояние между прямыми:
A1B и C1D,
A1B и DK ,
A1B

прямых одновременно перпендикулярный им и есть расстояние между этими прямыми
K1
L1

Этот

ней
Доказательство: AC⊥BB1D1D, отсюда AC ⊥ любой прямой плоскости BB1D1D

подобия следует OM/BB1=OD/B1D
OM=BB1⋅OD/B1D=a/√6
Найдите расстояние между скрещивающимися диагональю куба и диагональю

Решение. Треугольник BB1D перпендикулярен AC. Отрезок OM ⊥ B1D, будет перпендикулярен и AC . OM - расстояние между AC и B1D.

к обеим прямым (единственный!)

Перпендикуляр от одной из прямых до параллельной

Перпендикуляр между параллельными плоскостями в которых лежат скрещивающиеся прямые, концы которого не обязательно лежат на прямых!

скрещивающейся прямой ?
Достаточно провести через одну из скрещивающихся прямых прямую

Заметим, что отрезок соединяющий точки пересечения пар параллельных прямых не равен расстоянию между скрещивающимися прямыми!

К этому типу относится уже рассмотренная задача о расстоянии между

Стандартный прием решения этих задач заключается в проведении плоскости, в которой лежит одна прямая, перпендикулярно другой скрещивающейся прямой

расстояние между прямыми AD и D1 M, где M –

Плоскость грани DD1C1C перпендикулярна ребру AD. Из точки D опустим перпендикуляр DK на D1 M. Треугольники DD1M и DKM подобны с коэффициентом подобия 1/2. DK=D1M/2=a⋅√5/2

M

K

расстояние между прямыми BD и O1 M, где M –

Диагональная плоскость AA1C1C перпендикулярна прямой BD. Из точки O опустим перпендикуляр OK на O1 M. Треугольники OO1M и OKM подобны. OK=OO1⋅OM/O1M =a/3 (по теореме Пифагора O1M=3/2√2, OM=1/2√2)

O1

K

M

O

Найдите расстояние между скрещивающимися диагоналями AC и A1 B смежных

Проведем диагональ D1C||A1B, получим треугольник AD1C||A1B, проведем диагональ A1C1||AC, получим треугольник A1BC1||AC

O1

K

M

O

M

N

Плоскости треугольников AD1C и A1BC1 параллельны и перпендикулярны плоскости BB1D1D

MN по теореме Фалеса равно 1/3 диагонали B1D: MN=a/√3



M
N
B
B1
D1
D
O1
O
Замечание. Перпендикулярность

в случае, если определены параллельные плоскости, в которых лежат прямые,

Для решения проблемы достаточно провести эту плоскость перпендикулярно к одной из прямых!

параллельную BM. Из точки B опустим на неё перпендикуляр BK.
A
B
C
M
D
K
N

По

Прямая BM находится на расстоянии BN от плоскости ADK, равном длине перпендикуляра BN к DK!

площадь DBK и длину DK.
SDBK =a2/4, DK=√5∙a/2, BN=2⋅ SDBK

обобщенный характер.
Если не проходят более элементарные приемы, то последний способ

A

B

M

D

Идея этого приема связана с двумя дополнительными объектами: а) плоскостью, в которой лежит одна из прямых. б) перпендикуляром к ней, через который проходит вторая прямая.

Запомните последнюю картинку!

прямой проводим прямую параллельно BM
A
B
M
D
Второй этап: из точки B опустим

E

K

Третий этап: в прямоугольном треугольнике DBK опустим перпендикуляр BN на DK. Его длина и будет равна расстоянию между прямыми AD и BM

N

ближайшие друг к другу?
Через точку N проводим прямую параллельно

A

B

M

D

E

K

Прямоугольный треугольник DBK переносим параллельно вдоль прямой на отрезок NL. Новые положения точек B и N будут ближайшими друг к другу точками прямых AD и BM

N

L

a=5 на ребрах AD и D1C взяты точки K и

M

K

E

H

N

Решение. Через точку E пересечения A1K c D1D проведем прямую || D1M. Из точки D1 на неё опустим перпендикуляр до пересечения в точке F. Высота D1N треугольника A1D1F и дает искомое расстояние.

F

A1F2=AD12+D1F2=25+25/3. A1F=10/√3. SA1D1F=25/(2√3). D1N=2⋅SH1D1F/A1F=25/10=5/2.
Оценка ответа на смысл. D1N=2,5