Софизмы 10 класс

Содержание

1. Софизмы 10 класс
2. Слайд 2
3. Софизмы появились еще в Древней Греции.
4. 1. «Число, равное другому числу, одновременно
5. 2.« Если “a” больше “b”, то “a”
6. отнимем от обеих его частей a·a,
7. Единица равна нулю Возьмем уравнение
8. Всякое число равно своему удвоенному значению Запишем
9. Слайд 9
10. Геометрические софизмы
11. Так как AD=FE=AB/2 и
12. или, иначе говоря Сумма
13. “Окружность имеет два центра” Построим произвольный угол
14. Мы поняли, что софистика-это целая наука,
15. Спасибо за внимание!
16. Скачать презентанцию

– (от греческого sophisma , «мастерство, умение, хитрая выдумка, уловка») - умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение,

Слайды и текст этой презентации

Слайд 1Тема: «Софизмы»
Работу выполнили ученицы 10 класса МОУ СОШ №103
Есаян Эльмирна

и Папоян Сатеник

Руководитель: Салова Татьяна Алексеевна

Слайд 2 –

(от греческого sophisma , «мастерство, умение, хитрая выдумка, уловка») -

умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям.

Софизм

Понятие "Софизм"

– (от греческого sophisma , «мастерство, умение, хитрая

Слайд 3 Софизмы появились еще в Древней Греции. Они тесно связаны

с философской деятельностью софистов — платных учителей мудрости, учивших всех

желающих философии, логике и, особенно, риторике (науке и искусству красноречия).

Экскурс в историю

Софизмы появились еще в Древней Греции. Они тесно связаны с философской деятельностью софистов — платных учителей

Слайд 4 1. «Число, равное другому числу, одновременно и больше, и

меньше его»
Возьмем два положительных равных числа a и

b и напишем для них следующие неравенства: a > - b

Перемножив получим неравенство a·b>b·b

Алгебраические софизмы

1. «Число, равное другому числу, одновременно и больше, и меньше его» Возьмем два положительных

Слайд 52.« Если “a” больше “b”, то “a” всегда больше, чем

“2b”»

Умножив это неравенство на b, получим новое неравенство

ab > b·b

Алгебраические софизмы

2.« Если “a” больше “b”, то “a” всегда больше, чем “2b”» Умножив это неравенство на

Слайд 6 отнимем от обеих его частей a·a,

получим неравенство ab-a·a > b·b - a·a, равносильное

a(b-a)> (b+a)(b-a) Разделим обе части неравенства на b-a получим a> b+a, прибавим к этому неравенству почленно исходное неравенство a > b имеем
2a >2b+a
откуда 2a >2b+a

Алгебраические софизмы

отнимем от обеих его частей a·a, получим неравенство ab-a·a > b·b - a·a,

Слайд 7Единица равна нулю
Возьмем уравнение

х-а = 0.

Разделив обе его части на х-а, получим
откуда сразу же получаем требуемое равенство
1=0.

Единица равна нулю Возьмем уравнение х-а =

Слайд 8Всякое число равно своему удвоенному значению
Запишем очевидное для любого

числа а тождество

а2-а2 = а2-а2.
Вынесем а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получив
а(а - а) = (а + а)(а - а).
Разделив обе части на а-а, получим а = а + а, или
а =2а.

Слайд 9

– это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.

Геометрические софизмы

Слайд 10Геометрические софизмы

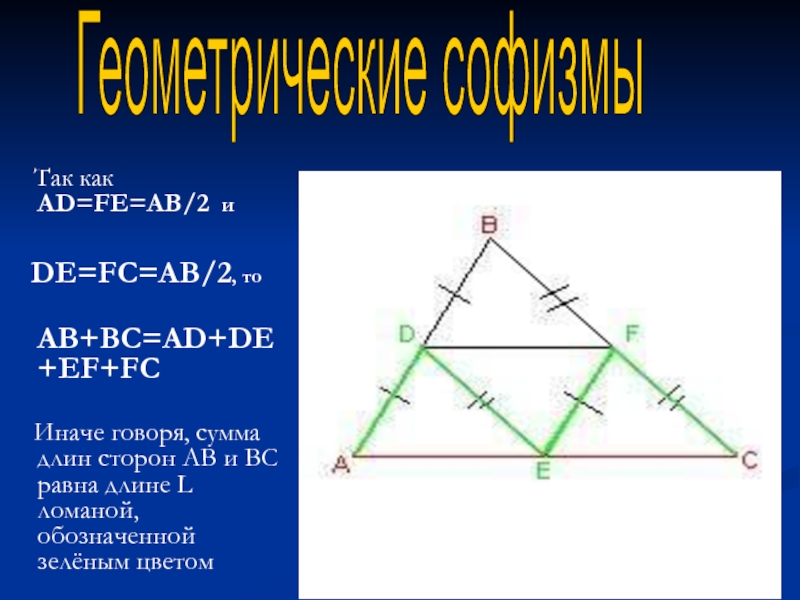
Слайд 11 Так как AD=FE=AB/2 и

DE=FC=AВ/2, то

AB+ВC=AD+DE+EF+FC

Иначе говоря, сумма

длин сторон AB и BC равна длине L ломаной, обозначенной зелёным цветом

Геометрические софизмы

Так как AD=FE=AB/2 и DE=FC=AВ/2, то AB+ВC=AD+DE+EF+FC Иначе

Слайд 12

или, иначе говоря
Сумма длин двух сторон

треугольника равна длине третьей стороны
Геометрические софизмы
L=AB+BC => AB+BC=AC

или, иначе говоря Сумма длин двух сторон треугольника равна длине третьей стороныГеометрические софизмыL=AB+BC =>

Слайд 13“Окружность имеет два центра”

Построим произвольный угол ABC и, взяв

на его сторонах две произвольные точки D и Е, восстановим

из них перпендикуляры к сторонам угла . Перпендикуляры эти должны пересечься (если бы они были параллельны, параллельны были бы и стороны АВ и СВ). Обозначим их точку пересечения буквой F.