Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические модели информационных потоков
Содержание
- 1. Математические модели информационных потоков
- 2. © ElVisti Моделирование информационныхпотоковБаланс темОбщий характер временной
- 3. © ElVisti Линейная модельВ некоторых случаях динамика
- 4. © ElVisti Примеры, для которых линейная модель
- 5. © ElVisti Экспоненциальная модельВ некоторых случаях процесс
- 6. © ElVisti Пример, для которого экспоненциальная модель
- 7. © ElVisti Логистическая модель Логистическую модель можно
- 8. © ElVisti Логистическая модель: примерыДинамика объемов публикаций
- 9. © ElVisti Логистическая модель: детализацияНа формальном уровне
- 10. © ElVisti Логистическая модель: уравненияПосле нормирования параметров
- 11. © ElVisti Логистическая модель: обобщенный график информационного потока
- 12. © ElVisti Спасибо за внимание!Ландэ Д.Вdwl@visti.nethttp://poiskbook.kiev.uaМЕЖДУНАРОДНЫЙ СОЛОМОНОВ УНИВЕРСИТЕТ Киев, Украина
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1© ElVisti
Лекция 6
“Математические модели
информационных потоков”
Дмитрий Владимирович ЛАНДЭ
МЕЖДУНАРОДНЫЙ СОЛОМОНОВ
УНИВЕРСИТЕТ
Слайд 2© ElVisti
Моделирование информационных
потоков
Баланс тем
Общий характер временной зависимости числа тематических
публикаций в сети определяется закономерностями, которые целиком допускают построение математических
моделей.Модель, аналогичная модели Бартона-Кеблера, учитывает статическую и динамическую составляющие от общих объемов сообщений по заданной тематике с учетом старения информации:
v(T) = 1 – ae-T – be-2T.
Организации-генераторы новостной информации в производят поток информации, в среднем постоянный по количеству сообщений. Изменяются во времени лишь объемы сообщений, которые соответствуют той или другой теме. Таким образом, рост количества публикаций по одной теме сопровождается уменьшением публикаций по другим темам:
где ni(t) – количество публикаций в единицу времени, а M – общее количество всех возможных тем.
Слайд 3© ElVisti
Линейная модель
В некоторых случаях динамика тематических информационных потоков
реализуется линейно, то есть количество сообщений в момент времени t
можно представить формулой:y(t) = y(t0) + v(t - t0),
где y(t) – количество сообщений на время t, v – середняя скорость увеличения (уменьшения) интенсивности тематического информационного потока во времени.
Содержательная составляющая информационного потока может быть оценена как флюктуация информационного потока – изменение стандартного отклонения σ(t):
В случае поведения стандартного отклонения σ(t) ∝ tμ, то чем большее значение μ, тем выше корреляция между текущими и предыдущими сообщениями. В этих случаях μ характеризует степень связи между случайными событиями и принимает значение от ½ до 1.
Слайд 4© ElVisti
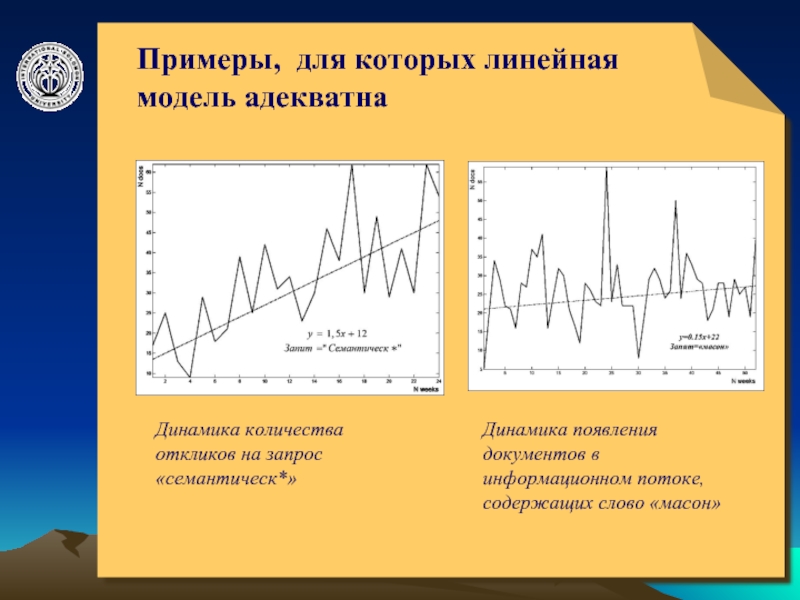
Примеры, для которых линейная модель адекватна
Динамика количества откликов
на запрос «семантическ*»
Динамика появления документов в информационном потоке, содержащих
слово «масон»Слайд 5© ElVisti
Экспоненциальная модель
В некоторых случаях процесс увеличения (роста) актуальности
или старения информации описывается экспоненциальной зависимостью, которую можно аппроксимировать такой
формулой:N(t) = N(t0)eλ(t - to) ,
где λ - среднее относительное изменение интенсивности информационного потока.
Относительное изменение интенсивности в определенный момент времени исчисляется по формуле:
λ(ti)=(N(ti) – N(ti-1))/N(ti-1).
Изменение флюктуаций величины λ(ti) относительно среднего значения может быть оценена по формуле:
Если σ(t) изменяется как корень квадратный из времени, то можно говорить о процессе с независимыми приращениями. В случае наличия значительной доли зависимых сообщений справедливо: σ(t)∝ tμ, причем μ < 1. Значение μ >> ½, говорит о наличии долгосрочной памяти системы.
Слайд 6© ElVisti
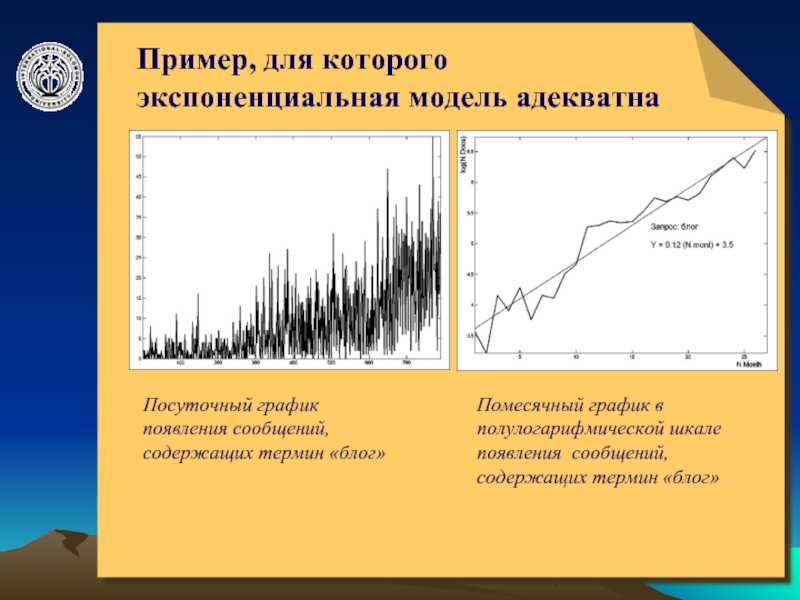
Пример, для которого экспоненциальная модель адекватна
Посуточный график появления
сообщений, содержащих термин «блог»
Помесячный график в полулогарифмической шкале появления
сообщений, содержащих термин «блог»Слайд 7© ElVisti
Логистическая модель
Логистическую модель можно рассматривать как обобщение
экспоненциальной модели Мальтуса, которая, предусматривает пропорциональность скорости роста функции ее
значения в каждый момент времени:где k – некоторый коэффициент.
В случае логистической модели идея заключается в том, чтобы сделать коэффициент в уравнении Мальтуса функцией времени. Наиболее распространенным есть использования константы, которая в явном виде ограничивает рост решения. В нашем случае с этой целью используем емкость N. Тогда правая часть соответствующего выражения представляется в виде:
где k – коэффициент Мальтуса, а r – коэффициент, который описывает отрицательные для данной системы процессы, связанные с внутренними факторами.
Слайд 8© ElVisti
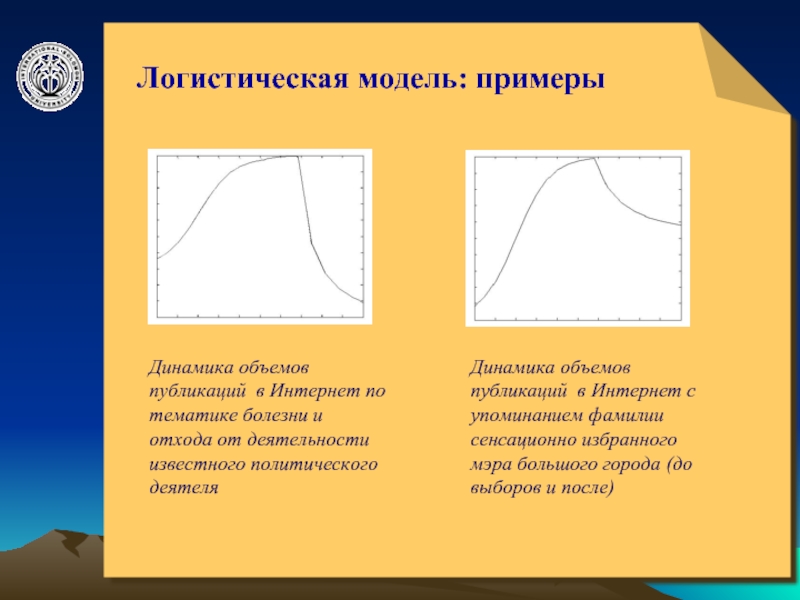
Логистическая модель: примеры
Динамика объемов публикаций в Интернет по
тематике болезни и отхода от деятельности известного политического деятеля
Динамика
объемов публикаций в Интернет с упоминанием фамилии сенсационно избранного мэра большого города (до выборов и после)Слайд 9© ElVisti
Логистическая модель: детализация
На формальном уровне сопоставим с темой
два параметра: продолжительность (характерное “время жизни”) λ и интенсивность D.
Продолжительность - промежуток времени, в течение которого тема имеет выраженную актуальность. Интенсивность - величина, которая характеризует порожденное соответствующей темой количество публикаций, усредненное по промежутку λ.
Вклад интенсивности D определяется следующим образом:
Соответственно, рассматриваются две временные области:
0 < t ≤ λ с D > 0 и t > λ с D = 0, для которых решениями являются функции u(t) и v(t). Полное решение получается путем “сшивки” на границе в точке λ:
Слайд 10© ElVisti
Логистическая модель: уравнения
После нормирования параметров пороговой величины N,
уравнение для первой области имеет вид:
Решение этого уравнения:
Уравнение для
второй области имеет вид: Решение второго уравнения: