Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисления площадей геометрических фигур. Метод Монте-Карло.
Содержание
- 1. Вычисления площадей геометрических фигур. Метод Монте-Карло.
- 2. Цель работы: освоить понятие метода Монте-Карло, как
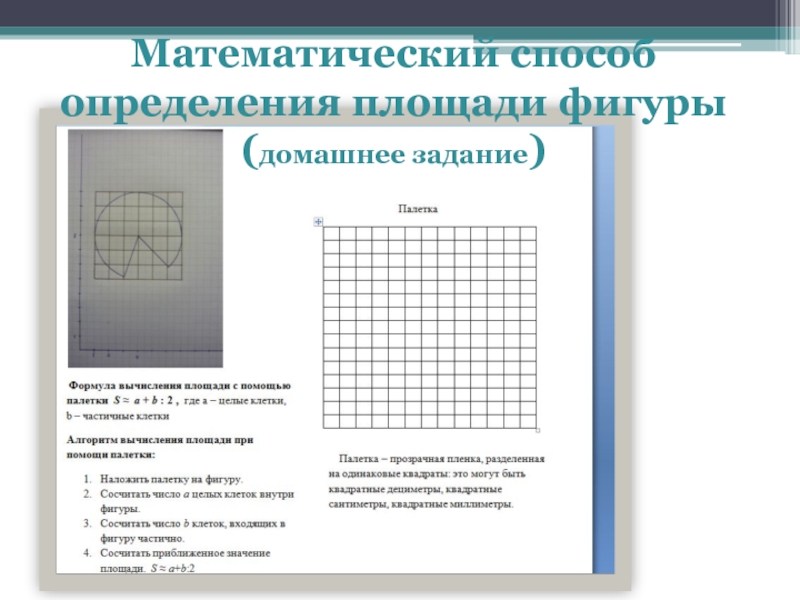
- 3. Математический способ определения площади фигуры (домашнее задание)
- 4. Вписываем сложную фигуру в другую фигуру, для
- 5. Фигура ограничена тремя границами:y >= 3x-4 –
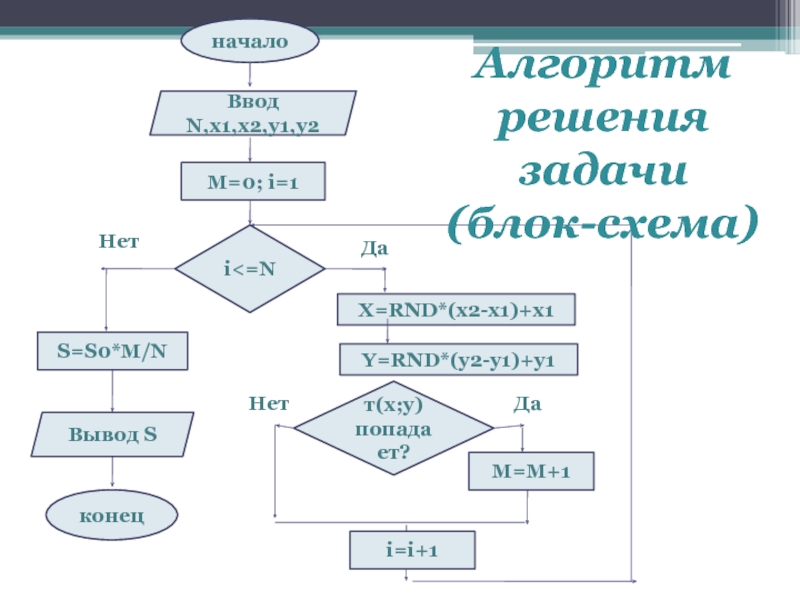
- 6. началоВвод N,x1,x2,y1,y2 M=0; i=1i
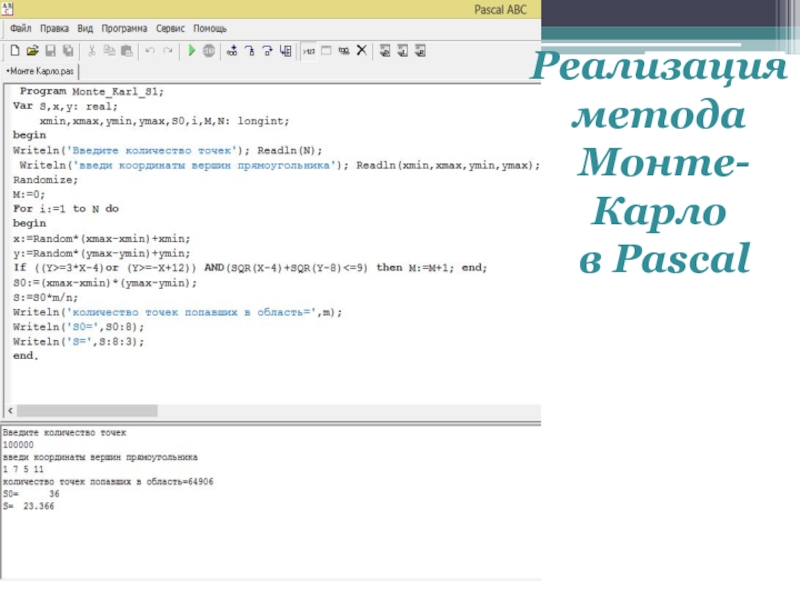
- 7. Реализация метода Монте-Карло в Pascal
- 8. Решение задачи в ExcelВ Excel с помощью
- 9. Число точек, попавших внутрь фигуры или на
- 10. Решение задачи в Excelнужными формулами необходимо заполнить
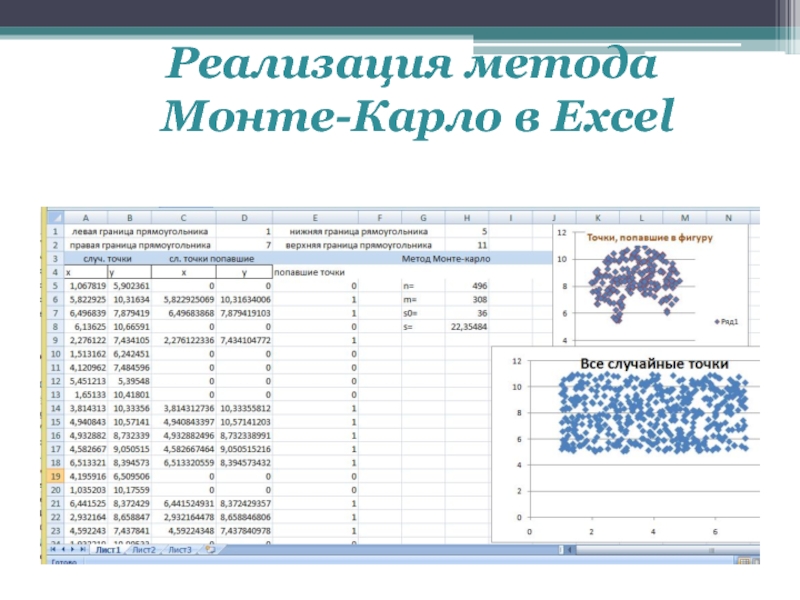
- 11. Реализация метода Монте-Карло в Excel
- 12. Принципиальная особенность метода состоит в том,
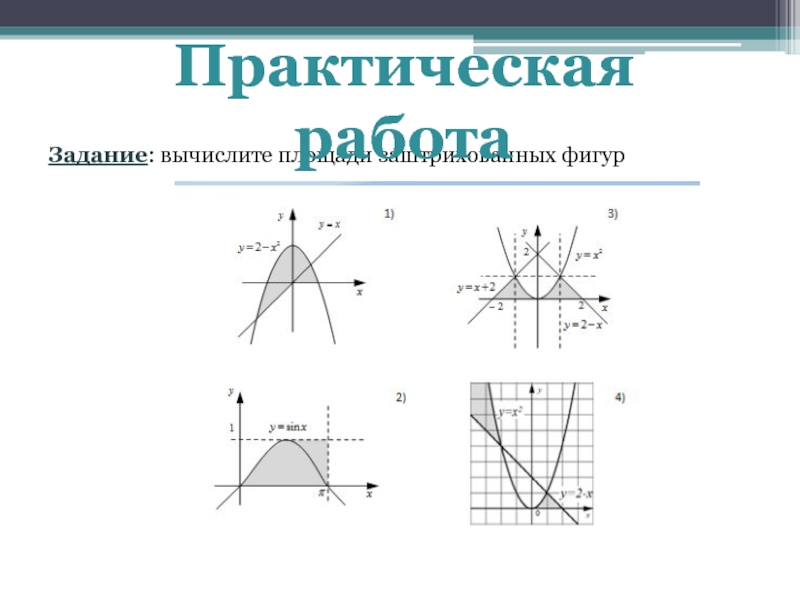
- 13. Задание: вычислите площади заштрихованных фигурПрактическая работа
- 14. А.Г. Гейн, В.Г.Житомирский, Е.В.Линецкий, М.В.Сапир, «Основы информатики
- 15. Скачать презентанцию
Цель работы: освоить понятие метода Монте-Карло, как основного метода создания вероятностных моделей; Задачи:Научиться вычислять площади нестандартных фигур используя среду программирования Pascal и электронные таблицы Excel;уметь записывать предикат для фигуры, площадь которой
Слайды и текст этой презентации
Слайд 1Тема:
Раздел: Моделирование
Различные способы вычисления
площадей геометрических
фигур
Автор: Розова Е.Е.,
учитель информатики МОУ гимназии№3 им. А.Н.Островского г. Кинешма, Ивановской обл.
Слайд 2Цель работы: освоить понятие метода Монте-Карло, как основного метода создания
вероятностных моделей;
Задачи:
Научиться вычислять площади нестандартных фигур используя среду программирования Pascal
и электронные таблицы Excel;уметь записывать предикат для фигуры, площадь которой необходимо найти
Сравнить полученные результаты;
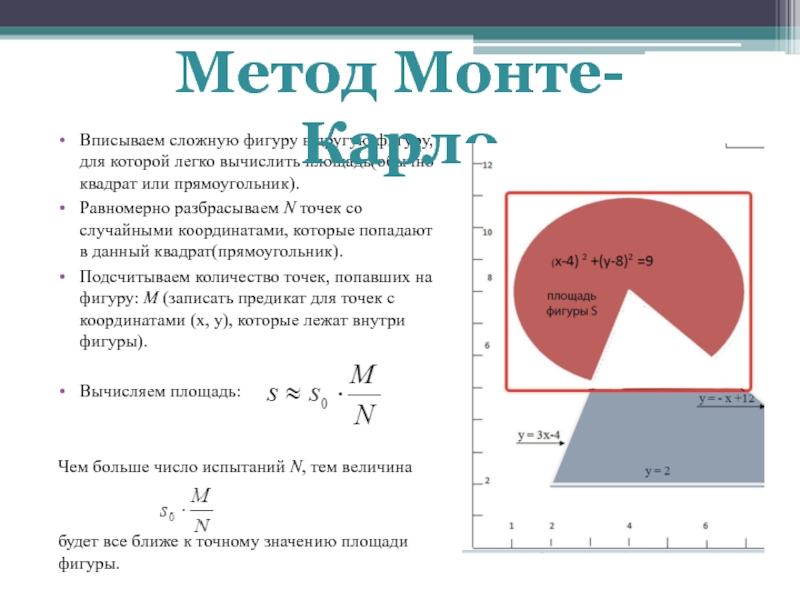
Слайд 4Вписываем сложную фигуру в другую фигуру, для которой легко вычислить
площадь(обычно квадрат или прямоугольник).
Равномерно разбрасываем N точек со случайными
координатами, которые попадают в данный квадрат(прямоугольник).Подсчитываем количество точек, попавших на фигуру: M (записать предикат для точек с координатами (x, y), которые лежат внутри фигуры).
Вычисляем площадь:
Чем больше число испытаний N, тем величина
будет все ближе к точному значению площади фигуры.
Метод Монте-Карло
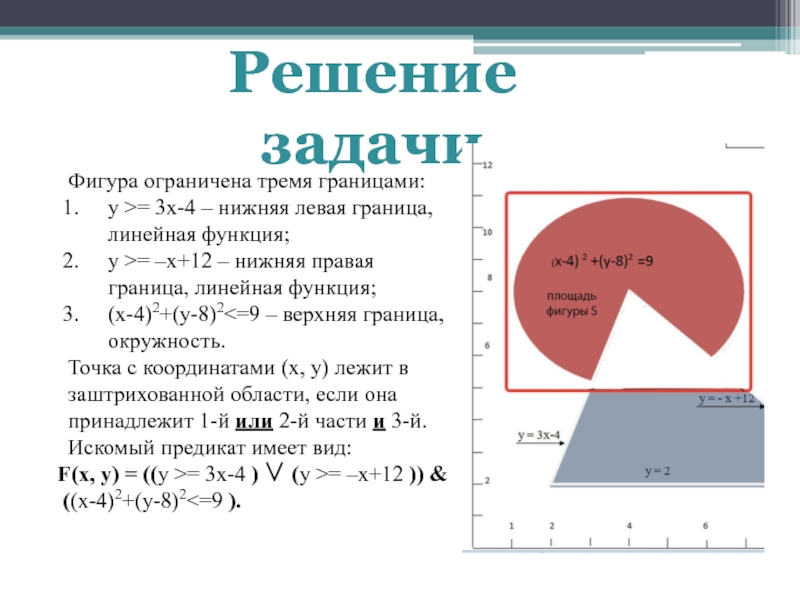
Слайд 5Фигура ограничена тремя границами:
y >= 3x-4 – нижняя левая граница,
линейная функция;
y >= –x+12 – нижняя правая граница, линейная функция;
(x-4)2+(y-8)2
– верхняя граница, окружность.Точка с координатами (x, y) лежит в заштрихованной области, если она принадлежит 1-й или 2-й части и 3-й.
Искомый предикат имеет вид:
F(x, y) = ((y >= 3x-4 ) (y >= –x+12 )) &
((x-4)2+(y-8)2<=9 ).
Решение задачи
Слайд 8Решение задачи в Excel
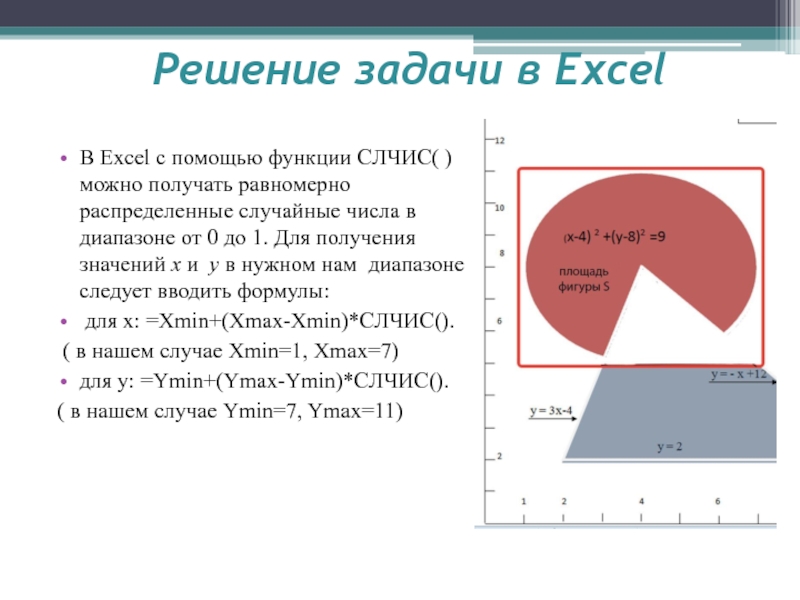
В Excel с помощью функции СЛЧИС( )
можно получать равномерно распределенные случайные числа в диапазоне от 0
до 1. Для получения значений x и y в нужном нам диапазоне следует вводить формулы:для x: =Xmin+(Xmax-Xmin)*СЛЧИС().
( в нашем случае Xmin=1, Xmax=7)
для y: =Ymin+(Ymax-Ymin)*СЛЧИС().
( в нашем случае Ymin=7, Ymax=11)
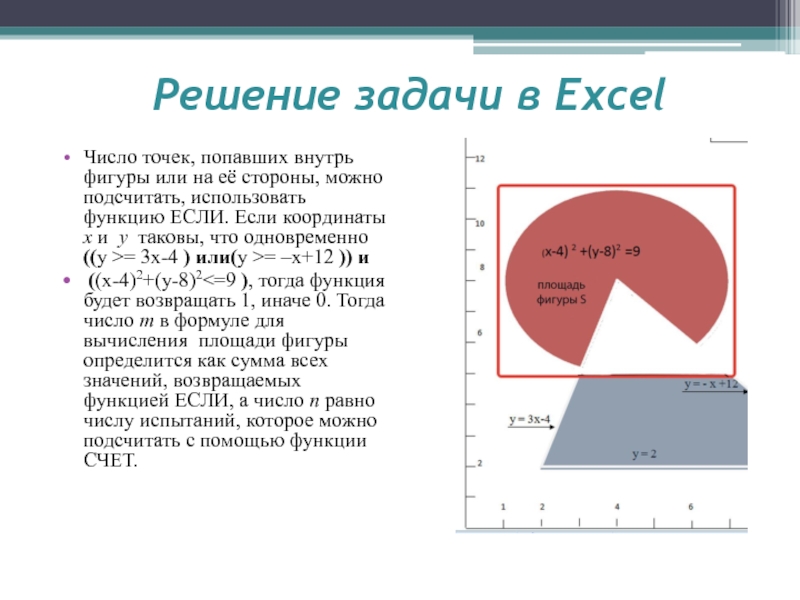
Слайд 9Число точек, попавших внутрь фигуры или на её стороны, можно
подсчитать, использовать функцию ЕСЛИ. Если координаты x и y таковы,
что одновременно ((y >= 3x-4 ) или(y >= –x+12 )) и((x-4)2+(y-8)2<=9 ), тогда функция будет возвращать 1, иначе 0. Тогда число m в формуле для вычисления площади фигуры определится как сумма всех значений, возвращаемых функцией ЕСЛИ, а число n равно числу испытаний, которое можно подсчитать с помощью функции СЧЕТ.
Решение задачи в Excel
Слайд 10Решение задачи в Excel
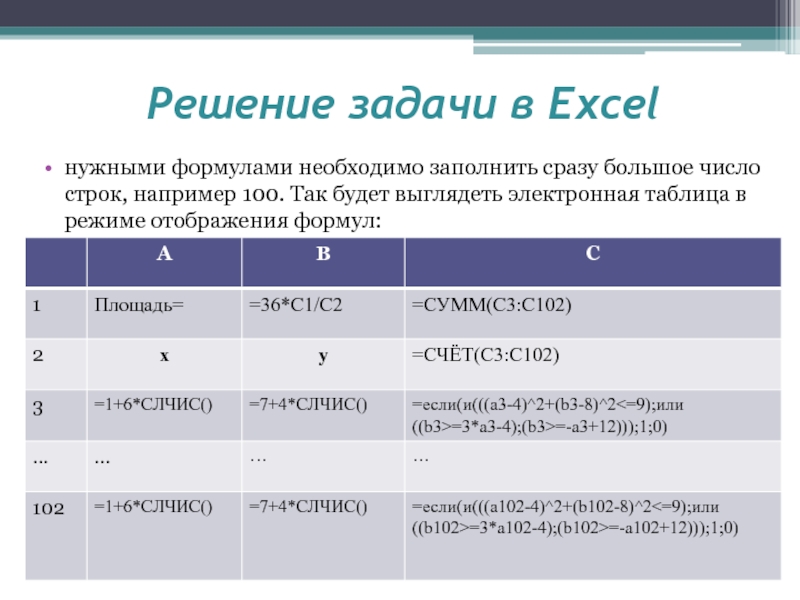
нужными формулами необходимо заполнить сразу большое число
строк, например 100. Так будет выглядеть электронная таблица в режиме
отображения формул:Слайд 12
Принципиальная особенность метода состоит в том, что он гарантирует
высокое качество статистических оценок только при весьма большом числе испытаний,
которое невозможно выполнить без помощи компьютераТабличные процессоры не очень удобны для проведения расчетов Монте-Карло(много времени занимает копирование формул для большого количества случайных точек), однако с их использованием можно достаточно просто проиллюстрировать основные особенности этого метода
Выводы:
Слайд 14А.Г. Гейн, В.Г.Житомирский, Е.В.Линецкий, М.В.Сапир, «Основы информатики и вычислительной техники»
Москва, «Просвещение», 1993г;
3. Ермаков С.М. «Методы Монте-Карло и смежные вопросы»,
Москва, Наука, 1971г;4. Математика. Большой Энциклопедический Словарь гл. редактор Ю.В.Прохоров, Москва, Большая Российская Энциклопедия
Источники информации: