Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Булевы функции
Содержание
- 1. Булевы функции
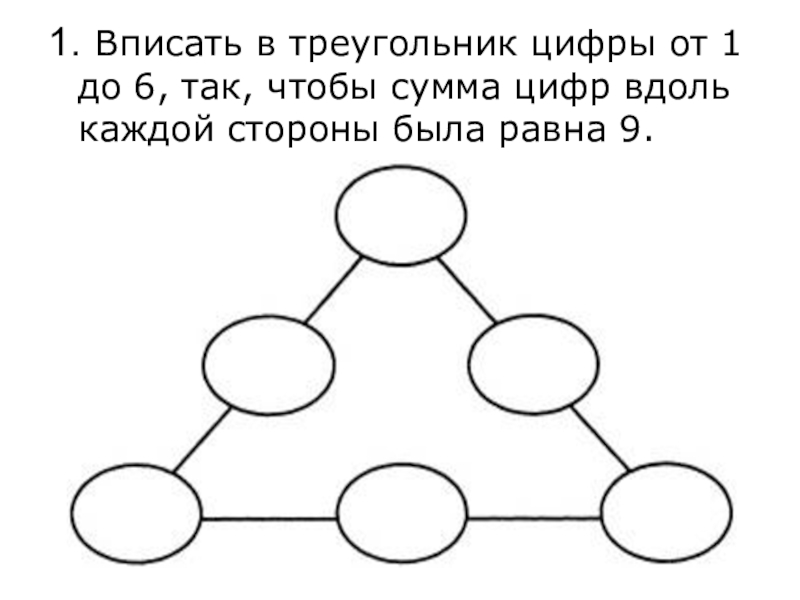
- 2. 1. Вписать в треугольник цифры от 1
- 3. 2. В авиационном подразделении служат Потапов,
- 4. 3. В компании 5 человек: Алексей, Вера,
- 5. 1. В течение последних четырёх лет Евгений,
- 6. 2. В поезде Москва-Санкт-Петербург едутпассажиры. Иванов, Петров
- 7. План занятия:Изучение теоретического материала.2. Практическая работа.3. Самостоятельная работа.Раздел 1. Алгебра высказываний Тема 1.2.3.Истинностные (булевы) функции
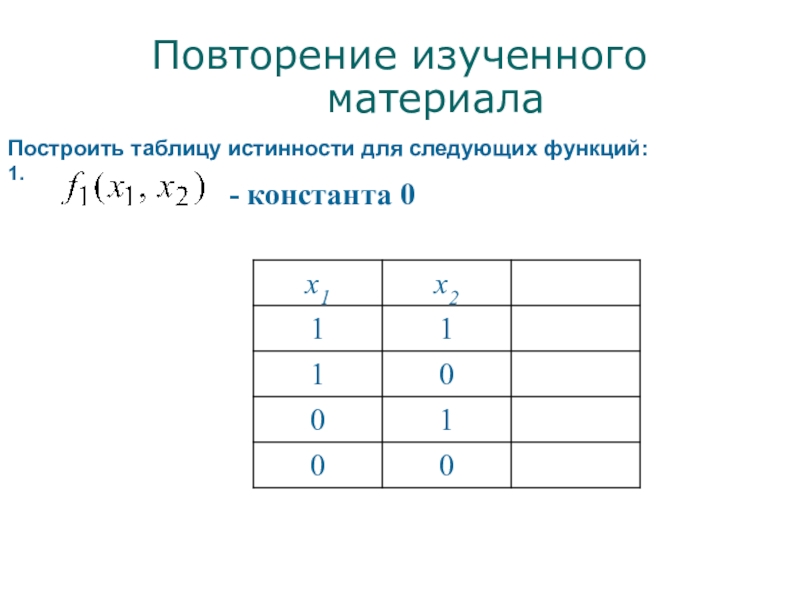
- 8. Повторение изученного материалаПостроить таблицу истинности для следующих функций:1. - константа 0
- 9. Повторение изученного материалаПостроить таблицу истинности для следующих функций:2. - штрих Шеффера
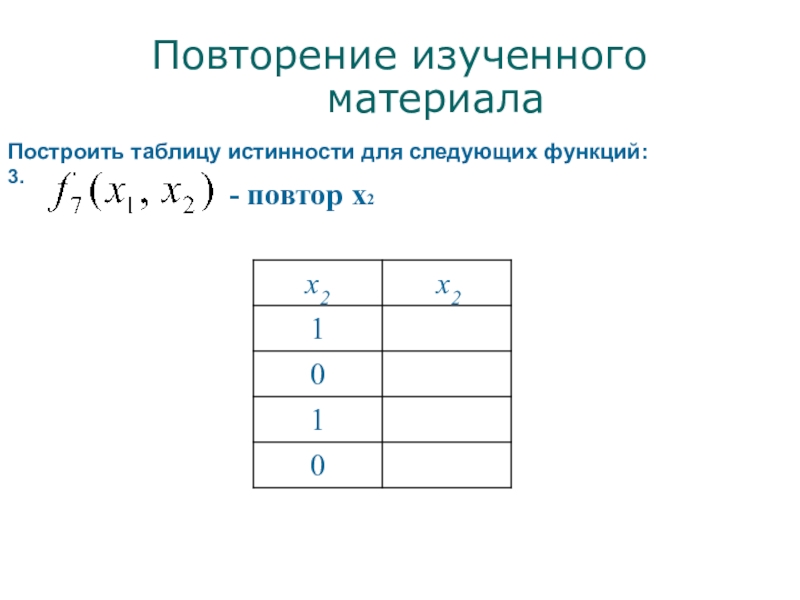
- 10. Повторение изученного материалаПостроить таблицу истинности для следующих функций:3. - повтор x2
- 11. Повторение изученного материалаПостроить таблицу истинности для следующих функций:4. - стрелка Пирса
- 12. Повторение изученного материалаПостроить таблицу истинности для следующих функций:5. -правая импликация
- 13. Повторение изученного материалаПостроить таблицу истинности для следующих функций:6. - левая импликация
- 14. Повторение изученного материалаПостроить таблицу истинности для следующих функций:7. -запрет -запрет
- 15. Повторение изученного материалаПостроить таблицу истинности для следующих функций:8. - эквивалентность
- 16. Повторение изученного материалаЧерез какие логические операцииможно выразить штрих Шеффера истрелку Пирса(штрих Лукасевича)?
- 17. Проверочная работа «Булевы функции двух переменных»1. Построить таблицы истинности следующих функций:
- 18. Проверочная работа «Булевы функции двух переменных»2. Построить таблицы истинности следующих функций:
- 19. СДНФ и СКНФ.
- 20. Функция алгебры логикиФункцией алгебры логики n называетсялюбая
- 21. Правила построения СДНФ.
- 22. Для формулы получаем любую ДНФ.Из ДНФ получаем
- 23. 2. Из ДНФ получаем СДНФ с
- 24. Правила построения СКНФ.
- 25. Для формулы получаем любую КНФ.Из КНФ получаем
- 26. 2. Из КНФ получаем СКНФ с
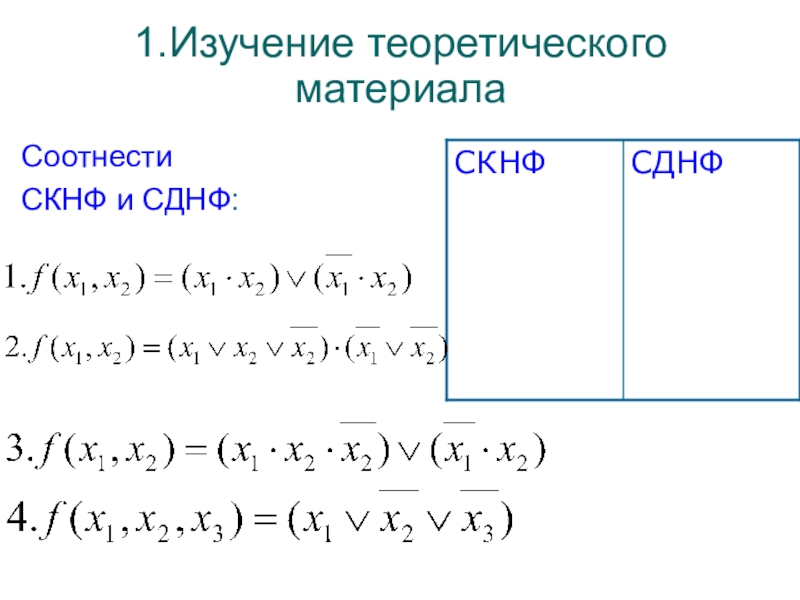
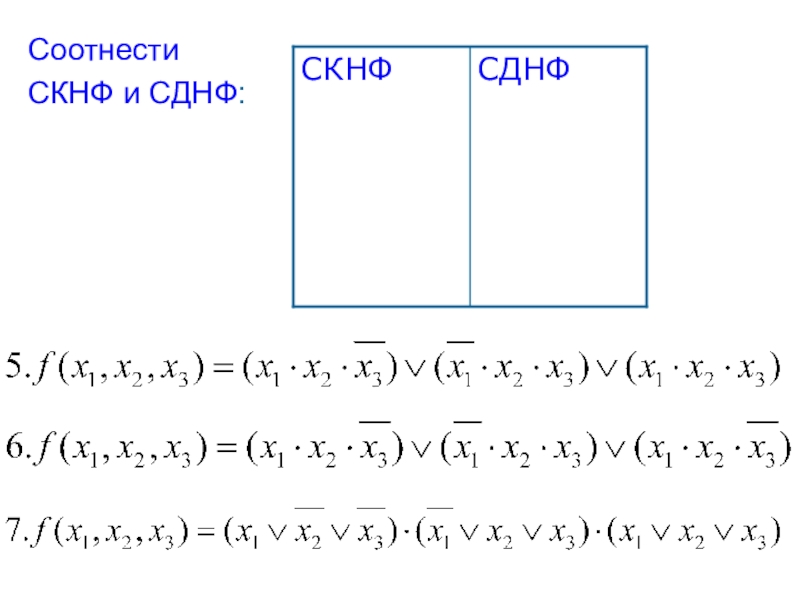
- 27. 1.Изучение теоретического материалаСоотнести СКНФ и СДНФ:
- 28. Соотнести СКНФ и СДНФ:
- 29. 2. Практическая работа 1. Формулу привести к
- 30. Построение СДНФ и СКНФ.Задание № 1:Приведите равносильнымипреобразованиями
- 31. Задание №2:Найти формулу, определяющую функцию
- 32. Построить таблицу истинности для булевых функций трёх переменных: 3. Самостоятельная работа
- 33. 2. Проверьте, являются ли булевы функции эквивалентными./построение
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 21. Вписать в треугольник цифры от 1 до 6, так,
чтобы сумма цифр вдоль каждой стороны была равна 9.
Слайд 32. В авиационном подразделении служат Потапов, Щедрин, Семёнов, Коновалов
и Самойлов. Их специальности: пилот, штурман, бортмеханик, радист и синоптик.
Известно:
Щедрин и Коновалов незнакомы с управлением самолёта;
Потапов и Коновалов готовятся стать штурманами;
Квартиры Щедрина и Самойлова находятся рядом с квартирой радиста;
Семёнов, находясь в доме отдыха, встретил Щедрина и сестру синоптика;
Потапов и Щедрин в свободное время играют в шахматы с бортмехаником и пилотом;
Коновалов, Семёнов и синоптик увлекаются боксом;
Радист боксом не увлекается.
Определить, какую специальность имеет каждый из них?
Щедрин- штурман, Коновалов-бортмеханик,Семёнов-пилот,
Самойлов-синоптик,Потапов-радист.
Слайд 43. В компании 5 человек: Алексей, Вера, Глеб, Даша и
Евгений. На вечеринку:
Если пригласить Алексея, то необходимо пригласить и Веру;
Можно
пригласить либо Глеба, либо Веру, но не вместе;Можно пригласить либо Дашу, либо Евгения, либо их обоих;
Дашу можно пригласить либо вместе с Глебом, либо ни того, ни другого;
Если пригласить Евгения, то тогда необходимо пригласить Алексея и Дашу.
Кого все-таки пригласить на вечеринку?
Пригласить нужно Дашу и Глеба.
Слайд 51. В течение последних четырёх лет Евгений, Фёдор, Дмитрий и
Борис, работающие на одном предприятии, получали отпуск в мае, июне,
июле и августе. Время их отпусков не совпадало и ни один из них не получил отпуска в один и тот же месяц.В первый год Дмитрий отдыхал в июле, а второй- в августе.
Во второй год в мае получил Евгений.
На третий год в июне отпуск получил Борис, а на четвёртый год в июле отдыхал Фёдор.
В каком месяце отдыхал Евгений в первый год?
В первый год Евгений отдыхал в июне.
Слайд 62. В поезде Москва-Санкт-Петербург едут
пассажиры. Иванов, Петров и Сидоров. Такие
же фамилии имеют машинист, помощник
машиниста и бригадир поезда. Известно, что
пассажир
Иванов живёт в Москве, бригадир поездаживёт на полпути от Москвы до Санкт- Петербурга;
пассажир-однофамилец бригадира поезда живёт в
Санкт-Петербурге; тот пассажир, который живёт
ближе к месту жительства бригадира, чем
другие пассажиры, зарабатывает в месяц
ровно втрое больше бригадира; пассажир
Петров зарабатывает в месяц 20.000 рублей;
Сидоров(из бригады) недавно выиграл у
помощника машиниста партию на бильярде.
Как фамилия машиниста?
Машинист-Сидоров, помощник-Иванов, бригадир-Петров
Слайд 7План занятия:
Изучение теоретического материала.
2. Практическая работа.
3. Самостоятельная работа.
Раздел 1. Алгебра
высказываний
Тема 1.2.3.Истинностные (булевы) функции
Слайд 8Повторение изученного материала
Построить таблицу истинности для следующих функций:
1.
-
константа 0
Слайд 9Повторение изученного материала
Построить таблицу истинности для следующих функций:
2.
-
штрих Шеффера
Слайд 10Повторение изученного материала
Построить таблицу истинности для следующих функций:
3.
-
повтор x2
Слайд 11Повторение изученного материала
Построить таблицу истинности для следующих функций:
4.
-
стрелка Пирса
Слайд 12Повторение изученного материала
Построить таблицу истинности для следующих функций:
5.
-правая
импликация
Слайд 13Повторение изученного материала
Построить таблицу истинности для следующих функций:
6.
-
левая импликация
Слайд 14Повторение изученного материала
Построить таблицу истинности для следующих функций:
7.
-запрет
-запрет
Слайд 15Повторение изученного материала
Построить таблицу истинности для следующих функций:
8.
-
эквивалентность
Слайд 16Повторение изученного материала
Через какие логические операции
можно выразить штрих Шеффера и
стрелку
Пирса(штрих Лукасевича)?
Слайд 17Проверочная работа
«Булевы функции двух переменных»
1. Построить таблицы истинности следующих
функций:
Слайд 18Проверочная работа
«Булевы функции двух переменных»
2. Построить таблицы истинности следующих
функций:
Слайд 20Функция алгебры логики
Функцией алгебры логики n называется
любая функция n переменных
аргументы которой принимают два
значения 0 и 1,
а сама функция
принимает одно из двухзначений 1 или 0.
Слайд 22Для формулы получаем любую ДНФ.
Из ДНФ получаем СДНФ с помощью:
Пусть
В есть слагаемое ДНФ, не содержащее xi. Тогда надо заменить
В на слагаемоеЕсли в ДНФ есть два одинаковых слагаемых В и В, то одно отбросить, т. к.
Слайд 232. Из ДНФ получаем СДНФ с помощью:
3) Если
в ДНФ есть
,то его отбросить.
4) Если в некоторое слагаемое В переменная
входит дважды, то лишнюю отбросить, т. к.
Слайд 25Для формулы получаем любую КНФ.
Из КНФ получаем СКНФ с помощью:
Пусть
В есть слагаемое КНФ, не содержащее xi. Тогда надо заменить
В на слагаемоеЕсли в КНФ есть два одинаковых слагаемых В и В, то одно отбросить, т. к.
Слайд 262. Из КНФ получаем СКНФ с помощью:
3) Если
в КНФ есть
,то его отбросить.
4) Если в некоторое слагаемое В переменная
входит дважды, то лишнюю отбросить, т. к.
Слайд 292. Практическая работа
1. Формулу привести к СДНФ, предварительно приведя её
к ДНФ равносильными преобразованиями.
2. Для примера 1 найти СДНФ путем
оставления таблицы истинности.3. Для формулы из примера 1 найти СКНФ, предварительно приведя её к КНФ равносильными преобразованиями.
4. Для формулы из примера 1 найти СКНФ, записав предварительно СДНФ её отрицания, а потом воспользовавшись формулой.
Слайд 30Построение СДНФ и СКНФ.
Задание № 1:
Приведите равносильными
преобразованиями формулу своего
варианта к
СДНФ и
проверьте получившийся результат с
помощью таблиц истинности.
Слайд 33
2. Проверьте, являются ли булевы функции эквивалентными.
/построение таблицы истинности или
упрощение с помощью равносильностей/.
3. По заданной функции постройте таблицу истинности,
приведите функцию к СКНФ (СДНФ)./ использовать алгоритм построения
СКНФ, СДНФ/.
3.Самостоятельная работа