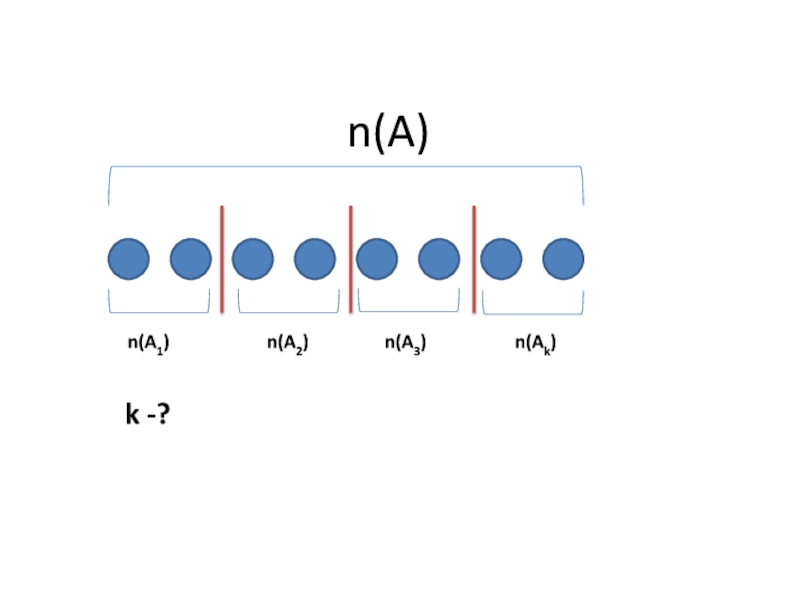
следующим образом:
пусть a = n(A) и
множество A разбито на попарно непересекающиеся равномощные подмножества.Если b – число подмножеств в разбиении множества A, то частным чисел a и b называется число элементов каждого подмножества.