Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества
Содержание
- 1. Множества
- 2. Определение Множество – это совокупность однородных предметов
- 3. Определение Объекты, из которых состоит множество, называются
- 4. Определение Множество, не содержащее ни
- 5. Способы описания элементов множества: Перечисление;С помощью характеристического свойства.
- 6. Слайд 6
- 7. Опишите элементы множествB={x | xϵN, 7 ≤
- 8. Запомнить!N - множество натуральных чисел,Zₒ - множество
- 9. Классификация множествØ – пустое множествоА = {а}
- 10. ОпределениеМножество, состоящее из конечного числа элементов, называется конечным.Остальные множества называются бесконечными.
- 11. Задать множества с помощью характеристических свойствА –
- 12. Определение Множества А и В называют
- 13. Дать характеристику множеству А = { понедельник,
- 14. Определение Множество В называют подмножеством
- 15. ОпределенияМножество А называется числовым, если его элементами
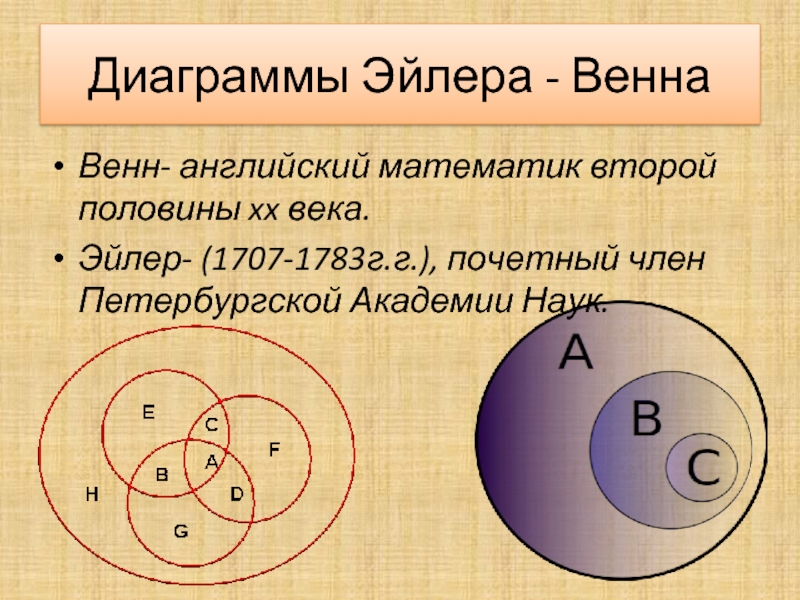
- 16. Диаграммы Эйлера - ВеннаВенн- английский математик второй половины xx века.Эйлер- (1707-1783г.г.), почетный член Петербургской Академии Наук.
- 17. Слайд 17
- 18. Скачать презентанцию
Определение Множество – это совокупность однородных предметов любой природы.Множество книг данной библиотекиМножество всех вершин данного треугольникаМножество всех натуральных чисел Множество все точек данной прямой и т. д.
Слайды и текст этой презентации
Слайд 1Множество-основное понятие курса математики
Работу выполнила: учитель математики МБОУ Сергиевская СОШ
Калинина Елена Петровна
Слайд 2Определение
Множество – это совокупность однородных предметов любой природы.
Множество книг
данной библиотеки
Множество всех вершин данного треугольника
Множество всех натуральных чисел
Множество
все точек данной прямой и т. д.Слайд 3Определение
Объекты, из которых состоит множество, называются его элементами.
Множества -
А, В, С, D, Е ….
Элементы – а, b, с,
d, e…..а ϵ А – « а принадлежит множеству А» или « а является элементом множества А»
а ϵ А – «а не принадлежит множеству А» или « а не является элементом множества А»
Слайд 4Определение
Множество, не содержащее ни одного элемента, называется
пустым множеством и обозначается Ø.
Например: множество чисел, кратных
0.Слайд 7Опишите элементы множеств
B={x | xϵN, 7 ≤ x ≤ 10
}
Ответ: множество натуральных чисел от 7 до 10 включительно.
С={
x | xϵZ ₊ }Ответ: множество целых положительных чисел.
Слайд 8Запомнить!
N - множество натуральных чисел,
Zₒ - множество целых неотрицательных чисел,
Z
- множество целых чисел,
Q - множество рациональных чисел.
Слайд 9Классификация множеств
Ø – пустое множество
А = {а} – одноэлементное множество
В
= {a, b, c, d } – конечное множество
N =
{1,2,3,4..} – бесконечное множество натуральных чисел.Слайд 10 Определение
Множество, состоящее из конечного числа элементов, называется конечным.
Остальные множества
называются бесконечными.
Слайд 11Задать множества с помощью характеристических свойств
А – множество двузначных чисел,
записанных одинаковыми цифрами
А = {11,22, 33,44,55,66,77,88,99}
В – множество двузначных чисел,
делящихся на 11В = {11,22,33,44,55,66,77,88,99}
Слайд 12Определение
Множества А и В называют равными, если они
состоят из одних и тех же элементов.
Пишут:
А=В Слайд 13Дать характеристику множеству
А = { понедельник, вторник, среда, четверг,
пятница, суббота, воскресенье}
Ответ: множество дней недели.
В = {понедельник, пятница}
Ответ:
множество дней недели, название которых начинается с буквы П.Слайд 14Определение
Множество В называют подмножеством множества А, если
каждый элемент из множества В является элементом множества А.
В ϲ А ( ϲ – знак включения)Читают:
В- подмножество А;
А содержит В
Слайд 15Определения
Множество А называется числовым, если его элементами являются числа.
Множество А
называется точечным, если его элементами являются точки.
Геометрической фигурой называется всякое
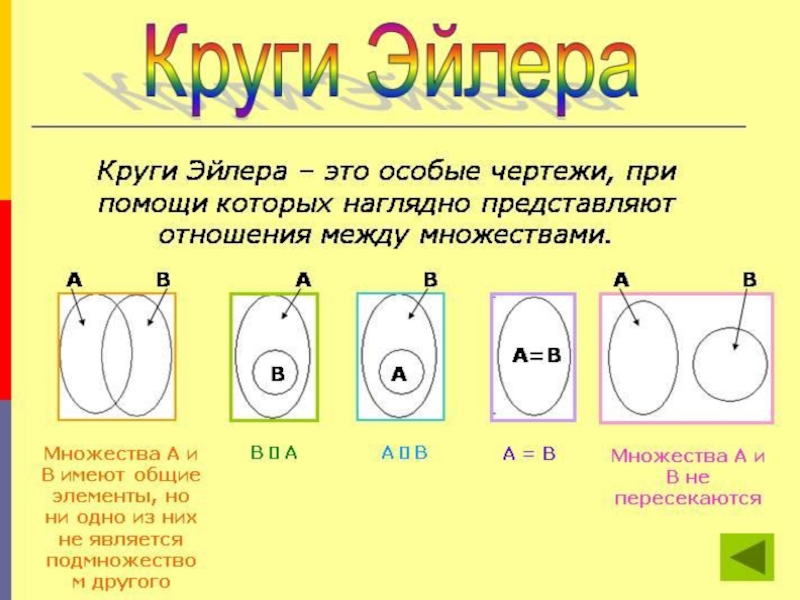
множество точек.Слайд 16Диаграммы Эйлера - Венна
Венн- английский математик второй половины xx века.
Эйлер-
(1707-1783г.г.), почетный член Петербургской Академии Наук.
Теги