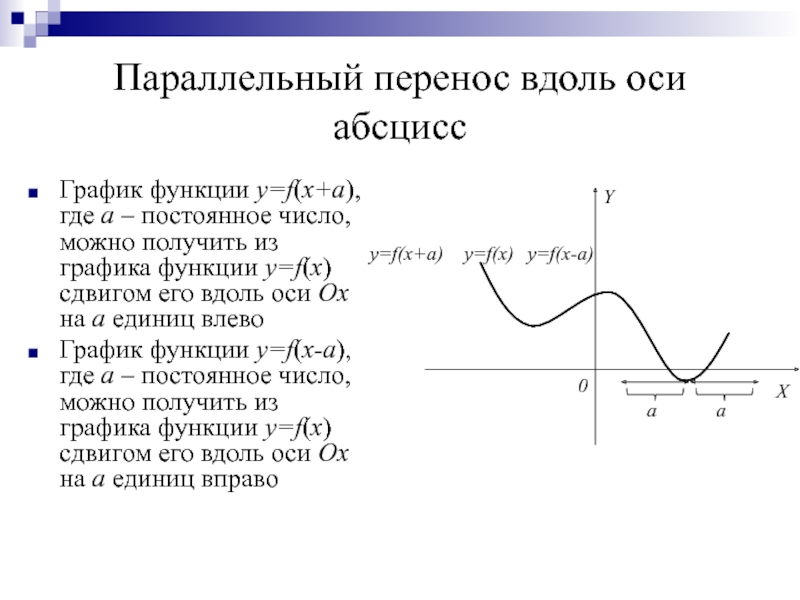
постоянное число, получается из графика y=f(x) смещением его вдоль оси
Oy на a единиц вверх, если a>0График функции y=f(x)-a, где a – постоянное число, получается из графика y=f(x) смещением его вдоль оси Oy на a единиц вниз, если a<0
X
Y
0
y=f(x)
y=f(x)+a
y=f(x)-a
a
a